Содержание
- 2. Это утверждение непосредственно следует из определения 6 и теоремы 2.3.
- 3. Примеры. Таким образом, циклическая группа, порождённая матрицей А, имеет порядок 2. Таким образом, теперь подгруппа, порождённая
- 4. 8. –
- 6. (1) Разделим с остатком k на n: k = nt + r, 0 ≤ r
- 7. Доказательство. Разделим с остатком k на n: k = nt + r, 0 ≤ r
- 8. Примеры. В качестве порождающего элемента можно выбрать число 1 или число –1. Других порождающих элементов у
- 9. Доказательство. (2) следует из (1) и из утверждения (2) теоремы 3.1. Пример. Z6 ={0, 1, 2,
- 10. Теорема 3.4. (о подгруппах циклической группы) (1) Любая подгруппа циклической группы сама является циклической. (2) Имеется
- 11. Таким образом, имеем инъекцию из множества делителей порядка группы G в множество её циклических подгрупп. Следовательно,
- 13. Скачать презентацию










 Историческая задача
Историческая задача Касательная плоскость к сфере
Касательная плоскость к сфере Распределительное свойство
Распределительное свойство Методы решения тригонометрических уравнений
Методы решения тригонометрических уравнений Целые и дробные числа
Целые и дробные числа Решение систем линейных уравнений разными методами
Решение систем линейных уравнений разными методами Параллельные прямые в пространстве
Параллельные прямые в пространстве Второй и третий признаки подобия треугольников
Второй и третий признаки подобия треугольников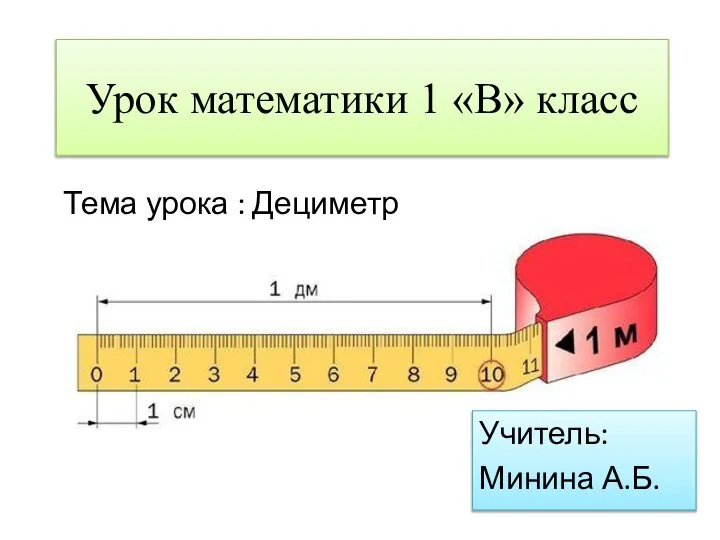 Дециметр
Дециметр Параллельные алгоритмы вычислительной алгебры. Распараллеливание на компьютерах с распределенной памятью
Параллельные алгоритмы вычислительной алгебры. Распараллеливание на компьютерах с распределенной памятью Сложение чисел
Сложение чисел Число и цифра 7. Написание цифр 7. Сравнение чисел в пределах 7
Число и цифра 7. Написание цифр 7. Сравнение чисел в пределах 7 Свидетели истории народа
Свидетели истории народа Тригонометрические уравнения
Тригонометрические уравнения Определение степени с целым отрицательным показателем
Определение степени с целым отрицательным показателем Объём цилиндра. Тест. Решение задач по готовым чертежам
Объём цилиндра. Тест. Решение задач по готовым чертежам Курс по математике ОГЭ 2020
Курс по математике ОГЭ 2020 Комплексные числа. Понятие мнимой единицы
Комплексные числа. Понятие мнимой единицы Площадь фигур - какие они
Площадь фигур - какие они Дисперсия случайной величины и ее свойства
Дисперсия случайной величины и ее свойства Алгебраическая дробь и её основное свойство. 7 класс
Алгебраическая дробь и её основное свойство. 7 класс Экономическая статистика. Демография предприятий
Экономическая статистика. Демография предприятий Решение уравнений с переменной под знаком модуля
Решение уравнений с переменной под знаком модуля Треугольники. Решение задач
Треугольники. Решение задач Презентация на тему Сложение отрицательных и положительных чисел
Презентация на тему Сложение отрицательных и положительных чисел  Булева алгебра. Семинар №2
Булева алгебра. Семинар №2 Задачи на обобщение изученного материала
Задачи на обобщение изученного материала Использование современных программных комплексов в расчете строительных конструкций. Граничные условия в напряжениях
Использование современных программных комплексов в расчете строительных конструкций. Граничные условия в напряжениях