Свойства касательных к окружности. 7 класс

Цели урока:
уметь строить касательную к окружности;
знать понятия касательной, точки касания, отрезков касательных, проведённых из одной точки;
понимать свойство касательной и её признак и показать их применение при решении задач;

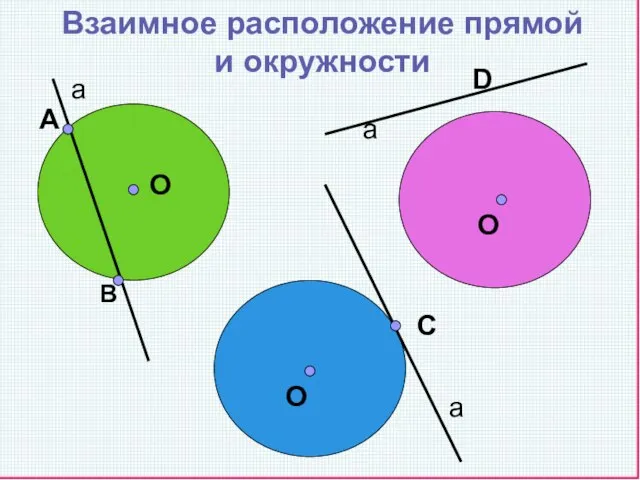
Взаимное расположение прямой
и окружности
А
В
С
О
О
О
D
а
а
а

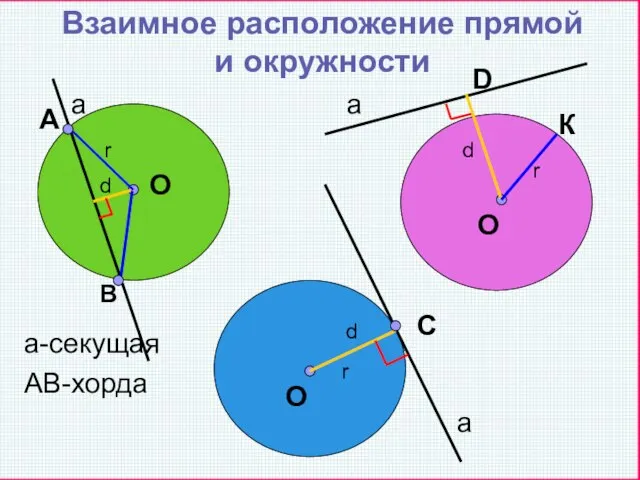
Взаимное расположение прямой
и окружности
А
В
r
d
d
r
d
r
С
О
О
О
К
D
а а
а-секущая
АВ-хорда
а

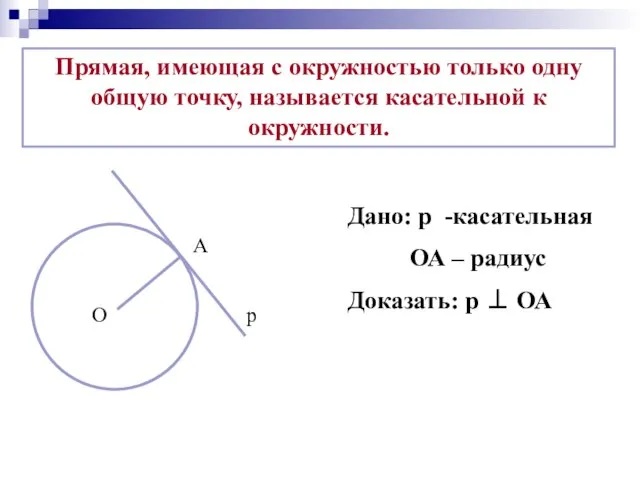
Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности.
А
О
р
Дано: р -касательная
ОА – радиус
Доказать: р ⊥ ОА

Теорема 1
Если расстояние от центра окружности до прямой равно радиусу окружности, то эта прямая является касательной к окружности.
Доказательство. Пусть расстояние от центра О окружности до прямой а равно радиусу R окружности. Опустим из центра О перпендикуляр ОА на эту прямую. Тогда ОА = R. Для любой другой точки B на прямой а наклонная ОB будет больше перпендикуляра ОА и, следовательно, больше R. Таким образом, расстояние от любой точки прямой а, отличной от А, до центра О больше R. Значит, прямая а и окружность имеют одну общую точку А, т.е. прямая касается окружности.

Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
Теорема 2
Докажите самостоятельно.

Теорема 3
Отрезки касательных, проведенных к окружности из одной точки, равны.
Доказательство. Рассмотрим две касательные к окружности с центром в точке О, проведенные из точки А и касающиеся окружности в точках В и С. Треугольники АОВ и АОС прямоугольные, ОВ=ОС и сторона АО общая. По признаку равенства прямоугольных треугольников (по катету и гипотенузе), они равны. Следовательно, АВ=АС.

Вопрос 1
Какая прямая называется касательной к окружности?
Ответ: Касательной к окружности называется прямая, имеющая с окружностью только одну общую точку.

Вопрос 2
В каком случае прямая касается окружности?
Ответ: Если расстояние от центра окружности до прямой равно радиусу окружности.

Вопрос 3
Какой угол образуют касательная к окружности и радиус, проведенный в точку касания?
Ответ: 90о.

Вопрос 4
Что можно сказать об отрезках касательных к окружности, проведенных из одной точки?
Ответ: Они равны.