Содержание
- 2. Обнинский Институт Атомной Энергетики МОДЕЛИРОВАНИЕ ИНФОРМАЦИОННЫХ СИСТЕМ Гулина Ольга Михайловна [email protected] Сopyright © 2001 by Nataly
- 3. Вычисление интегралов методом Монте-Карло
- 4. Метод Монте-Карло Z=g(ξ),
- 5. Общий метод оценки математических ожиданий
- 6. Оценка эмпирической дисперсии
- 7. Общий метод оценки математических ожиданий
- 8. Вычисление интегралов методом Монте-Карло
- 9. Алгоритм вычисления интеграла
- 10. Простейший метод Монте-Карло I= p1(P)=1/SG при P∈G f1(P)=SG*f(P)
- 11. Трудоемкость алгоритма Монте-Карло t*Dξ
- 12. Способы уменьшения дисперсии
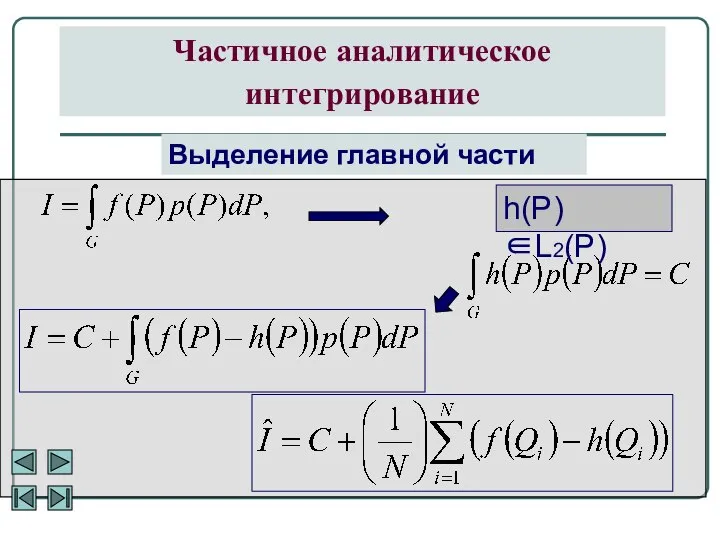
- 13. Частичное аналитическое интегрирование Выделение главной части h(P)∈L2(P)
- 14. Частичное аналитическое интегрирование Выделение главной части если , то и DZ
- 15. Частичное аналитическое интегрирование Интегрирование по части области где 0 G1=G\B
- 16. Частичное аналитическое интегрирование Интегрирование по части области В G1 p1(P)=p(P)/(1-c) DZ`
- 17. 2 Метод существенной выборки Плотность p(P), определенную в G, назовем допустимой по отношению к f(P), если
- 18. Метод существенной выборки
- 19. Теорема. Минимальная дисперсия DZ0 реализуется в случае, когда плотность p(P) пропорциональна |f(P)|, и равна Метод существенной
- 20. Метод существенной выборки Метод предложен Г. Каном и называется методом существенной выборки (importance sampling)
- 22. Скачать презентацию


















 Анализ представленности геометрического материала в учебнике М.И. Моро (1-4 класс)
Анализ представленности геометрического материала в учебнике М.И. Моро (1-4 класс) Симметрия в пространстве
Симметрия в пространстве Приобретать знания- храбрость, приумножать их – мудрость, а умело приумножать- великое искусство.
Приобретать знания- храбрость, приумножать их – мудрость, а умело приумножать- великое искусство. Тригонометрия. Комплексные числа
Тригонометрия. Комплексные числа Область определения функции. С/Р
Область определения функции. С/Р Презентация на тему Квадрат
Презентация на тему Квадрат  повторение 8 класса
повторение 8 класса Анализ контрольной работы
Анализ контрольной работы Обучение для выполнения НИР 5 курса. Занятие №2
Обучение для выполнения НИР 5 курса. Занятие №2 Презентация на тему Метод параллельного проектирования
Презентация на тему Метод параллельного проектирования  Тригонометрические функции числового аргумента
Тригонометрические функции числового аргумента Вычитание в пределах 20 с переходом через разряд. Тренажер
Вычитание в пределах 20 с переходом через разряд. Тренажер Пифагор Самосский
Пифагор Самосский Прикладная математика. Лекция 10. Контрольная работа
Прикладная математика. Лекция 10. Контрольная работа Презентация на тему: Турнир смекалистых
Презентация на тему: Турнир смекалистых Вычитание смешанных чисел
Вычитание смешанных чисел Предел числовой последовательности
Предел числовой последовательности Задача предельного типа. Мир арифметики
Задача предельного типа. Мир арифметики Вычитание смешанных чисел
Вычитание смешанных чисел Тест № 2 по теме Функция
Тест № 2 по теме Функция Упрощение выражений. Восстановите цепочку вычислений
Упрощение выражений. Восстановите цепочку вычислений Системы принятия решений. Алгоритмы оптимизации
Системы принятия решений. Алгоритмы оптимизации Презентация на тему Сравнение трехзначных чисел (3 класс)
Презентация на тему Сравнение трехзначных чисел (3 класс)  Логика высказываний. Таблица истинности логических союзов
Логика высказываний. Таблица истинности логических союзов Действия с дробями
Действия с дробями Понятие функции. Свойства функций
Понятие функции. Свойства функций Составление краткой записи и решение задач
Составление краткой записи и решение задач Презентация на тему Тренажер по математике 2 класс
Презентация на тему Тренажер по математике 2 класс