переселить из номера n в номер n+1, а нового в номер 1, если приехало двое то всех из n в n+2, а новых в первый и во второй.
Если к отелю подъезжает бесконечный автобус полный новыми постояльцами, то за n берется номер постояльца, а так же номер пассажира автобуса и всех постояльцев нужно переселить в номер 2n, а новых в n.
Если к отелю подъезжает бесконечное количество бесконечных автобусов полных новыми постояльцами, тогда есть 4варианта действий, рассмотрен будет только метод факторизации простых чисел. Всех постояльцев нужно пасадить в отдельный автобус и поставить в очередь, после чего номер места в автобусе обозначить за n, а номер автобуса за c, после чего начать заселять всех в номера 2^n×3^c. Данный метод оставляет много номеров незанятыми, но работает с более высшими уровнями степеней.








 Угол между векторами
Угол между векторами Танграм: от истории к современности
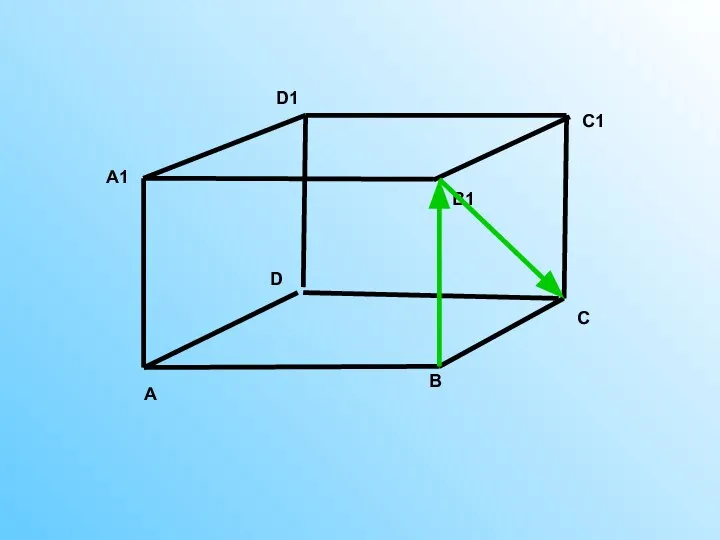
Танграм: от истории к современности Тетраэдр параллелепипед. 10 класс
Тетраэдр параллелепипед. 10 класс Розвязування задач
Розвязування задач Методы многокритериальной оптимизации
Методы многокритериальной оптимизации Векторная алгебра. Скалярное, векторное и смешанное произведения векторов. Лекция 2
Векторная алгебра. Скалярное, векторное и смешанное произведения векторов. Лекция 2 Построение сечения
Построение сечения Среднее арифметическое
Среднее арифметическое Презентация на тему Признаки параллельности прямых
Презентация на тему Признаки параллельности прямых  Нумерация. Сложение и вычитание. Геометрические фигуры и величины
Нумерация. Сложение и вычитание. Геометрические фигуры и величины Классификация треугольников
Классификация треугольников Практические задания на применение формул сокращённого умножения
Практические задания на применение формул сокращённого умножения Численные методы решения систем линейных уравнений
Численные методы решения систем линейных уравнений Периметр многоугольника (2 класс)
Периметр многоугольника (2 класс) Pakāpes vingrinājumi (bez atb)
Pakāpes vingrinājumi (bez atb) Куб
Куб Симметрия вокруг нас
Симметрия вокруг нас Интегративные процессы математического образования и профессиональная подготовка учащихся
Интегративные процессы математического образования и профессиональная подготовка учащихся Подготовка к контрольной работе
Подготовка к контрольной работе Презентация на тему Знаки больше, меньше, равно (1 класс)
Презентация на тему Знаки больше, меньше, равно (1 класс)  Сфера. Окружность и круг
Сфера. Окружность и круг Решение задач
Решение задач Станция Решай-ка. Математический экспресс
Станция Решай-ка. Математический экспресс Как построить графики функций y = f(x) + b и y = f(x + a), если известен график функции y = f(x)
Как построить графики функций y = f(x) + b и y = f(x + a), если известен график функции y = f(x) 2.МатСтатистика-Критерии и Различия
2.МатСтатистика-Критерии и Различия Теория функций комплексных переменных
Теория функций комплексных переменных Способы быстрого счета
Способы быстрого счета Презентация на тему Сумма и разность десятичных дробей
Презентация на тему Сумма и разность десятичных дробей