Содержание
- 2. Основные числовые системы Система натуральных чисел Кольцо целых чисел Поле рациональных чисел Система действительных чисел Поле
- 3. Аналитические преобразования с помощью компьютера Особенности аналитических вычислений на компьютерах : имеется возможность проводить аналитические (и
- 4. Основная цель компьютерной алгебры – изучение алгоритмов аналитических преобразований точки зрения их эффективной реализации на компьютере.
- 5. Эффективность алгоритмов Качество (эффективность) алгоритма обычно оценивают асимптотической сложностью, то есть порядком роста сложности как функции
- 6. Характеристики алгоритмов
- 7. Характеристики алгоритмов после ускорения.
- 8. В зависимости от порядка сложности и вида результирующих данных алгоритмы компьютерной математики можно отнести к четырем
- 9. Алгебра Алгеброй называется упорядоченная пара , где А - непустое множество, V - множество операций на
- 10. Моноид Алгебра типа (2, 0), где A - произвольная непустое множество; * - ассоциативная бинарная операция
- 11. Таким образом, группа – это непустое множество с двумя операциями на нем, бинарной операцией * и
- 12. Кольцо Кольцом называется алгебра K =〈K,+,-,·,1 〉 типа (2,1,2,0) , главные операции которой удовлетворяют следующим условиям:
- 13. Поле Полем называется коммутативное кольцо, в котором нуль отличен от единицы, , и всякий ненулевой элемент
- 14. I. II. III. IV. V. VI. Если и а) б) тогда А=N Система натуральных чисел Системой
- 15. Кольцо целых чисел Кольцо K называется кольцом целых чисел, если аддитивное группа кольца K является аддитивной
- 16. Поле рациональных чисел Полем рациональных чисел называется поле частных кольца целых чисел. Элементы поля рациональных чисел
- 17. Система действительных чисел Системой действительных чисел называется полное архимедовски упорядоченное поле. назад
- 19. Скачать презентацию




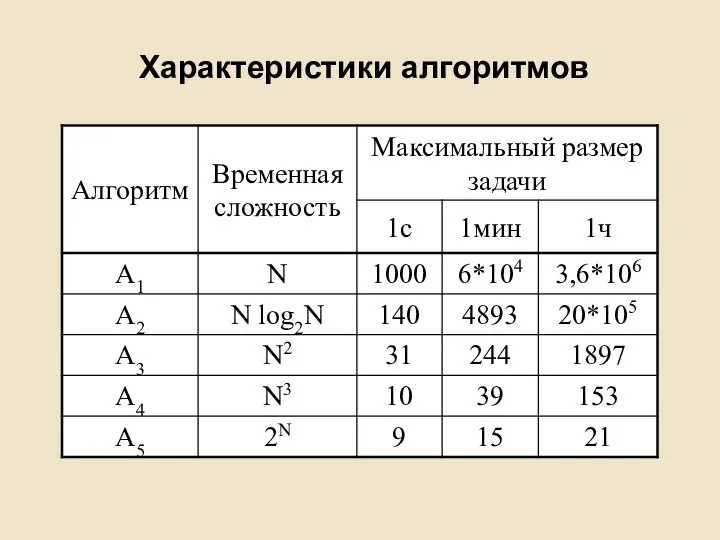
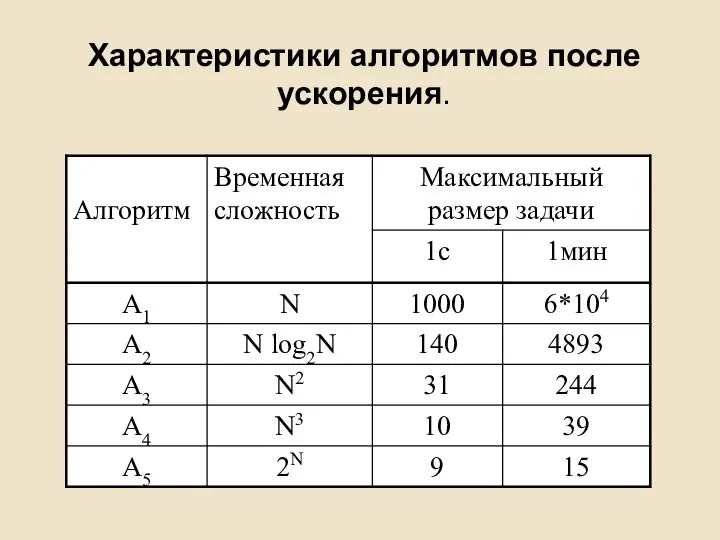










 График равномерного движения
График равномерного движения Тренажёр. Табличное умножение
Тренажёр. Табличное умножение Основные теоремы о дифференцируемых функциях
Основные теоремы о дифференцируемых функциях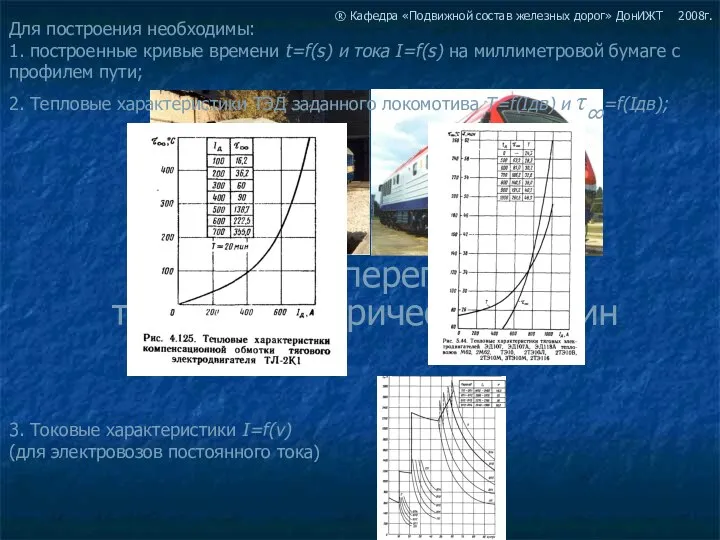 Расчет перегрева тяговых электрических машин
Расчет перегрева тяговых электрических машин Составление словосочетаний, предложений с местоимениями. Морфологический разбор местоимения
Составление словосочетаний, предложений с местоимениями. Морфологический разбор местоимения Задачи на части
Задачи на части Графики функций
Графики функций Презентация на тему Прогрессии
Презентация на тему Прогрессии  Решение простейших тригонометрических уравнений
Решение простейших тригонометрических уравнений Финансовая математика: банки, вклады, кредиты. Часть 2
Финансовая математика: банки, вклады, кредиты. Часть 2 Система единиц физических величин
Система единиц физических величин Тригонометрические функции числового аргумента
Тригонометрические функции числового аргумента Материал для внеклассной работы по математике. Бедный заяц (сказка)
Материал для внеклассной работы по математике. Бедный заяц (сказка) Проверочный тест 1 по геометрии
Проверочный тест 1 по геометрии Деление десятичной дроби на 10,100,1000
Деление десятичной дроби на 10,100,1000 Вычислите устно. Задания
Вычислите устно. Задания Решение дифференциальных уравнений методом ломаных Эйлера с использованием электронных таблиц MS Excel
Решение дифференциальных уравнений методом ломаных Эйлера с использованием электронных таблиц MS Excel Задачи. Самостоятельная работа
Задачи. Самостоятельная работа Параллелепипед. Объем параллелепипеда
Параллелепипед. Объем параллелепипеда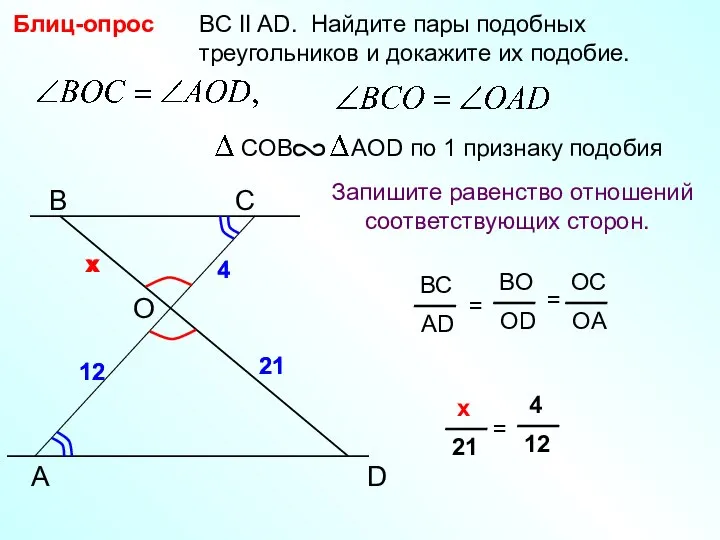 Признаки подобия треугольников
Признаки подобия треугольников Перпендикулярность прямых, прямой и плоскости
Перпендикулярность прямых, прямой и плоскости Практикум по решению комбинированных уравнений
Практикум по решению комбинированных уравнений Признаки параллельности прямых
Признаки параллельности прямых Взаимно обратные числа
Взаимно обратные числа Параллельные прямые
Параллельные прямые Найди соседей. Дидактическая игра
Найди соседей. Дидактическая игра Исследование функции при помощи производной
Исследование функции при помощи производной Квадратное уравнение и его корни. Решение полных квадратных уравнений
Квадратное уравнение и его корни. Решение полных квадратных уравнений