Решение задач

№ 636
О
A
B
C
< ACB = 120
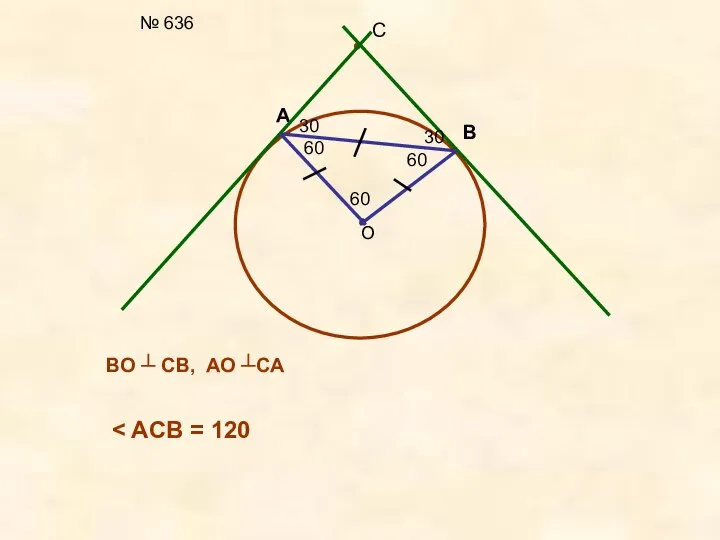
60
60
60
30
30
BO ┴ CB, AO ┴CA

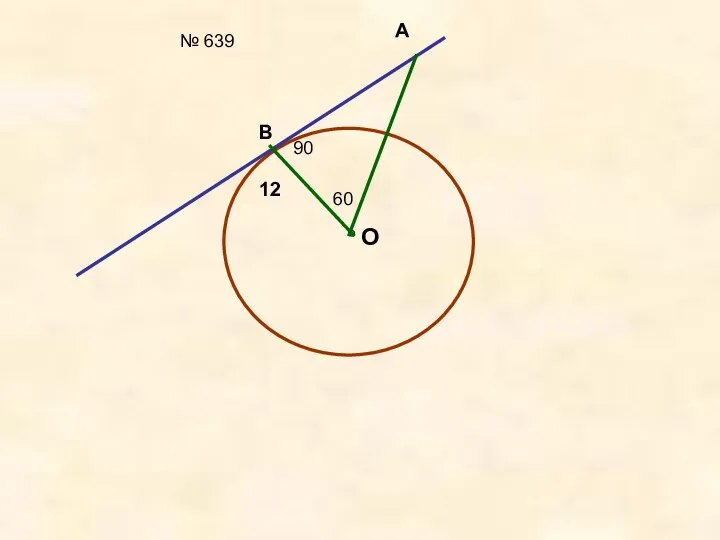
№ 639
O
B
A
60
12
90

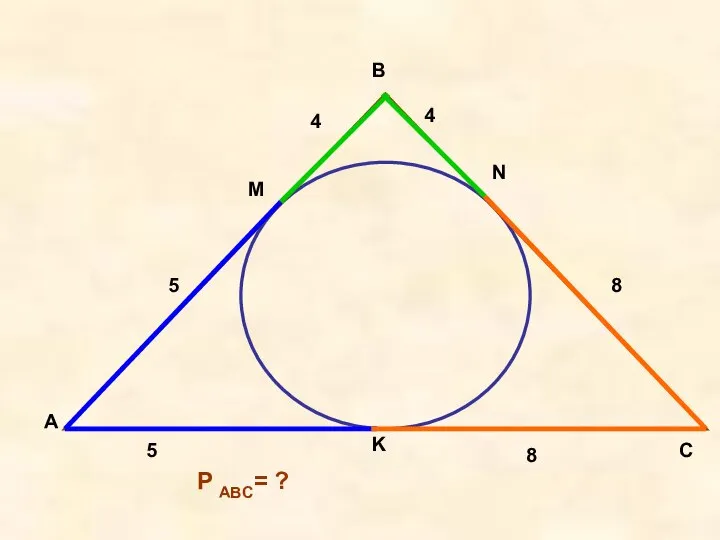
A
B
C
M
N
K
4
5
8
P ABC= ?
4
5
8

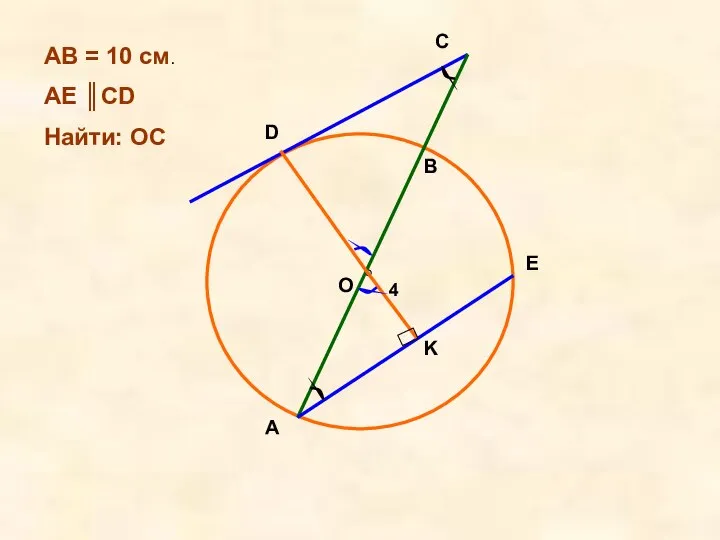
O
D
C
A
B
E
K
4
AB = 10 см.
AE ║CD
Найти: OC

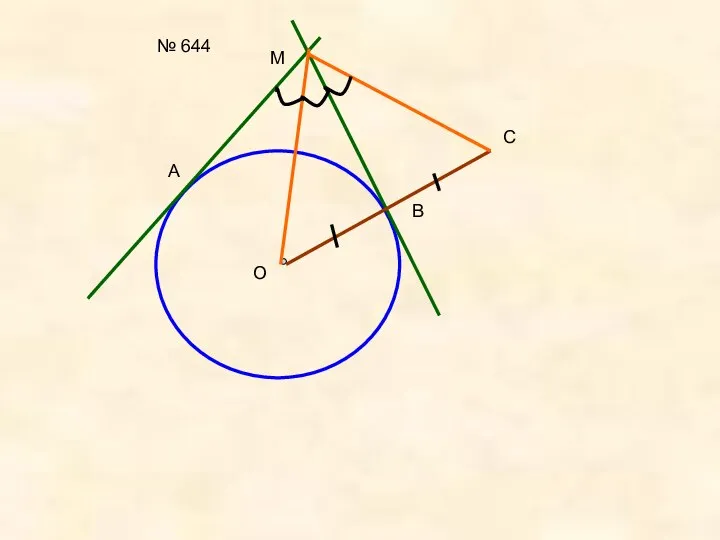
№ 644
O
A
M
B
C

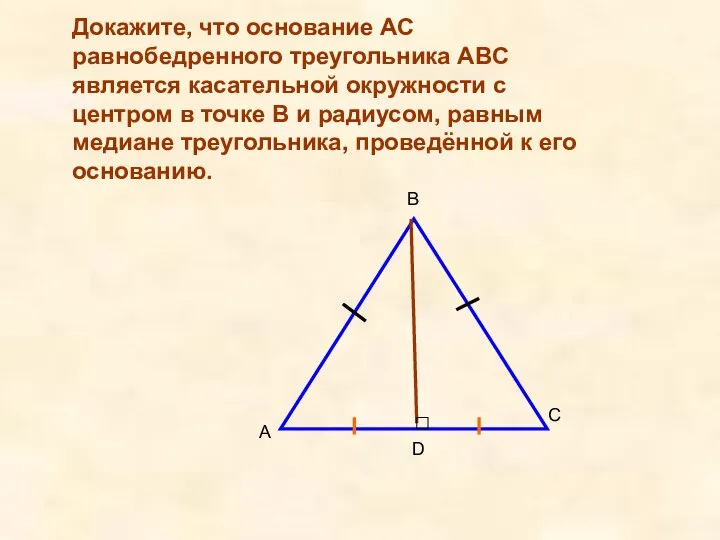
Докажите, что основание AC равнобедренного треугольника ABC является касательной окружности с центром в точке B и радиусом, равным медиане треугольника, проведённой к его основанию.
B
A
C
D

Домашнее задание
П. 69, № 643, № 645