Асимптоты. Вертикальная асимптота

Содержание
Вертикальная асимптота
Горизонтальная асимптота
Наклонная асимптота
Связь между наклонной и горизонтальной асимптотами
Порядок нахождения асимптот
Нахождение вертикальных асимптот
Нахождение горизонтальных асимптот
Нахождение двух пределов
Нахождение наклонных асимптот
Выделение целой части у наклонных асимптот
Использованные сайты

Вертикальная асимптота
Это прямая вида x = a при условии существования
предела .
Как правило, при определении вертикальной
асимптоты ищут не один предел, а два односторонних
(левый и правый). Это делается с целью определить,
как функция ведёт себя по мере приближения к
вертикальной асимптоте с разных сторон. Например:
1.)
2.)
Замечание: обратите внимание на знаки
бесконечностей в этих равенствах.

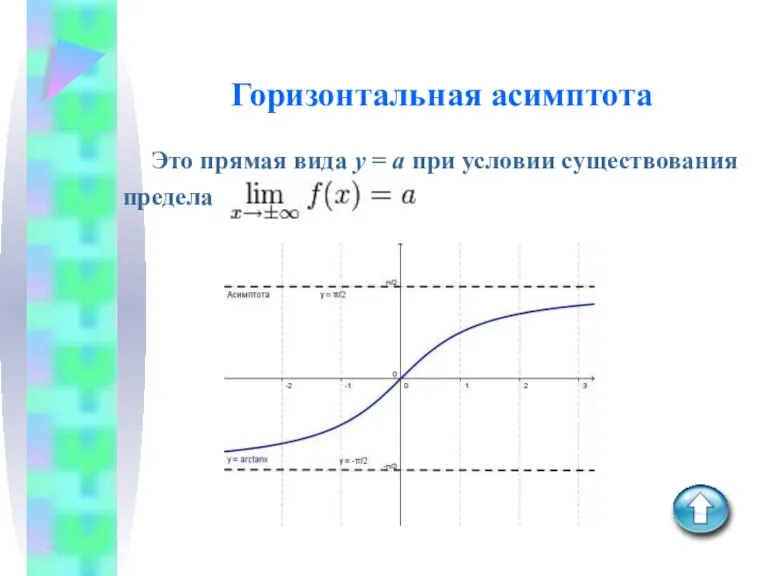
Горизонтальная асимптота
Это прямая вида y = a при условии существования
предела .

Наклонная асимптота
Это прямая вида y = kx + b при условии
существования пределов:
1.)
2.)
Замечание: функция может иметь не более двух
наклонных (горизонтальных) асимптот!
Замечание: Если хотя бы один из двух упомянутых
выше пределов не существует (т.е. равен ∞), то
наклонной асимптоты при x → + ∞ (или x → - ∞) не
существует!

Связь между наклонной и горизонтальной асимптотами
В случае, если наклонная асимптота расположена
горизонтально, то есть при k = 0, она называется
горизонтальной асимптотой. Таким образом,
горизонтальная асимптота является частным случаем
наклонной асимптоты при .

Из выше указанных замечаний следует, что
функция имеет или только одну наклонную
асимптоту, или одну горизонтальную асимптоту, или
одну наклонную и одну горизонтальную, или две
наклонных, или две горизонтальных, либо же вовсе не
имеет асимптот;
существование указанных в первом пункте асимптот
напрямую связано с существованием соответствующих
пределов.

Порядок нахождения асимптот
Нахождение вертикальных асимптот;
Нахождение горизонтальных асимптот;
Нахождение двух пределов ;
Нахождение двух пределов .

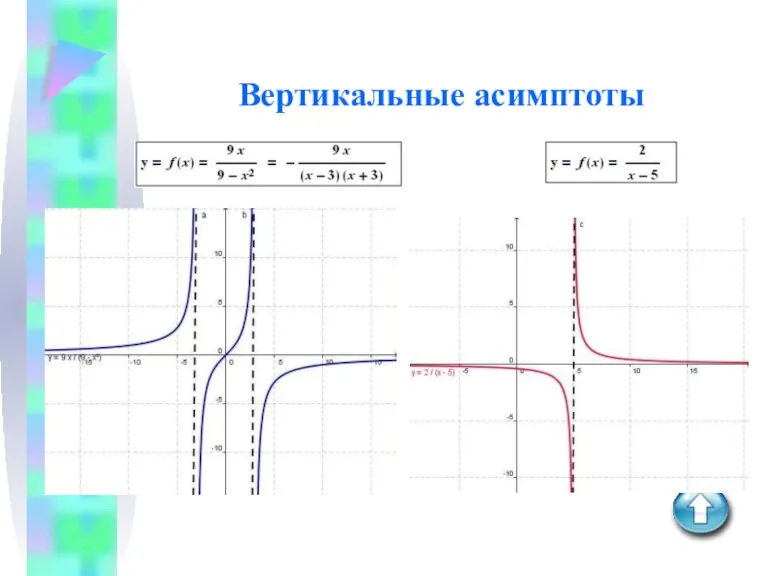
Нахождение вертикальных асимптот
Из определения асимптоты следует, что прямая х = а –
асимптота кривой y = f(x).
Например, для функции f(x) = 2/(x – 5) прямая х = 5
является вертикальной асимптотой.
У функции прямые х = 3 и х = -3
являются вертикальными асимптотами кривой.
Вертикальных асимптот график не имеет, если область
определения не имеет граничных точек. (У графиков
многочленов не бывает вертикальных асимптот.)
Например, f(x) = 2x³ - 3x² + x + 5 не имеет
вертикальных асимптот.

Вертикальные асимптоты

Нахождение горизонтальных асимптот
Следовательно, горизонтальная прямая y = 1 служит
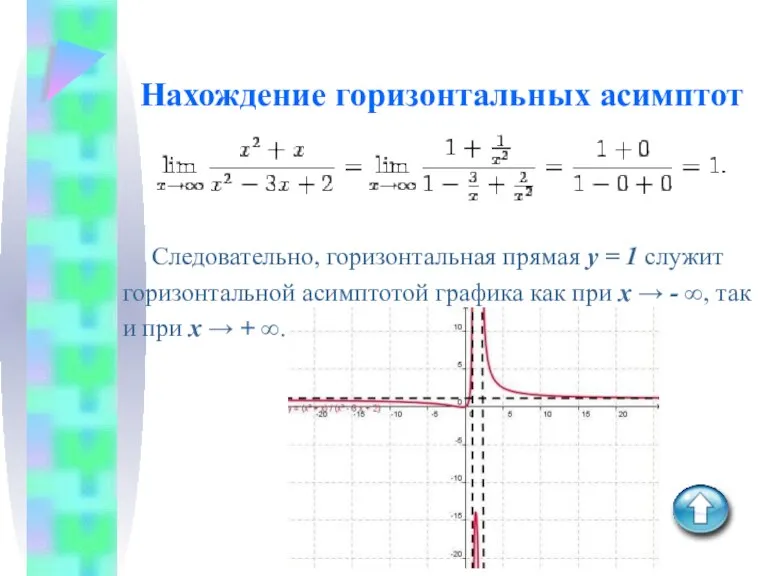
горизонтальной асимптотой графика как при x → - ∞, так
и при x → + ∞.

Нахождение двух пределов
Если k = 0 в предыдущем пункте нахождения двух
пределов, то kx = 0, и предел
ищется по формуле горизонтальной асимптоты,
.

Нахождение наклонных асимптот
Находятся по формуле:
где
.
Также наклонную асимптоту можно найти, выделив
целую часть.

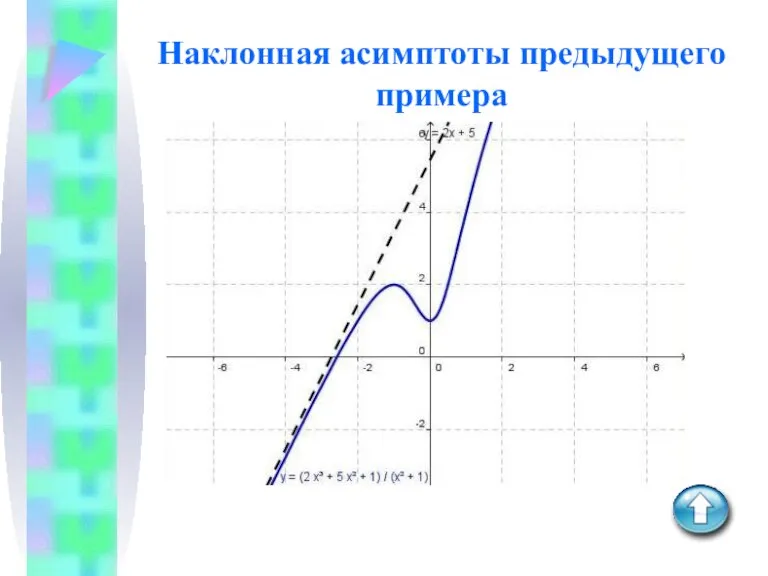
Выделение целой части у наклонных асимптот
Например, дана функция
Разделив нацело числитель на знаменатель, получим:
При x → ∞, , то есть:
, и
y = 2x + 5 является искомым уравнением асимптоты.

Наклонная асимптоты предыдущего примера