Корни натуральной степени из числа и их свойства

Корнем n – й степени из действительного числа a (n – натуральное число) называют такое действительное число x, при возведении которого в степень n получается число a.
Это число обозначают: x=
a - подкоренное выражение
n - показатель корня
Неотрицательное значение корня n –й степени из неотрицательного числа называется арифметическим корнем.

Операция извлечения корня является обратной
по отношению к возведению в соответствующую
степень.
5² = 25
10³ = 1000
0,3⁴ = 0,0081

Пример 1:
Вычислить: а) √ 49; б) √ 0,125; в) √ 0 ; г) √ 17
3
7
4

Корень чётной степени имеет смысл (т.е. определён) только для неотрицательного подкоренного выражения; корень нечётной степени имеет смысл для любого подкоренного выражения.
Корнем нечётной степени n из отрицательного числа a (n=3,5,…) называют такое отрицательное число, которое при возведении в степень n даёт в результате число a.
Подобные корни

1.Корень n-степени (n=2,3,4,5, …) из произведения неотрицательных чисел равен произведению корней n-степени из этих чисел:
=
Пример:
=
=
2*3=6
Свойства корней n-степени

2. Чтобы извлечь корень из дроби, нужно извлечь корень из числителя и знаменателя отдельно и первый результат разделить на второй:
=
Пример:
=
=

3. Если a≥0, n=2,3,4,5,… и k – любое натуральное число, то справедливо равенство:
Пример:

4. Если a≥0, n и k - натуральные числа, большие 1, то справедливо равенство:
Пример:

5. Если показатели корня и подкоренного выражения умножить или разделить на одно и то же отличное от нуля число, то значение корня не изменится:
Пример:

6. Чтобы извлечь корень из степени, показатель которой делится на показатель корня, нужно показатель степени разделить на показатель корня:
Пример:

Приближенные значения корней умели находить еще жители древнего Вавилона около 4 тысяч лет назад. Не имея вычислительных машин, люди применяли формулу, автор которой неизвестен:

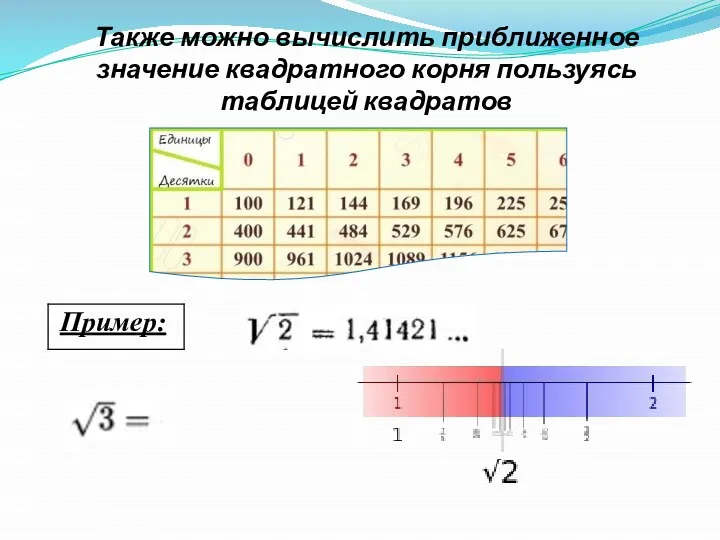
Также можно вычислить приближенное значение квадратного корня пользуясь таблицей квадратов