Иррациональные неравенства

Уравнение называется иррациональным если неизвестное находится под знаком корня. Решение любого иррационального уравнения состоит из трех частей:
1) Найти ОДЗ.
2) Решить уравнение соответствующим способом. Чаще всего возведением обеих частей иррационального уравнения в квадрат.
3) Сделать письменно проверку и записать ответ.

ЗАКОН ЗАПИСИ ОДЗ:
1) знаменатель дроби не равен нулю
2) то, что стоит внутри квадратного корня или корня четной степени ≥ 0
Примечание.
Кубические корни и корни нечетной степени в ОДЗ не нуждаются.

Решение иррациональных неравенств вида:
.

Решение иррациональных неравенств вида:
.

Решение иррациональных неравенств вида:
.

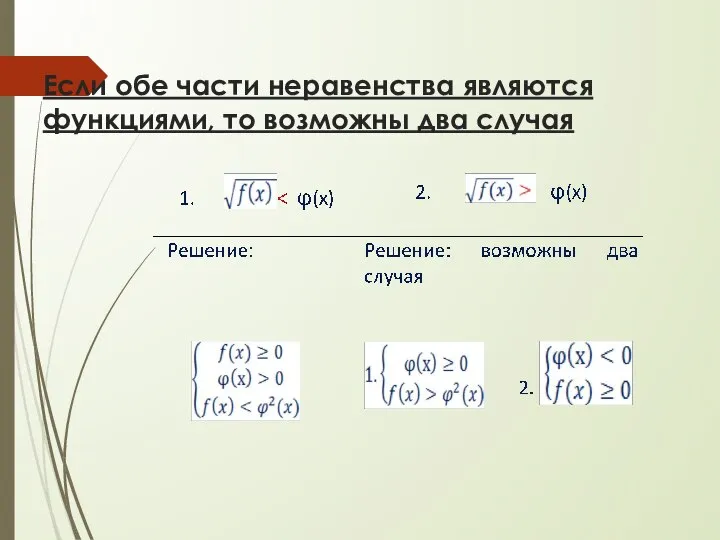
Если обе части неравенства являются функциями, то возможны два случая