Содержание
- 2. 1. Вычислите: 2
- 3. Вычислите: Коэффициенты при a и b запишем в виде треугольника.
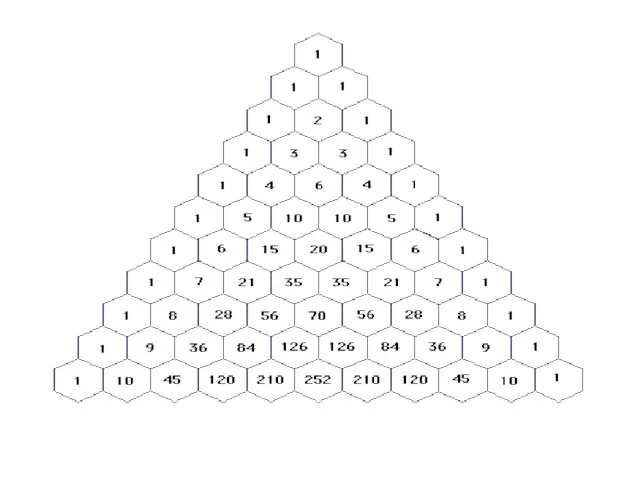
- 4. Треугольник Паскаля – Это бесконечная числовая таблица «треугольной формы», в которой по боковым сторонам стоят единицы
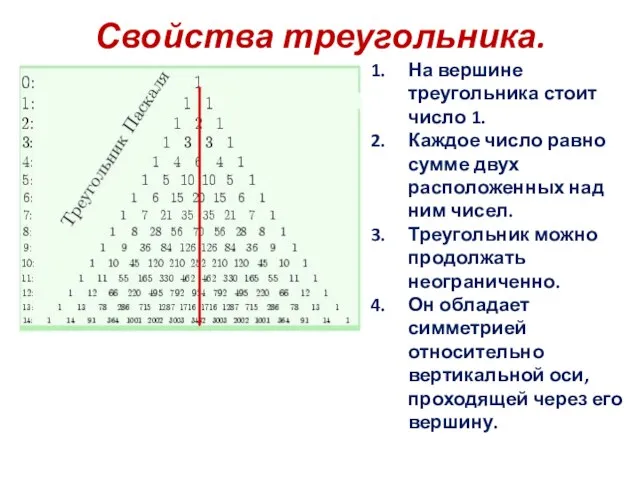
- 7. Свойства треугольника. На вершине треугольника стоит число 1. Каждое число равно сумме двух расположенных над ним
- 8. Свойства треугольника. 5. Чтобы найти сумму чисел, стоящих на любой диагонали от начала до интересующего нас
- 9. Где применяется треугольник Паскаля? Правила: - чтобы возвести сумму или разность одночленов в любую степень смотрим
- 10. Правила: - чтобы возвести сумму или разность одночленов в любую степень смотрим соответствующую степени строчку в
- 11. Задача 1: В урне находится 7 шаров: 2 белых, 4 черных и 1 красный. Вынимается один
- 12. Задача 2: Вычислить вероятность выпадения в сумме 10 очков при бросании пары костей. Выпадение в сумме
- 13. Задача 3: В коробке лежат 8 зеленых, 7 синих и 15 красных карандашей. Вычислить вероятность того,
- 14. Задача 4: В одной коробке находится 4 белых и 8 черных шаров, а в другой –
- 15. Задача 5: В аквариуме плавает 100 рыбок. Известно, что из них 17 золотых, 4 исполняют желания.
- 17. Скачать презентацию












 Преемственность в формировании УПК младших школьников и учащихся 5-6 классов на уроках математики посредством интеграции
Преемственность в формировании УПК младших школьников и учащихся 5-6 классов на уроках математики посредством интеграции Геометрия Евклида
Геометрия Евклида Почему нельзя делить на ноль
Почему нельзя делить на ноль Определение синуса, косинуса, тангенса острого угла прямоугольного треугольника
Определение синуса, косинуса, тангенса острого угла прямоугольного треугольника Точка, отрезок, луч, прямая
Точка, отрезок, луч, прямая Интерактивная дидактическая игра Состав чисел до 10. Математика, 1 класс
Интерактивная дидактическая игра Состав чисел до 10. Математика, 1 класс Презентация на тему Дробные выражения (6 класс)
Презентация на тему Дробные выражения (6 класс)  Правило Лопиталя. Семинар 17
Правило Лопиталя. Семинар 17 Презентация на тему Построение графиков функций, содержащих выражения под знаком модуля
Презентация на тему Построение графиков функций, содержащих выражения под знаком модуля 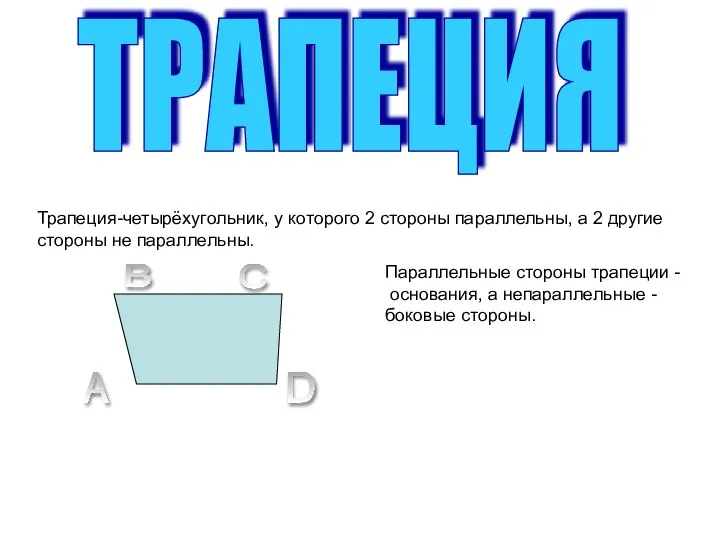 Трапеция
Трапеция Урок математики в 10 классе по теме Пирамида
Урок математики в 10 классе по теме Пирамида Общее уравнение прямой и плоскости. Лекция1 (1)
Общее уравнение прямой и плоскости. Лекция1 (1) Умножение и деление десятичных дробей на натуральное число
Умножение и деление десятичных дробей на натуральное число Презентация на тему Понятие одночлена стандартный вид одночлена (7 класс)
Презентация на тему Понятие одночлена стандартный вид одночлена (7 класс)  Второй признак равенства треугольников. Урок 16
Второй признак равенства треугольников. Урок 16 Соотношения между сторонами и углами прямоугольного треугольника. Синус, косинус, тангенс и котангенс острого угла
Соотношения между сторонами и углами прямоугольного треугольника. Синус, косинус, тангенс и котангенс острого угла Решение примеров и уравнений
Решение примеров и уравнений L_3_U
L_3_U Презентация по математике "Число 5. Цифра 5" -
Презентация по математике "Число 5. Цифра 5" -  Цилиндр
Цилиндр Fraktaly_Osnovnye_ponyatia (1)
Fraktaly_Osnovnye_ponyatia (1) Действительные числа
Действительные числа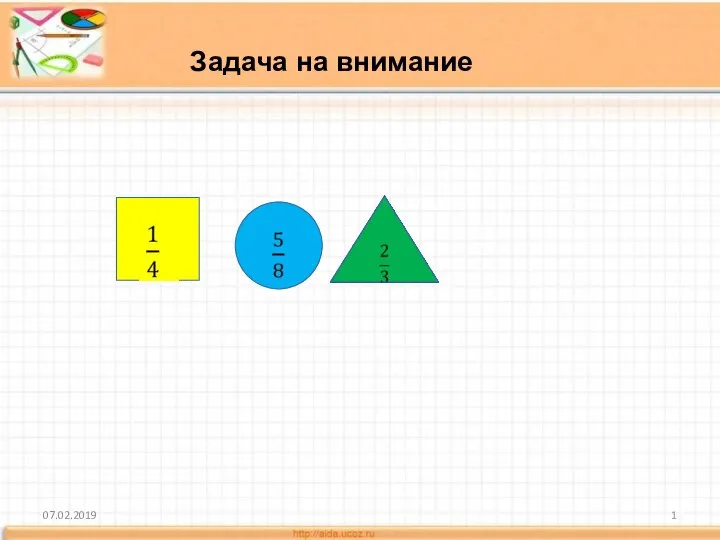 Задача на внимание. 5 класс
Задача на внимание. 5 класс Булеві функції. Перетворення логічних виразів. КНФ та ДНФ. СКНФ та СДНФ. Контрольна робота
Булеві функції. Перетворення логічних виразів. КНФ та ДНФ. СКНФ та СДНФ. Контрольна робота Площадь параллелограмма
Площадь параллелограмма Умножение двузначных чисел
Умножение двузначных чисел Число 5
Число 5 Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей