Слайд 2Уравнение есть равенство,
которое еще не является истинным,
но которое стремятся сделать

истинным,
не будучи уверенным, что этого можно достичь.
А. Фуше
Слайд 3 Прежде всего, уточним, тригонометрическое уравнение - это уравнение, содержащее неизвестное в

тригонометрической функции, и для нахождения его корней необходимо с помощью различных преобразований свести данное уравнение к простейшему тригонометрическому уравнению, а затем найти неизвестное.
Слайд 4 Существуют общие методы решений уравнений как тригонометрических, так и показательных и

логарифмических.
Мы знаем такие методы как:
сведение к квадратным уравнениям;
разложение на множители;
введение новой переменной (вспомогательного угла);
однородные уравнения;
различные преобразования с помощью формул;
использование ограниченности функций;
функционально-графический метод;
и др.
Слайд 5функционально-графический метод решения уравнений
основан на применении свойств тригонометрических функций

и анализа построения графиков функций.
Этот метод является общим для различных уравнений, поэтому знание его поможет в решении многих уравнений
Слайд 6Примерами, в решении которых используется данный метод, могут быть

Слайд 11Графически решить это уравнение сложно, но можно воспользоваться свойствами данных функций.

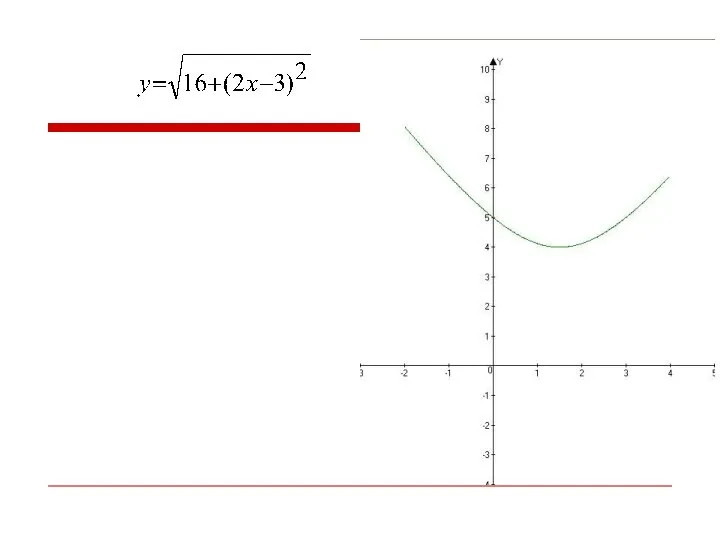
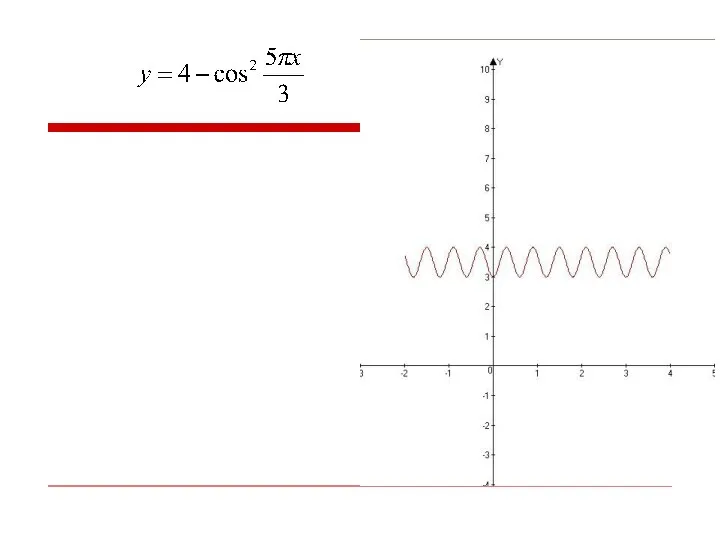
Слайд 15Рассмотрим еще пример
с использованием данного метода

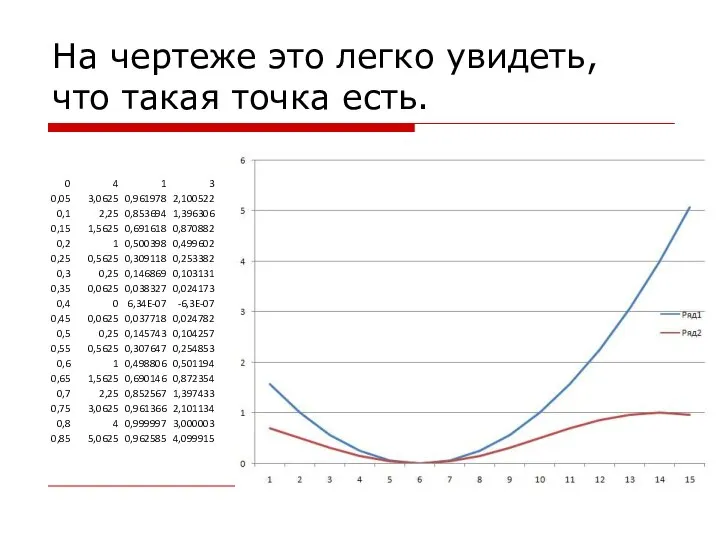
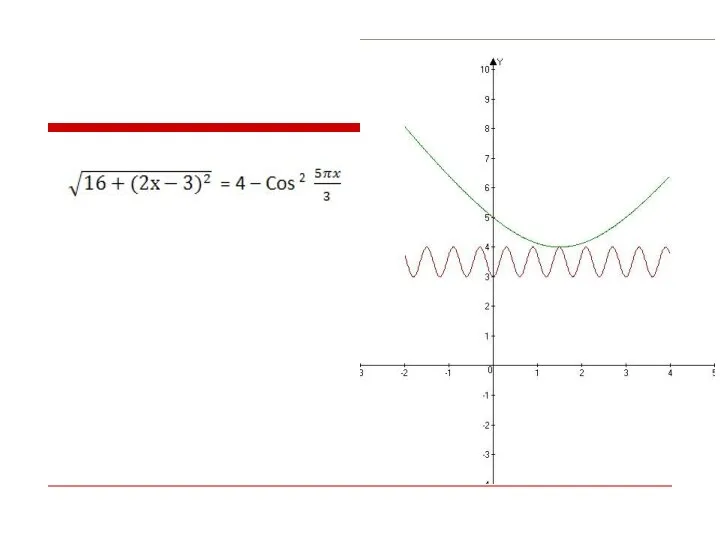
Слайд 16На чертеже это легко увидеть, что такая точка есть.













 Формулы сложения
Формулы сложения Углы, связанные с окружностью
Углы, связанные с окружностью Стереометрия. Основные фигуры в пространстве
Стереометрия. Основные фигуры в пространстве Математика. Лекция 2. Ранг матрицы. Системы линейных уравнений
Математика. Лекция 2. Ранг матрицы. Системы линейных уравнений Арифметическая прогрессия. 9 класс
Арифметическая прогрессия. 9 класс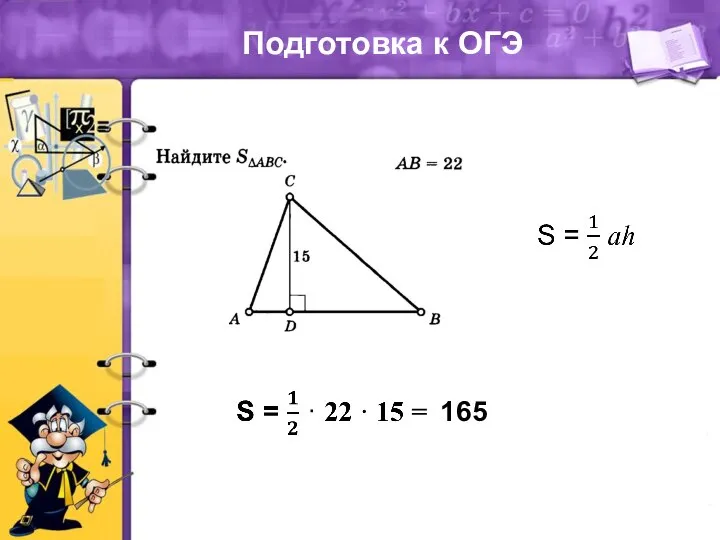 Теорема площади треугольника. Подготовка к ОГЭ
Теорема площади треугольника. Подготовка к ОГЭ Пирамиды. Правильная пирамида
Пирамиды. Правильная пирамида Степень с отрицательным показателем
Степень с отрицательным показателем Математические записи и схемы
Математические записи и схемы Тригонометрия. Комплексные числа
Тригонометрия. Комплексные числа Применение производной к построению графиков функции
Применение производной к построению графиков функции Линейные алгоритмы
Линейные алгоритмы Стереометрия. Базовые понятия. Определения
Стереометрия. Базовые понятия. Определения Презентация на тему Системы линейных уравнений с двумя переменными
Презентация на тему Системы линейных уравнений с двумя переменными  Применение интегральной технологии при изучении алгебраических уравнений
Применение интегральной технологии при изучении алгебраических уравнений Иррациональные неравенства
Иррациональные неравенства Генерация k-элементных подмножеств
Генерация k-элементных подмножеств Урок с применением ИКТ Они были первыми
Урок с применением ИКТ Они были первыми Презентация на тему Площадь многоугольников
Презентация на тему Площадь многоугольников  Математический хоккей
Математический хоккей Математический диктант
Математический диктант Задачи на пропорцию
Задачи на пропорцию Числовые последовательности
Числовые последовательности Угол между векторами
Угол между векторами Малоизвестные, но очень интересные теоремы планиметрии
Малоизвестные, но очень интересные теоремы планиметрии Ознакомление с задачей в 2 действия
Ознакомление с задачей в 2 действия Влияние коэффициентов линейной функции на ее график
Влияние коэффициентов линейной функции на ее график Дроби. Тест
Дроби. Тест