- Главная
- Математика
- Квадратные корни

Содержание
- 2. . КВАДРАТНЫЙ КОРЕНЬ ИЗ ПИРАМИДЫ ХЕОПСА В 2500 ГГ. ДО Н.Э. В ДРЕВНЕМ ЕГИПТЕ ВОЗВОДИЛИСЬ ПИРАМИДЫ
- 3. ПОНЯТИЕ КВАДРАТНЫХ КОРНЕЙ ЧИСЛА ВОЗНИКЛО ОКОЛО 4 ТЫСЯЧ ЛЕТ НАЗАД В ВАВИЛОНЕ. ЕЩЕ В ВАВИЛОНЕ БЫЛИ
- 4. Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а. ОПРЕДЕЛЕНИЕ ЧТО ТАКОЕ
- 5. СВОЙСТВА КОНЕЙ
- 6. СВОЙСТВО КОРНЕЙ
- 7. СВОЙСТВО КОРНЕЙ
- 9. Скачать презентацию
Слайд 2.
КВАДРАТНЫЙ КОРЕНЬ ИЗ ПИРАМИДЫ ХЕОПСА
В 2500 ГГ. ДО Н.Э. В ДРЕВНЕМ
.
КВАДРАТНЫЙ КОРЕНЬ ИЗ ПИРАМИДЫ ХЕОПСА
В 2500 ГГ. ДО Н.Э. В ДРЕВНЕМ

ЕГИПТЕ ВОЗВОДИЛИСЬ ПИРАМИДЫ – УСЫПАЛЬНИЦЫ ФАРАОНОВ.
АРХЕОЛОГИ ПРОСЧИТАЛИ, ЧТО БЕЗ ЗНАНИЯ ЧИСЛА Π И КВАДРАТНОГО КОРНЯ ПОСТРОИТЬ ТАКИЕ СООРУЖЕНИЯ С ЧЕТКО ВЫСТРОЕННЫМИ КОРИДОРАМИ И СТРОГОЙ ОРИЕНТАЦИЕЙ ПОМЕЩЕНИЙ ПО СТОРОНАМ СВЕТА БЫЛО ПРОСТО НЕВОЗМОЖНО.
ГРАФФИТИ НА СТЕНАХ КАМЕННЫХ БЛОКОВ НЕ ДОНЕСЛИ ДО СОВРЕМЕННОСТИ ИМЕН ГЕНИАЛЬНЫХ МАТЕМАТИКОВ.
АРХЕОЛОГИ ПРОСЧИТАЛИ, ЧТО БЕЗ ЗНАНИЯ ЧИСЛА Π И КВАДРАТНОГО КОРНЯ ПОСТРОИТЬ ТАКИЕ СООРУЖЕНИЯ С ЧЕТКО ВЫСТРОЕННЫМИ КОРИДОРАМИ И СТРОГОЙ ОРИЕНТАЦИЕЙ ПОМЕЩЕНИЙ ПО СТОРОНАМ СВЕТА БЫЛО ПРОСТО НЕВОЗМОЖНО.
ГРАФФИТИ НА СТЕНАХ КАМЕННЫХ БЛОКОВ НЕ ДОНЕСЛИ ДО СОВРЕМЕННОСТИ ИМЕН ГЕНИАЛЬНЫХ МАТЕМАТИКОВ.
Слайд 3ПОНЯТИЕ КВАДРАТНЫХ КОРНЕЙ ЧИСЛА ВОЗНИКЛО ОКОЛО 4 ТЫСЯЧ ЛЕТ НАЗАД В ВАВИЛОНЕ.
ПОНЯТИЕ КВАДРАТНЫХ КОРНЕЙ ЧИСЛА ВОЗНИКЛО ОКОЛО 4 ТЫСЯЧ ЛЕТ НАЗАД В ВАВИЛОНЕ.
ЕЩЕ В ВАВИЛОНЕ БЫЛИ СОСТАВЛЕНЫ ТАБЛИЦЫ КВАДРАТОВ ЧИСЕЛ И ВЕЛИЧИНЫ КВАДРАТНЫХ КОРНЕЙ ИЗ ЧИСЛА. ПРАВДА, ВЫЧИСЛЕНИЯ БЫЛИ ПРИБЛИЖЕННЫМИ. ПОДРОБНЫЙ МЕТОД ИЗВЛЕЧЕНИЯ КВАДРАТНЫХ КОРНЕЙ БЫЛ ОПИСАН ТОЛЬКО В 1 ВЕКЕ ДО Н.Э. ДРЕВНЕГРЕЧЕСКИМ УЧЕНЫМ ГЕРОНОМ АЛЕКСАНДРИЙСКИМ.
В ЭПОХУ ВОЗРОЖДЕНИЯ ЕВРОПЕЙСКИЕ МАТЕМАТИКИ ОБОЗНАЧАЛИ КОРЕНЬ ЛАТИНСКИМ СЛОВОМ RADIX (КОРЕНЬ), А ЗАТЕМ СОКРАЩЕНО БУКВОЙ R (ОТСЮДА ПРОИЗОШЕЛ ТЕРМИН «РАДИКАЛ», КОТОРЫМ ПРИНЯТО НАЗЫВАТЬ ЗНАК КОРНЯ). НЕКОТОРЫЕ НЕМЕЦКИЕ МАТЕМАТИКИ XV В. ДЛЯ ОБОЗНАЧЕНИЯ КВАДРАТНОГО КОРНЯ ПОЛЬЗОВАЛИСЬ ТОЧКОЙ.
ЭТУ ТОЧКУ СТАВИЛИ ПЕРЕД ЧИСЛОМ, ИЗ КОТОРОГО НУЖНО ИЗВЛЕЧЬ КОРЕНЬ. ПОЗДНЕЕ ВМЕСТО ТОЧКИ СТАЛИ СТАВИТЬ РОМБИК, ВПОСЛЕДСТВИИ ЗНАК И НАД ВЫРАЖЕНИЕМ, ИЗ КОТОРОГО ИЗВЛЕКАЕТСЯ КОРЕНЬ, ПРОВОДИЛИ ЧЕРТУ. ЗАТЕМ ЗНАК И ЧЕРТУ СТАЛИ СОЕДИНЯТЬ.
В ЭПОХУ ВОЗРОЖДЕНИЯ ЕВРОПЕЙСКИЕ МАТЕМАТИКИ ОБОЗНАЧАЛИ КОРЕНЬ ЛАТИНСКИМ СЛОВОМ RADIX (КОРЕНЬ), А ЗАТЕМ СОКРАЩЕНО БУКВОЙ R (ОТСЮДА ПРОИЗОШЕЛ ТЕРМИН «РАДИКАЛ», КОТОРЫМ ПРИНЯТО НАЗЫВАТЬ ЗНАК КОРНЯ). НЕКОТОРЫЕ НЕМЕЦКИЕ МАТЕМАТИКИ XV В. ДЛЯ ОБОЗНАЧЕНИЯ КВАДРАТНОГО КОРНЯ ПОЛЬЗОВАЛИСЬ ТОЧКОЙ.
ЭТУ ТОЧКУ СТАВИЛИ ПЕРЕД ЧИСЛОМ, ИЗ КОТОРОГО НУЖНО ИЗВЛЕЧЬ КОРЕНЬ. ПОЗДНЕЕ ВМЕСТО ТОЧКИ СТАЛИ СТАВИТЬ РОМБИК, ВПОСЛЕДСТВИИ ЗНАК И НАД ВЫРАЖЕНИЕМ, ИЗ КОТОРОГО ИЗВЛЕКАЕТСЯ КОРЕНЬ, ПРОВОДИЛИ ЧЕРТУ. ЗАТЕМ ЗНАК И ЧЕРТУ СТАЛИ СОЕДИНЯТЬ.
Слайд 4 Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого
Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого

равен а.
ОПРЕДЕЛЕНИЕ ЧТО ТАКОЕ КВАДРАТНЫЙ КОРЕНЬ
Арифметический квадратный корень из числа а обозначают √а.
Знак √ называют знаком арифметического квадратного корня или знаком радикала (от латинского слова radex — корень).
Выражение, стоящее под знаком корня, называют подкоренным выражением. Запись √а читают: квадратный корень из а (слово «арифметический» при чтении опускают).
Слайд 5СВОЙСТВА КОНЕЙ
СВОЙСТВА КОНЕЙ

Слайд 6СВОЙСТВО КОРНЕЙ
СВОЙСТВО КОРНЕЙ

Слайд 7СВОЙСТВО КОРНЕЙ
СВОЙСТВО КОРНЕЙ

- Предыдущая
ГК ПерспективаСледующая -
Омонимы Задача на знаходження суми
Задача на знаходження суми Теоремы о пределах. Нахождение пределов
Теоремы о пределах. Нахождение пределов Решение задач с параметрами
Решение задач с параметрами Умножение матрицы на число
Умножение матрицы на число Правила нахождения производных
Правила нахождения производных Сфера
Сфера krivye-vtorogo-poryadka (1)
krivye-vtorogo-poryadka (1) Контрольная работа по алгебре
Контрольная работа по алгебре Линейные уравнения. Решение задач с помощью линейных уравнений. 7 класс
Линейные уравнения. Решение задач с помощью линейных уравнений. 7 класс Методы решения системы трёх линейных уравнений с тремя неизвестными
Методы решения системы трёх линейных уравнений с тремя неизвестными Измеряй и сравнивай
Измеряй и сравнивай Прибавить и вычесть 2
Прибавить и вычесть 2 Признак перпендикулярности прямой и плоскости. 10 класс
Признак перпендикулярности прямой и плоскости. 10 класс Зимующие птицы. Дети 5 лет
Зимующие птицы. Дети 5 лет Повторение: Числа
Повторение: Числа Построение графиков функций с помощью производных
Построение графиков функций с помощью производных Первообразная. Интеграл. Площадь криволинейной трапеции
Первообразная. Интеграл. Площадь криволинейной трапеции Её величество Степень
Её величество Степень Презентация на тему Наглядная геометрия для начальной школы
Презентация на тему Наглядная геометрия для начальной школы  Л 9 Бесконечно большие функции и замечательные пределы
Л 9 Бесконечно большие функции и замечательные пределы Векторы в пространстве. Решение задач по готовым чертежам
Векторы в пространстве. Решение задач по готовым чертежам Теоремы Пифагора
Теоремы Пифагора Задачи на проценты
Задачи на проценты Сложение и вычитание алгебраических дробей с разными знаменателями. 8 класс
Сложение и вычитание алгебраических дробей с разными знаменателями. 8 класс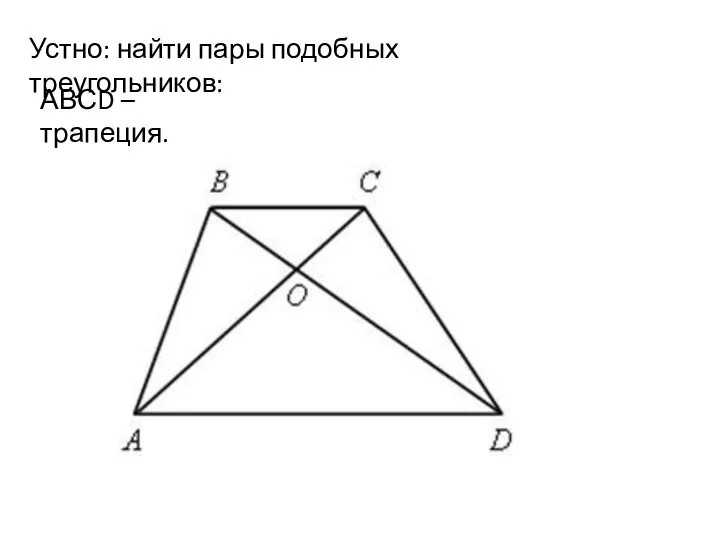 Признак подобия треугольников. Урок 32
Признак подобия треугольников. Урок 32 Теорема Пифагора
Теорема Пифагора Решение задач. Таблица умножения на 6. Кратное сравнение чисел
Решение задач. Таблица умножения на 6. Кратное сравнение чисел Простейшие комбинации
Простейшие комбинации