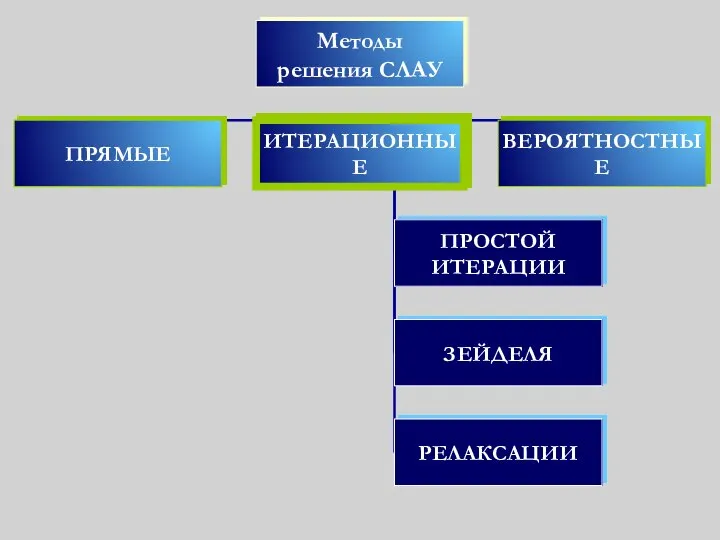
Численные методы решения СЛАУ (часть 2)

План
Погрешность прямых методов
Устойчивость по входным данным
Итерационные методы
Приведение СЛАУ к итерационному виду
Метод простой итерации
Метод Зейделя
Метод релаксации

Погрешность прямых методов решения СЛАУ
Источники ошибок:
ограниченность разрядной сетки ЭВМ;
погрешность представления исходных данных (коэффициентов системы A и (или) вектора правой части F).

Уточнение корней
Обозначим прибл. решение системы (1) через xi (i=1,2,…,n). Подставим это решение в исходную систему:
Ax = f.
Вычтем эти системы:
A(x – x )= f - f.
Обозначим через y = x – x, ε = f – f
невязка

Уточнение корней
Получим новую систему:
Ay=ε.
Решая ее, находим прибл. корни y.
Это решение используется для уточнения x:
x = x + y.
Этот процесс можно повторять.

Устойчивость по входным данным
Фактически вместо исходной системы при наличии погрешности исходных данных решается не система (1),
а «возмущенная система (2):
(1)
(2)

Устойчивость по входным данным
Необходимо оценить, как связаны погрешность решения ΔX=X*-X с абсолютными погрешностями коэффициентов матрицы ΔA=A*-A и свободных членов Δf=f*-f.
Это т.н. коэффициентная устойчивость и устойчивость по правой части.

Устойчивость по входным данным
Для оценки погрешности и устойчивости системы обратимся к основным характеристикам СЛАУ, известным из курса алгебры.
Напомним некоторые определения.

Определение 1. Норма вектора
Нормой вектора X называется неотрицательное число ||X|| такое, что

Определение 2. Норма матрицы
Нормой матрицы A называется неотрицательное число ||A|| такое, что

Виды норм
матрицы:
вектора:
кубическая
октаэдрическая
сферическая

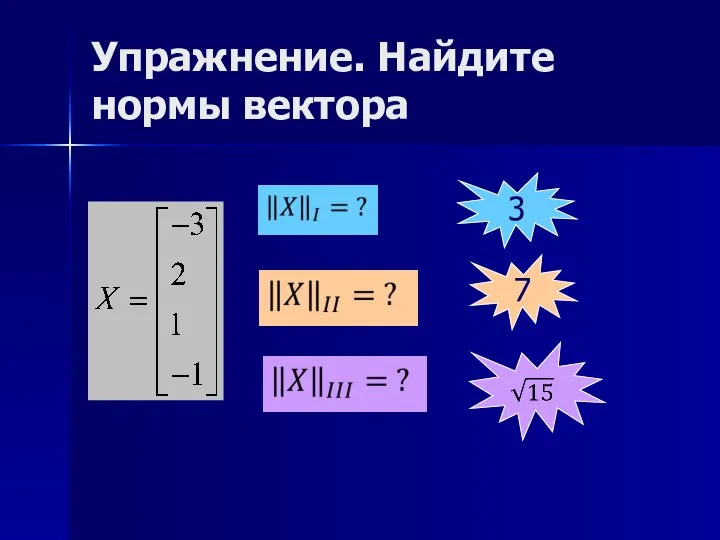
Упражнение. Найдите нормы вектора
3
7

Упражнение. Найдите нормы матриц
кубическую:
октаэдрическую:
сферическую:

Погрешность решения
Относительная погрешность решения связана с погрешностью правой части следующим образом:
Константа пропорциональности MA- число обусловленности матрицы.

Число обусловленности матрицы
Обусловленность – это внутреннее свойство матрицы, не связанное со способом решения системы уравнений. Если это число велико, матрица называется плохо обусловленной. Решение СЛАУ считается ненадежным, если

Примеры
Классическим примером плохо обусловленной матрицы является матрица Гильберта с элементами
Уже при n=8 MH≥1010.

Точное решение:
x=1, y=1.
Небольшое отклонение в исходных данных резко меняет решение:
Эта система дает решение x=3.000, y=-1.0203.
Число обусловленности матрицы A в данном случае порядка 40 000.

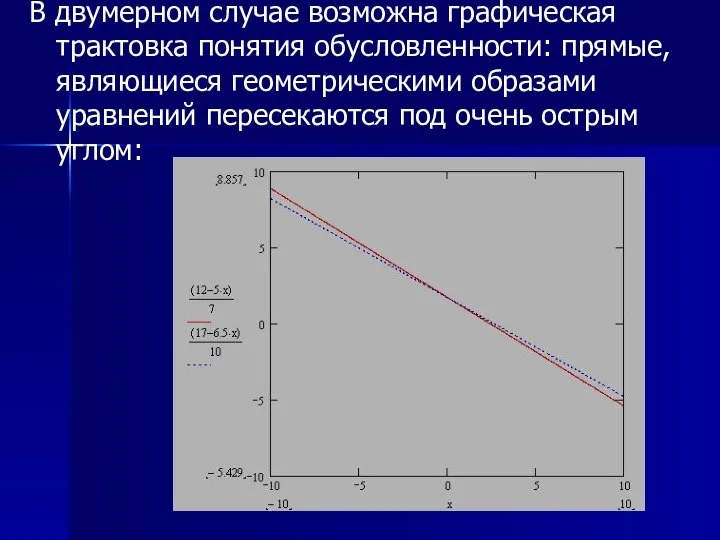
В двумерном случае возможна графическая трактовка понятия обусловленности: прямые, являющиеся геометрическими образами уравнений пересекаются под очень острым углом:

Графическая трактовка понятия обусловленности
Небольшое искажение данных (параллельный перенос при изменении свободных членов, поворот при возмущении матрицы коэффициентов) приводит к значительному перемещению точки пересечения (геометрического образа решения).

Какие из систем плохо обусловлены?
Ответ: 1), 4)

Число обусловленности
На практике для нахождения числа обусловленности пользуются его свойством:
где λmax и λmin – наибольшее и наименьшее по модулю собственные числа матрицы A.

Обусловленность матрицы
Решающую роль в обусловленности играет не близость к 0 определителя, а разброс собственных значений матрицы.

Погрешность решения
Знание числа обусловленности позволяет оценить и погрешности округления на ЭВМ. Если каждая компонента вектора правой части округляется с относительной погрешностью O(2-m), где m – разрядность сетки ЭВМ, то решение задачи (1) не может быть найдено с точностью, большей, чем MAO(2-m).

Обусловленность систем
Решение плохо обусловленных систем – некорректная задача. Чтобы преодолеть некорректность используют метод регуляризации, основанный на привлечении дополнительной информации о решении.

Итерационные методы
В случае произвольной матрицы А и достаточно большого числа n решение системы (1) с помощью прямых методов затруднительно. В этом случае применяются итерационные методы.

Приведение системы к итерационному виду
Для этого систему (1) переписываем в виде, удобном для итерационного процесса:
В матричном виде:
(2)

Пример. Пусть дана система
Приведение системы к итерационному виду

Способ 1. Поделив каждое уравнение на соответствующий диагональный элемент (если они не равны нулю) и решив уравнения относительно диагональных переменных, получим:
(*)
Приведение системы к итерационному виду

Способ 2. Вычленим единицу из каждого диагонального элемента и выразим полученные неизвестные:
Эти системы эквивалентны, т.е. имеют одинаковые решения.
(**)
Приведение системы к итерационному виду

Все итерационные методы решения системы, приведённой к итерационному виду, состоят в том, что выбирается некоторое начальное приближение (вектор X0), которое подставляется в правую часть итерационной системы. В левой части тогда получаем решение на первой итерации, затем подставляем его в правую часть - и т. д. Последовательность векторов строится до тех пор, пока не будет достигнута заданная точность:

Итерационные методы различаются только по способу построения последовательности.
Формулы метода простой итерации:
Метод простой итерации

Метод простой итерации
Прерываем итерационный процесс, когда выполнится условие достижения заданной точности.
Для первой приведенной системы (*) из примера последовательность приближений решения:
x(0)=(0,0,0)
x(1)=(0.8,0.5,0.5)
x(2)=(0.85,0.55,0.425)
……………………..

Достаточное условие сходимости метода простой итерации
Рассмотрим, при каком условии сходится построенная последовательность векторов. Сходимость векторов рассматривается покоординатная, т.е. расстояние между векторами вычисляется по формуле:

Теорема. Итерационный процесс сходится к единственному решению, если какая-либо каноническая норма матрицы
Нормой квадратной матрицы А называется вещественное число , удовлетворяющее следующим условиям:
Для канонической нормы выполняется еще два дополнительных условия:

Доказательство
Запишем k-ое приближение итерационной последовательности
через все предыдущие

Т.к. , то
Используем формулу, аналогичную сумме бесконечной убывающей геометрической прогрессии со знаменателем q<1:

Т.о., предельный вектор X является решением итерационной системы. Теорема доказана.

Следствие 1. Итерационный процесс сходится, если для системы (2) выполняется любое из неравенств:
1)
2)
3)
кубическая
октаэдрическая
сферическая

Следствие 2. Для исходной системы (1) достаточным условием сходимости метода итераций является одно из:
В приведенном примере итерации сходятся для системы (*) согласно следствия 1, для системы (**) - следствия 2.
или

Проверка условий сходимости
Приведем систему к диагональному преобладанию путем линейной комбинации строк
У1 = У1+У2
У2 = 2*У1 – У2
У3 = У1-2*У2+У3

Оценка погрешности метода простой итерации
Если матрица α удовлетворяет условию
, то для оценки погрешности приближенного вектора
Х(k) имеет место формула:

Метод Зейделя
В этом методе для нахождения i-ой компоненты решения на (к+1)-ой итерации используются уже найденные на (к+1) значения

Метод Зейделя
Таким образом, при вычислении очередной компоненты xi используются вычисленные x1, x2, …, xi-1 с новой итерации, в то время как в методе простой итерации используются все значения с предыдущей.

В матричном виде метод Зейделя можно записать в следующем виде:
D – диагональ матрицы α

Условие сходимости
Достаточное условие сходимости практически аналогично методу простой итерации. Однако, в некоторых случаях оно менее строгое, т.е. метод Зейделя может сходиться, когда метод простой итерации расходится. Обычно метод Зейделя дает лучшую скорость сходимости, чем метод простой итерации.

Условие сходимости метода Зейделя
Необходимое и достаточное условие: модули всех корней уравнения (3) должны быть меньше 1.

Метод релаксации
Метод релаксации является обобщением метода Зейделя. Алгоритм построения итерационной последовательности в данном случае имеет вид:
где ω=const>0 – параметр релаксации, управляющий скоростью сходимости итерационного процесса.