Содержание
- 2. Определение функции Определение 1. Функцией называют такую зависимость переменной y от переменной х, при которой каждому
- 3. Область определения функции Определение 2. Множество всех значений аргумента х называют областью определения функции и обозначают
- 4. Область значений функции Определение 3. Множество всех значений функции у называют областью значений функции и обозначают
- 5. Свойства функций Определение 4. Функцию y=f(x) называют возрастающей на промежутке, если большему значению аргумента соответствует большее
- 6. Определение 5. Функцию y=f(x) называют убывающей на промежутке, если большему значению аргумента соответствует меньшее значение функции
- 7. Нули функции Определение 6. Значение аргумента, при которых функция обращается в нуль, называют нулями функции
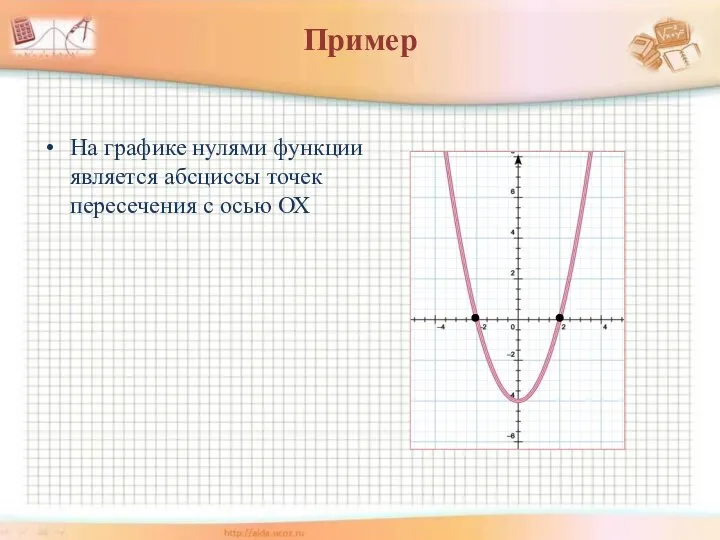
- 8. Пример На графике нулями функции является абсциссы точек пересечения с осью ОХ
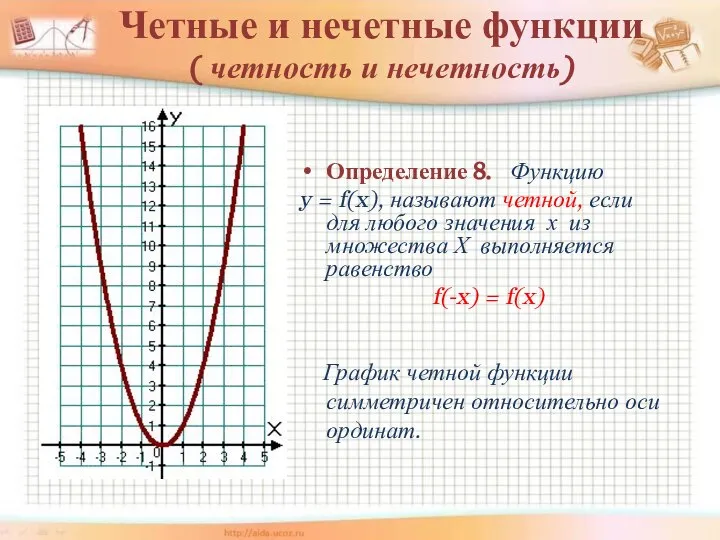
- 9. Четные и нечетные функции ( четность и нечетность) Определение 8. Функцию y = f(x), называют четной,
- 11. Скачать презентацию






 Стереометрия 1. ЕГЭ
Стереометрия 1. ЕГЭ Проценты
Проценты Решение функции
Решение функции Проекты сезона 2020-21
Проекты сезона 2020-21 Объёмные и плоские геометрические фигуры
Объёмные и плоские геометрические фигуры Неравенства с логарифмами
Неравенства с логарифмами ТРАПЕЦІЯ
ТРАПЕЦІЯ Тренировка интеллекта
Тренировка интеллекта Задачи с параметрами
Задачи с параметрами Системы линейных алгебраических уравнений
Системы линейных алгебраических уравнений Правильные многогранники
Правильные многогранники Презентация на тему Второй признак равенства треугольников 7 класс
Презентация на тему Второй признак равенства треугольников 7 класс  Касательная к окружности
Касательная к окружности Умножение и деление десятичных дробей. Самостоятельная работа
Умножение и деление десятичных дробей. Самостоятельная работа Однородные тригонометрические уравнения
Однородные тригонометрические уравнения Линейные однородные дифференциальные уравнения с постоянными коэффициентами
Линейные однородные дифференциальные уравнения с постоянными коэффициентами Решение уравнений с модулем
Решение уравнений с модулем Скалярное произведение векторов. Решение задач на вычисление скалярного произведения векторов
Скалярное произведение векторов. Решение задач на вычисление скалярного произведения векторов Треугольник и его виды
Треугольник и его виды Устный счет в пределах 100. Тренажер
Устный счет в пределах 100. Тренажер Движения
Движения Контрольная работа. Умножение и деление
Контрольная работа. Умножение и деление Презентация на тему Задачи на построение (7 класс)
Презентация на тему Задачи на построение (7 класс)  Формулы сокращенного умножения
Формулы сокращенного умножения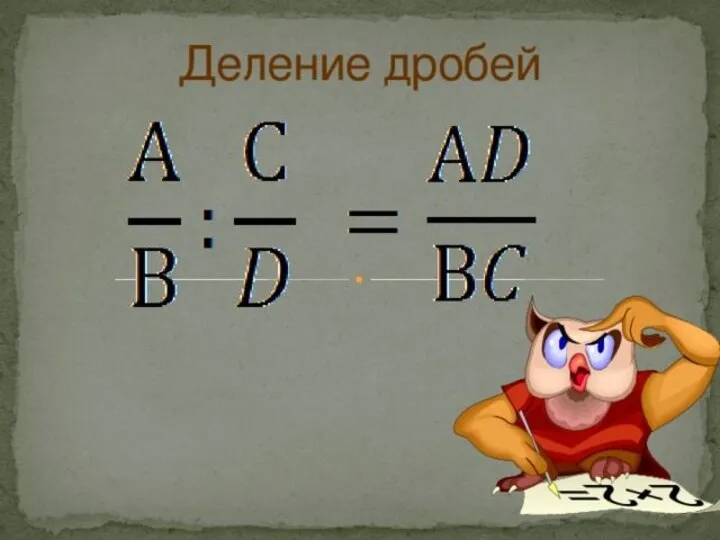 Деление дробей
Деление дробей Своя игра по теме: Сложение и вычитание дробей
Своя игра по теме: Сложение и вычитание дробей Равносильность уравнений и неравенств системам. Урок по алгебре и началам анализа 11 класс
Равносильность уравнений и неравенств системам. Урок по алгебре и началам анализа 11 класс Применение определенного интеграла при решении геометрических и физических задач
Применение определенного интеграла при решении геометрических и физических задач