Слайд 210.2
Последовательности можно складывать, вычитать, умножать и делить:
Последовательность {xn} называется возрастающей (убывающей), если

для любого номера n выполняется неравенство xn+1 > xn (xn+1 < xn).
Слайд 310.3
Арифметическая прогрессия

Слайд 410.4
Геометрическая прогрессия

Слайд 510.5
Или
Геометрически определение предела можно сформулировать следующим образом: число а есть предел последовательности

{xn}, если какова бы ни была ε - окрестность точки а, начиная с некоторого номера все точки xn попадут в эту окрестность, т.е. вне интервала (а – ε, а + ε) останется лишь конечное число членов последовательности.
Если последовательность имеет пределом число а, то говорят, что последовательность сходится к числу а и записывают так:
иначе последовательность – расходится.
Сходящаяся последовательность имеет только один предел!








 Площадь прямоугольника
Площадь прямоугольника Алгоритм решения линейных уравнений
Алгоритм решения линейных уравнений Презентация на тему Сечения многогранников
Презентация на тему Сечения многогранников  Основы логики
Основы логики Решение иррациональных уравнений
Решение иррациональных уравнений Уравнение прямой. 9 класс
Уравнение прямой. 9 класс Решение задач. Многогранники. Тела вращения
Решение задач. Многогранники. Тела вращения Натуральные числа. Викторина
Натуральные числа. Викторина Применение графика производной к исследованию функции
Применение графика производной к исследованию функции Треугольник. Первый признак равенства треугольников
Треугольник. Первый признак равенства треугольников Презентация на тему Предел переменной величины
Презентация на тему Предел переменной величины  Презентация на тему Логарифмическая линия в ЕГЭ - 2011
Презентация на тему Логарифмическая линия в ЕГЭ - 2011  Кругові приклади
Кругові приклади Понятие логарифма
Понятие логарифма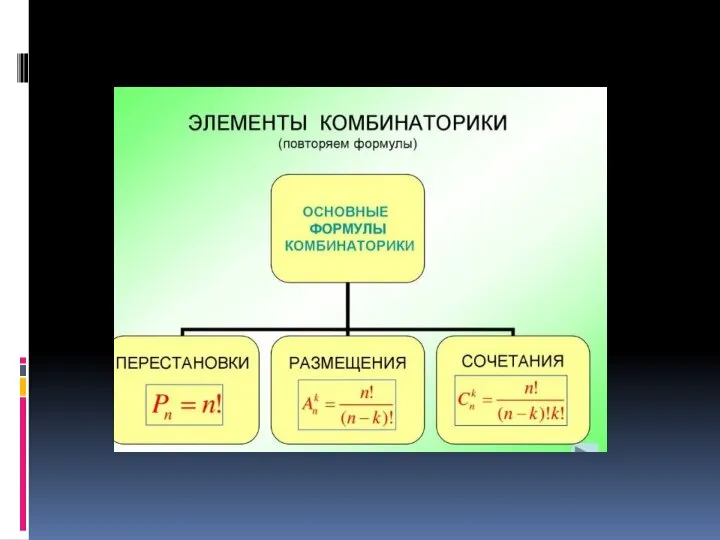 Основные понятия комбинаторики
Основные понятия комбинаторики График функции у = ах 2 + bх + qс
График функции у = ах 2 + bх + qс Решение задач на составление линейных алгоритмов
Решение задач на составление линейных алгоритмов Векторные задачи 1-го типа
Векторные задачи 1-го типа Применение игровых технологий на уроках математики в условиях внедрения ФГОС
Применение игровых технологий на уроках математики в условиях внедрения ФГОС Методы измерения физических величин
Методы измерения физических величин Определение перемещения
Определение перемещения Решение задач. 1 класс
Решение задач. 1 класс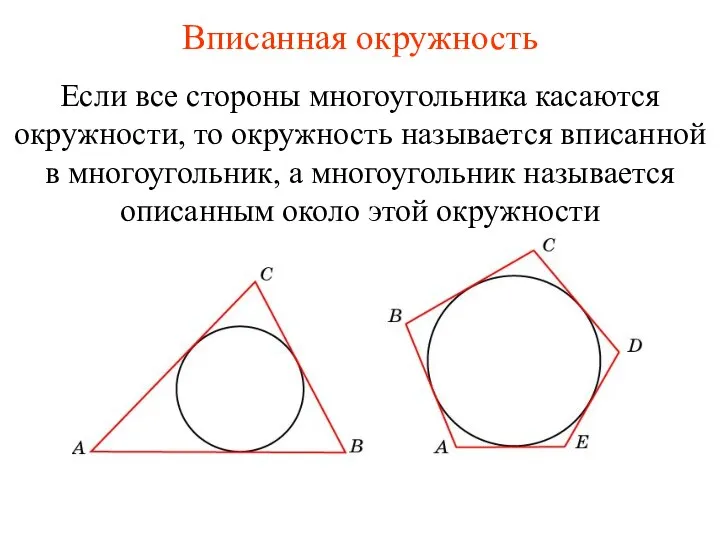 Вписанная окружность
Вписанная окружность Четные и нечётные функции
Четные и нечётные функции Таков многогранник
Таков многогранник Перпендикуляр и наклонная. Угол между прямой и плоскостью
Перпендикуляр и наклонная. Угол между прямой и плоскостью Сечение вокруг нас
Сечение вокруг нас Умножение дробей
Умножение дробей