Слайд 2Deterministic finite automata
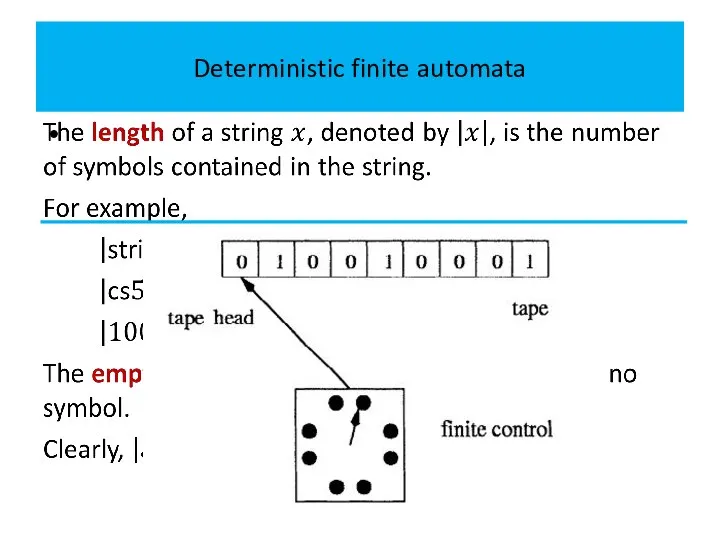
Deterministic finite automaton (DFA) consists of three parts: a tape,
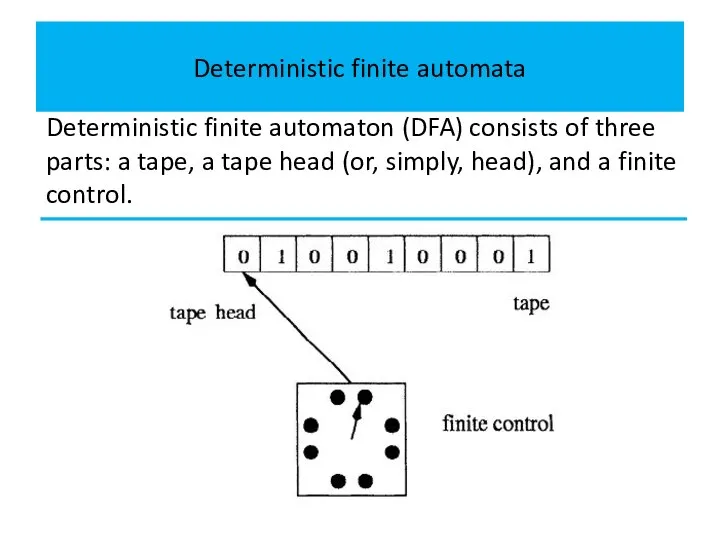
a tape head (or, simply, head), and a finite control.
Слайд 3Deterministic finite automata
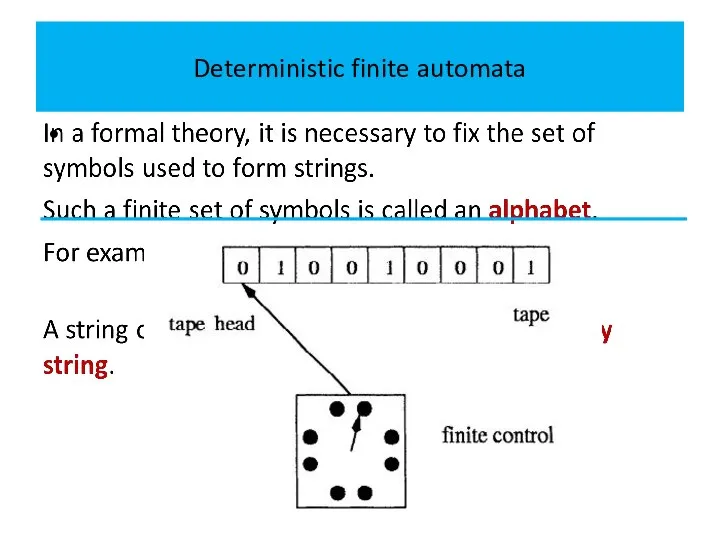
Слайд 4Deterministic finite automata
The tape head scans the tape, reads symbols from the
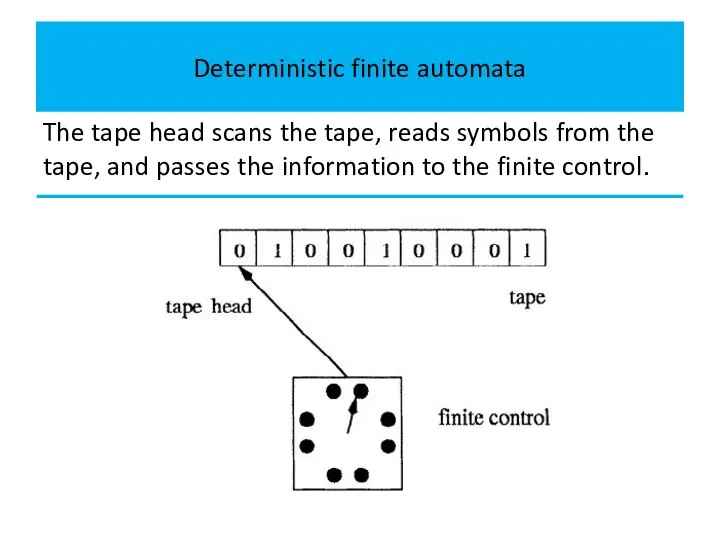
tape, and passes the information to the finite control.
Слайд 5Deterministic finite automata
At each move of the DFA, the head scans one
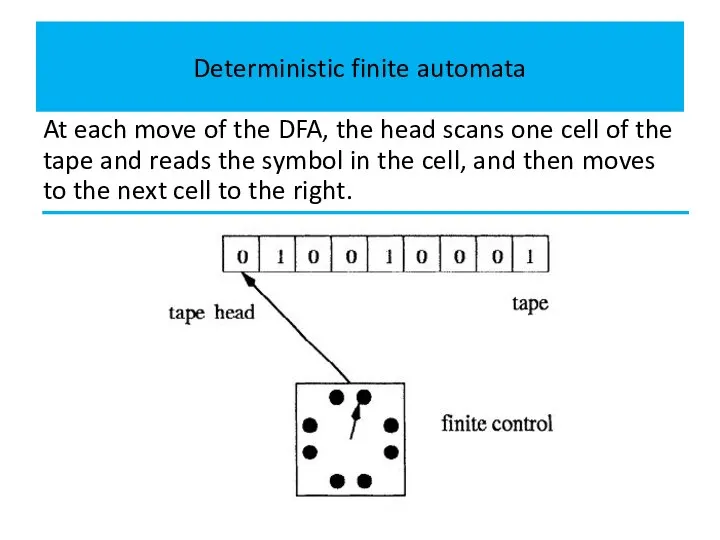
cell of the tape and reads the symbol in the cell, and then moves to the next cell to the right.
Слайд 6Deterministic finite automata
Слайд 7Deterministic finite automata
Then, it determines, from the current state and the symbol
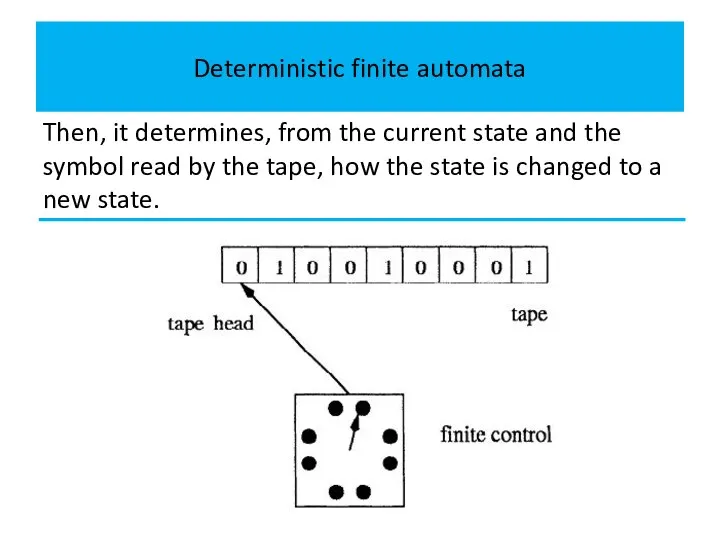
read by the tape, how the state is changed to a new state.
Слайд 8Deterministic finite automata

Слайд 9Deterministic finite automata

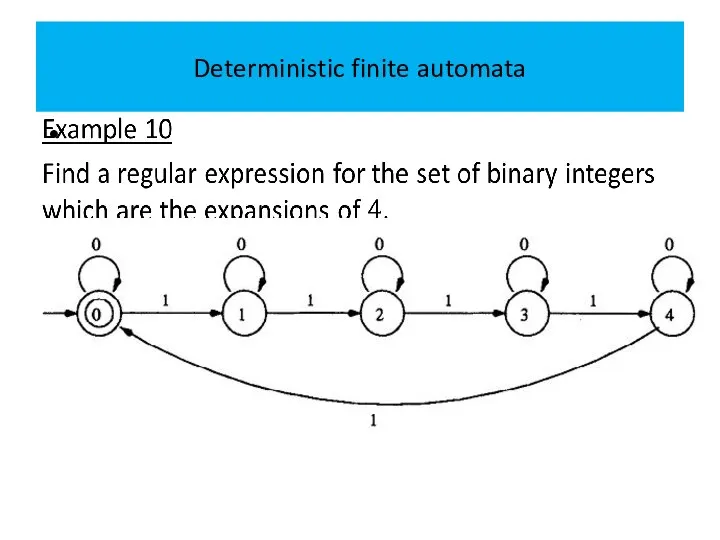
Слайд 11Deterministic finite automata
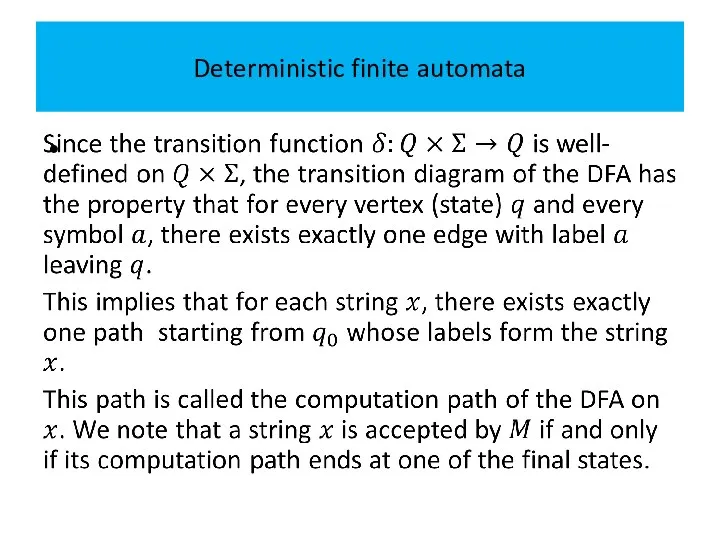
When the DFA halts, it accepts the input string if

it halts in one of the final states.
Otherwise, the input string is rejected.
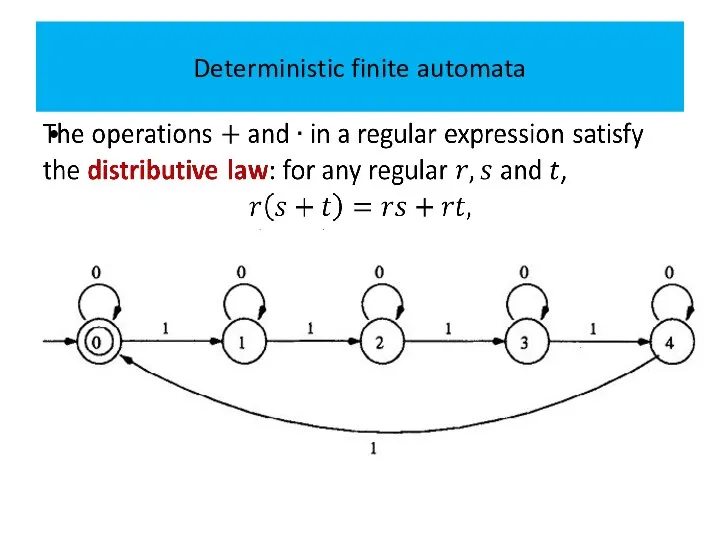
Слайд 13Deterministic finite automata
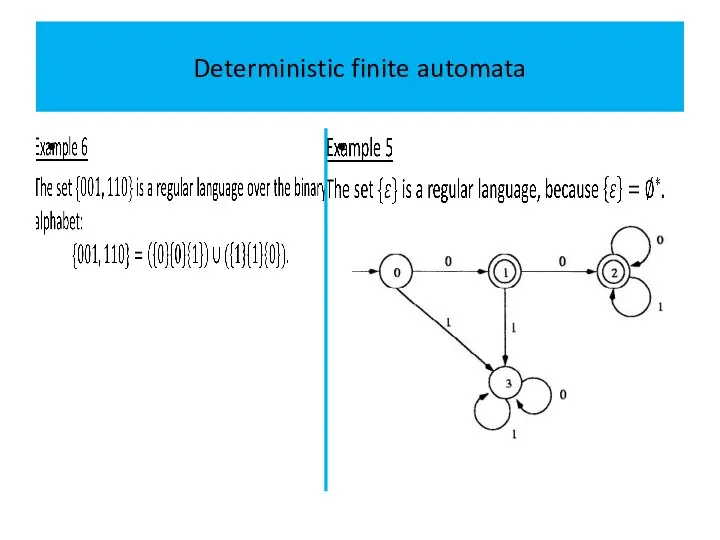
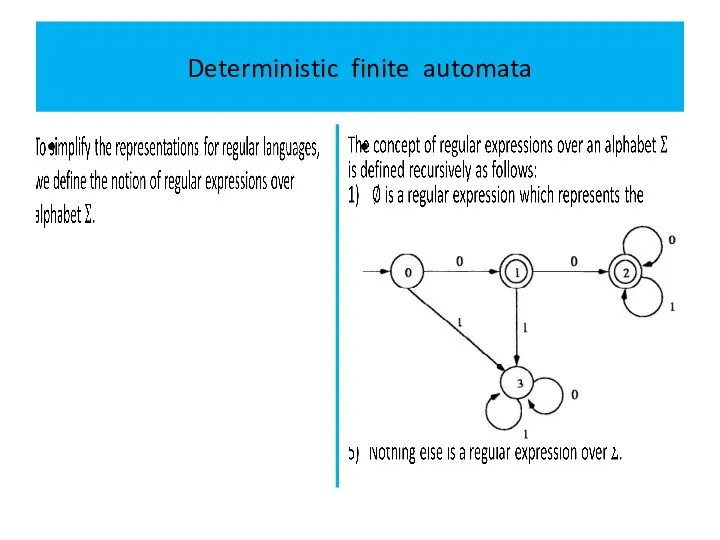
The transition diagram of a DFA is an alternative way

to represent the DFA.
Слайд 26Nondeterministic finite automata

Слайд 27Nondeterministic finite automata

Слайд 28Nondeterministic finite automata

Слайд 29Nondeterministic finite automata

Слайд 30Nondeterministic finite automata

Слайд 31Nondeterministic finite automata

Слайд 32Nondeterministic finite automata
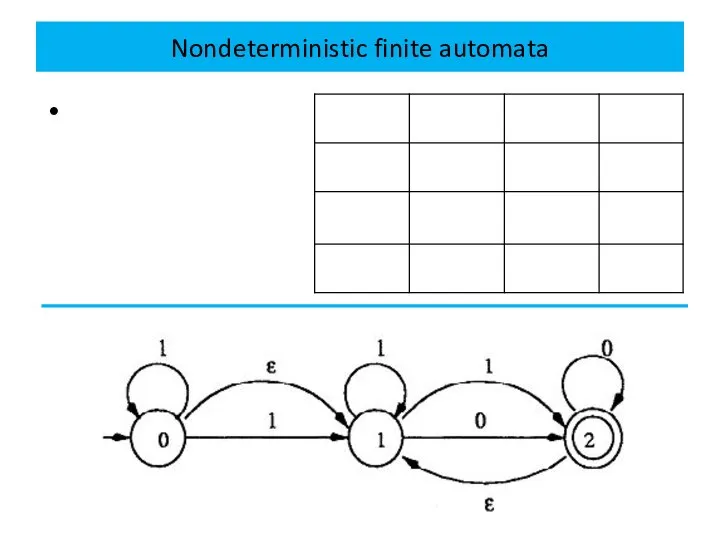
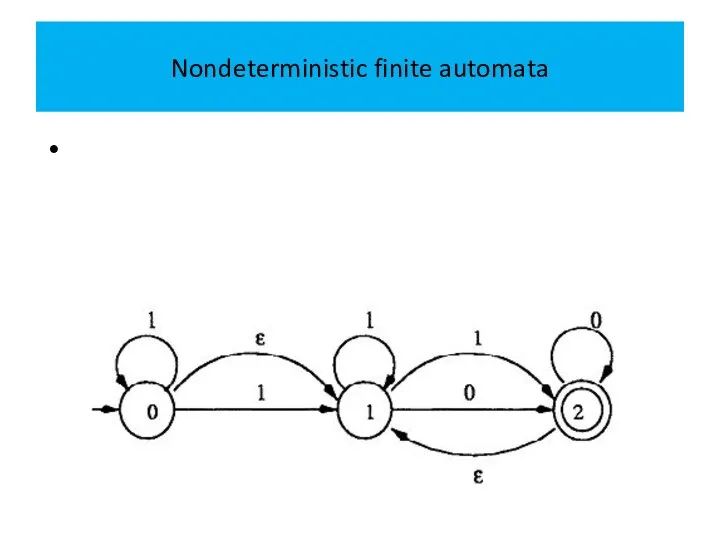
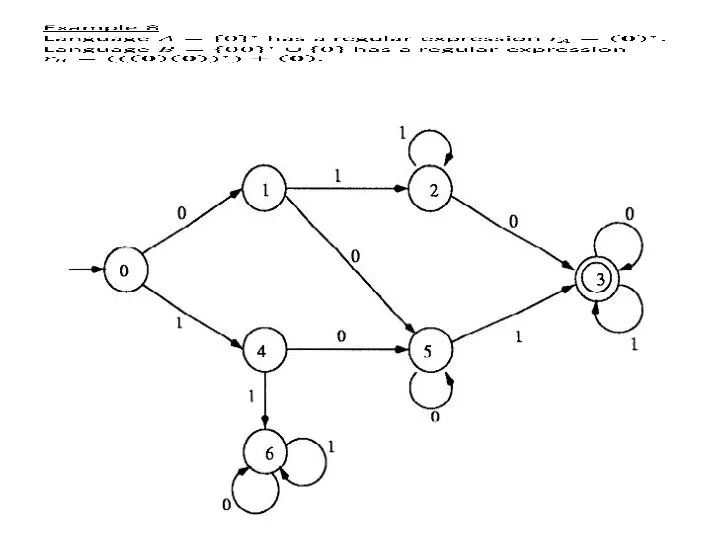
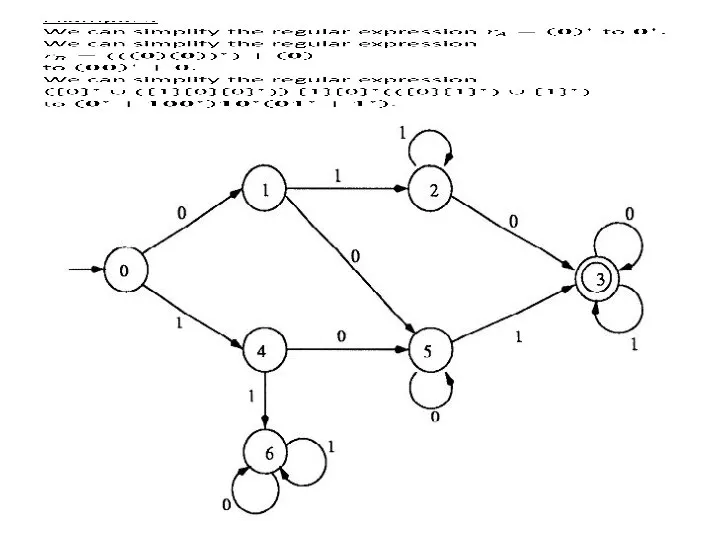
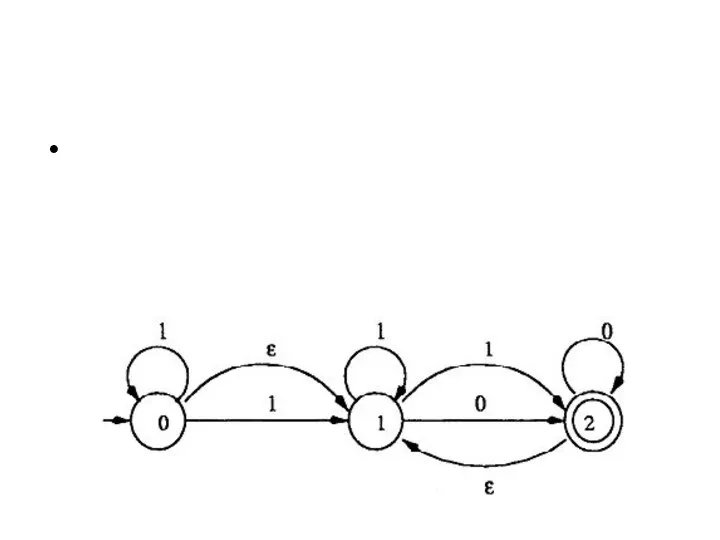
NFA’s, like DFA’s, can also be represented by transition

diagrams.
In the transition diagram, we still use a vertex to represent a state and a labeled edge to represent a move, except that we allow multiple edges from one vertex to other vertices with the same label.
Слайд 33Nondeterministic finite automata

Слайд 34Nondeterministic finite automata
Слайд 35Nondeterministic finite automata

Слайд 36Nondeterministic finite automata
Слайд 38Nondeterministic finite automata

Слайд 40Nondeterministic finite automata
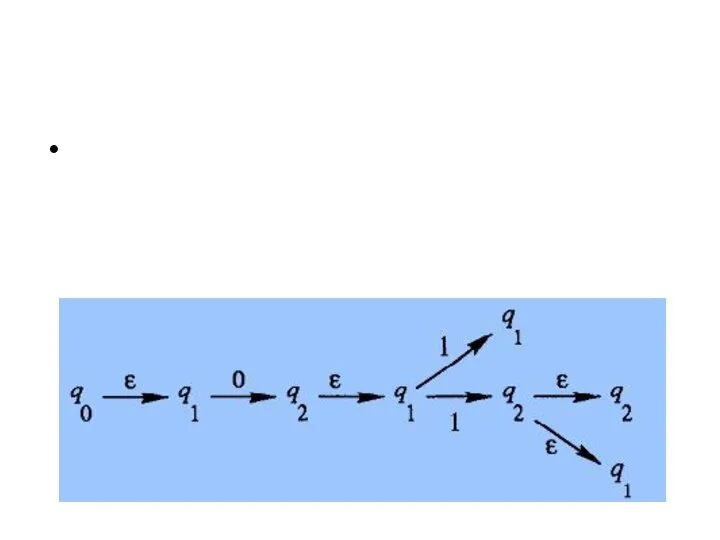
Some of these computation paths lead to final states

and some do not.
Слайд 41Nondeterministic finite automata





























 Задания по математике (5 класс, часть 3)
Задания по математике (5 класс, часть 3) Задания Незнайки
Задания Незнайки Алгоритм как один из приемов в формировании учебно-познавательной компетенции на уроках математики
Алгоритм как один из приемов в формировании учебно-познавательной компетенции на уроках математики Решение задач и уравнений
Решение задач и уравнений Нелинейные уравнения и системы нелинейных алгебраических уравнений. Лекция 4
Нелинейные уравнения и системы нелинейных алгебраических уравнений. Лекция 4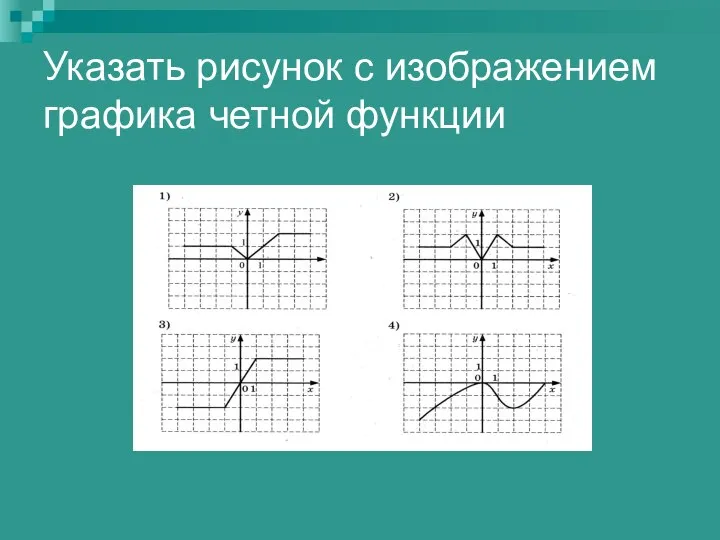 Указать рисунок с изображением графика четной функции
Указать рисунок с изображением графика четной функции В гостях у геометрических фигур
В гостях у геометрических фигур Объем прямоугольного параллелепипеда. Объем прямой призмы
Объем прямоугольного параллелепипеда. Объем прямой призмы Реши примеры устно. 2 класс
Реши примеры устно. 2 класс Признаки подобия треугольников
Признаки подобия треугольников Линейная функция. Работа по графику
Линейная функция. Работа по графику Координаты вектора в пространстве. 12 кл
Координаты вектора в пространстве. 12 кл Дополняем до круглого числа
Дополняем до круглого числа Графики функций
Графики функций Окружность. Методическая разработка урока
Окружность. Методическая разработка урока Решение уравнений. Подготовка к ОГЭ
Решение уравнений. Подготовка к ОГЭ Презентация на тему Натуральные числа 5 класс
Презентация на тему Натуральные числа 5 класс  Математический КВН. 6 класс
Математический КВН. 6 класс Презентация на тему Факториал 9 класс
Презентация на тему Факториал 9 класс  Метод координат на плоскости
Метод координат на плоскости Ряд Тейлора функции многих переменных. Лекция 19
Ряд Тейлора функции многих переменных. Лекция 19 Откуда к нам пришли отрицательные числа? Сказка бабушки Тортилы
Откуда к нам пришли отрицательные числа? Сказка бабушки Тортилы Значение логического выражения (тема № 3)
Значение логического выражения (тема № 3) Математическое обеспечение (МО) цифрового (автоматизированного) проектирования
Математическое обеспечение (МО) цифрового (автоматизированного) проектирования Зачёт по таблице умножения
Зачёт по таблице умножения Сравнение натуральных чисел
Сравнение натуральных чисел Движение в пространстве
Движение в пространстве Промежуточная аттестация по геометрии
Промежуточная аттестация по геометрии