Слайд 2Высказывания
Предложение, о котором имеет смысл говорить, что оно является истинным или ложным,

называют высказыванием.
Являются ли высказываниями предложения?
«Волга впадает в Черное море»
«2+2=4»
«Который час?»
«Мойте руки перед едой!»
«Земля – единственная обитаемая планета во Вселенной»
«Это высказывание – ложное»
Слайд 3Значение истинности высказывания

Слайд 4Элементарные и сложные высказывания
Если никакая часть высказывания сама по себе не является

высказыванием, то высказывание называют элементарным или исходным.
Сложным называют высказывание, допускающее разделение его на другие высказывания.
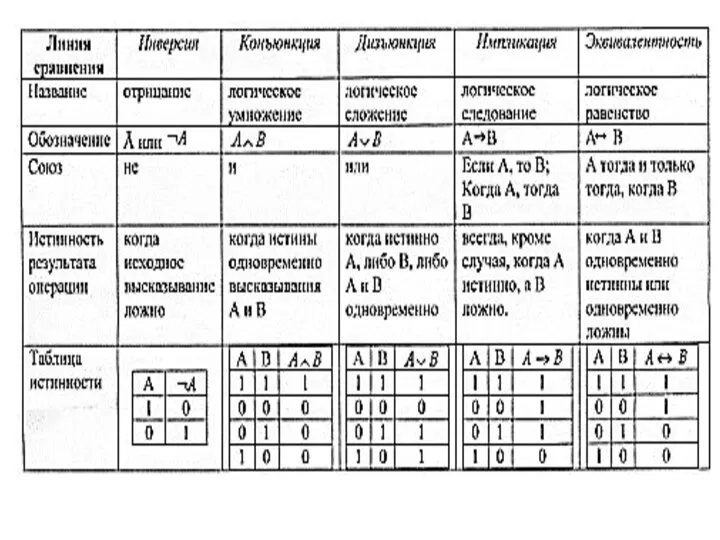
Слайд 5Операции над высказываниями
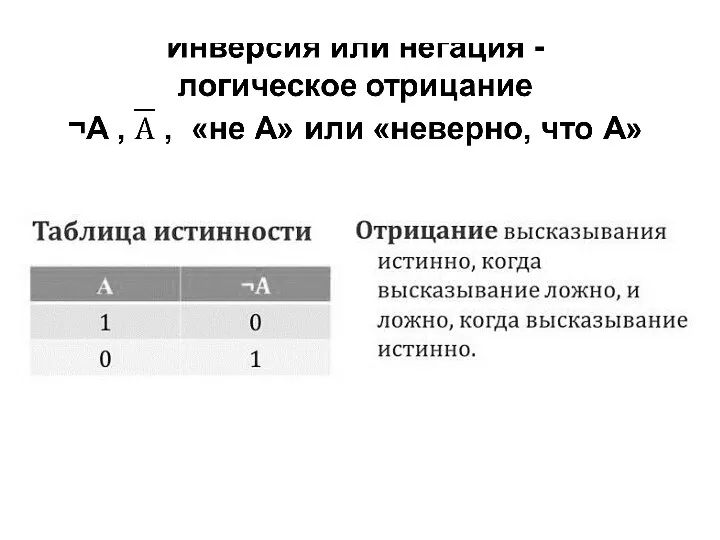
1. Инверсия или негация (логическое отрицание)
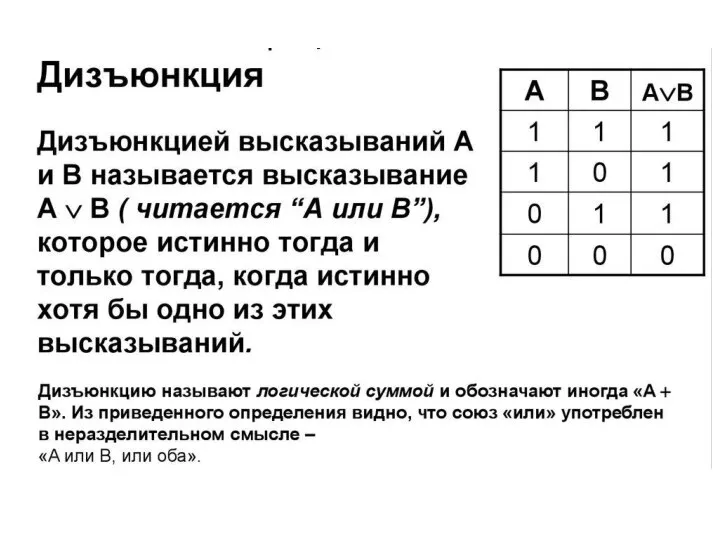
2. Дизъюнкция (логическое сложение)
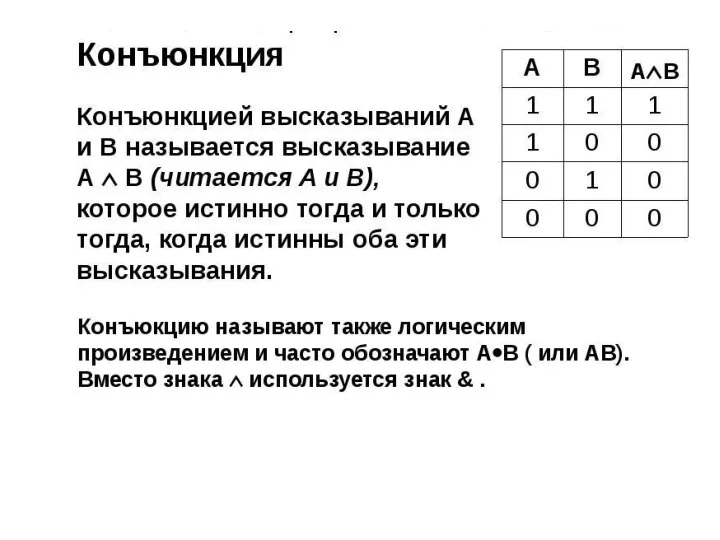
3.

Конъюнкция (логическое умножение)
4. Импликация (логическое следствие)
5. Эквивалентность или эквиваленция (логическое равенство)
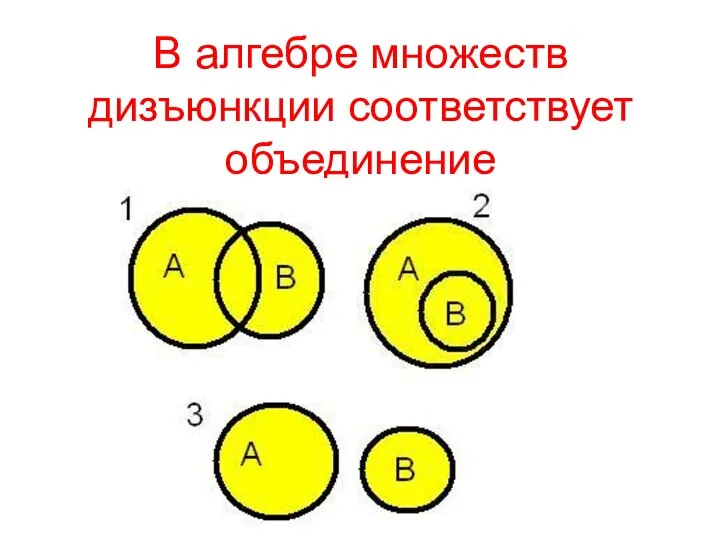
Слайд 9В алгебре множеств дизъюнкции соответствует объединение
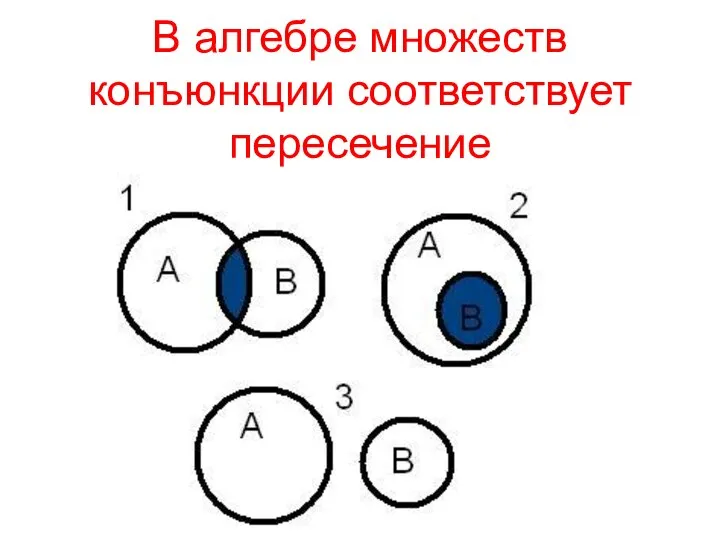
Слайд 11В алгебре множеств конъюнкции соответствует пересечение
Слайд 13Эквиваленция
(логическая равносильность)
Эквиваленцией двух высказываний называется новое высказывание, которое истинно тогда и только

тогда, когда оба высказывания одновременно истинны либо ложны.
Читается «А тогда и только тогда, когда В».
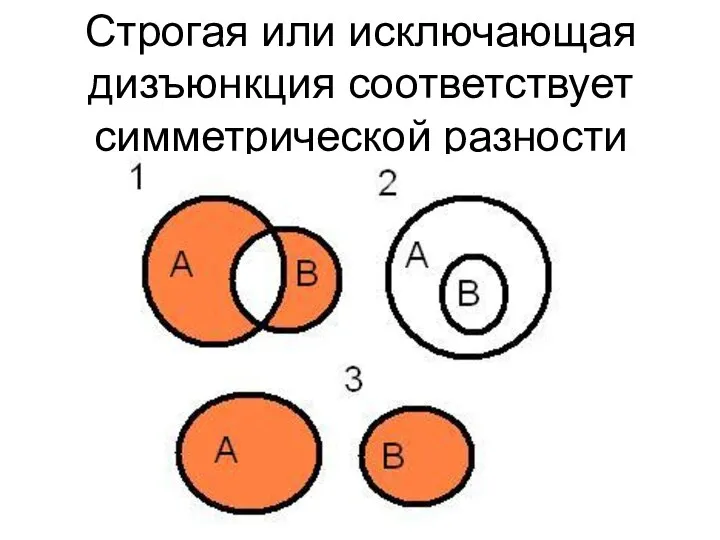
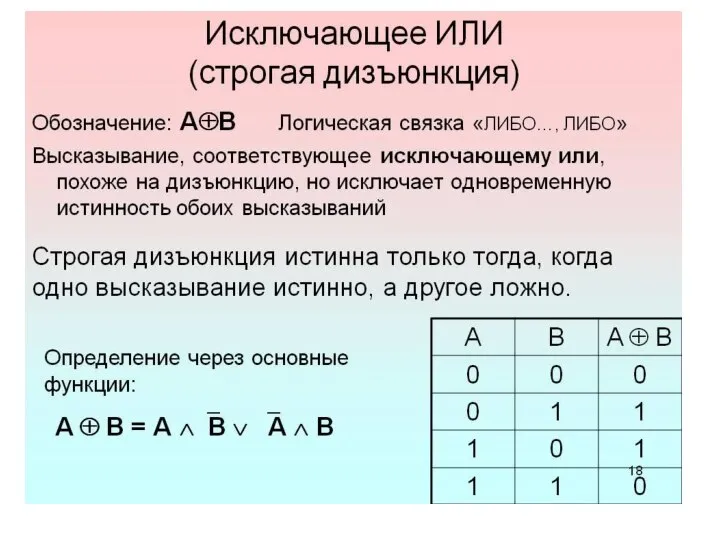
Слайд 15Строгая или исключающая дизъюнкция соответствует симметрической разности
Слайд 17Основные законы логики
1. Закон тождества
2. Закон непротиворечия
3. Закон исключения третьего
4. Закон отрицания

отрицания
Слайд 18Закон тождества
Всякое высказывание тождественно самому себе:
А = А

Слайд 22Пример задачи
Трое подозреваемых в преступлении Иванов, Петров и Сидоров дали следующие показания:

Иванов сказал: «Если виновен Сидоров, то и Петров тоже виновен».
Петров сказал: «Виновен либо Иванов, либо Сидоров, но не оба».
Сидоров сказал: «Я не виновен, а виновен Петров».
Слайд 23Построить таблицу истинности каждого высказывания и по ней определить:
а) Кто виновен,

если все говорят правду?
б) Кто виновен, если все лгут? в) Кто лжет, если все виновны?
г) Кто лжет, если все невиновны?
д) Кто виновен, если виновные лгут, а невиновные говорят правду?
Слайд 24Введем простые высказывания: А={виновен Иванов};
В={виновен Петров};
С={виновен Сидоров}.

Слайд 26Составляем таблицу истинности каждого высказывания:
А ⊕ С
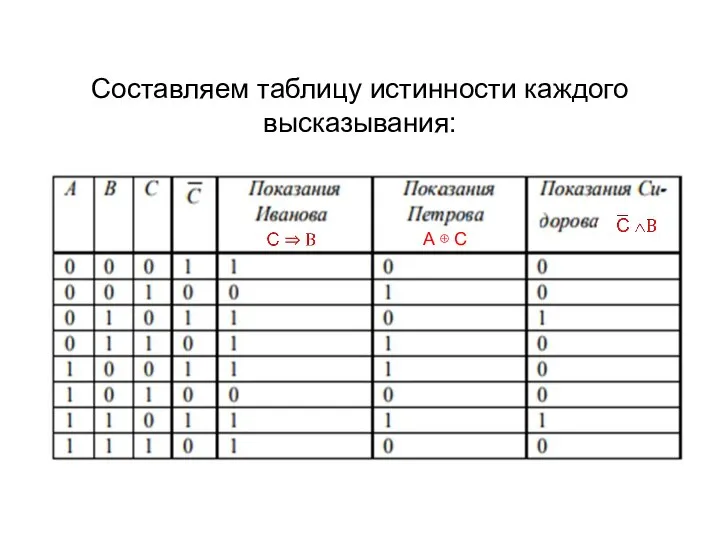
Слайд 27а) Если все говорят правду, то в показаниях (последние три столбца) должны

быть три единицы. Такому условию соответствует предпоследняя строка, из которой по значениям в первых трех столбцах (1,1,0) делаем вывод, что Иванов и Петров виновны, а Сидоров нет.
Слайд 28б) Если все лгут, то в показаниях должны быть три нуля. Такому

условию соответствует шестая строка, из которой по значениям в первых трех столбцах делаем вывод, что Иванов и Сидоров виновны, а Петров нет.
Слайд 29в) Условию того, что все виновны, соответствует последняя строка, у которой в

первых трех столбцах все единицы. По значениям показаний (последние три столбца) видно, что Иванов говорит правду, а Петров и Сидоров лгут
Слайд 30г) Условию того, что все невиновны, соответствует первая строка, у которой в

первых трех столбцах все нули. По значениям показаний видно, что Иванов говорит правду, а Петров и Сидоров лгут.
























 Аттестационная работа. Решение сложных задач по математике
Аттестационная работа. Решение сложных задач по математике Развитие учебных навыков через применение наглядных пособий и перевода математических задач в практическую плоскость
Развитие учебных навыков через применение наглядных пособий и перевода математических задач в практическую плоскость Соотношение величин
Соотношение величин Методы обработки данных и способы их представления в научном исследовании
Методы обработки данных и способы их представления в научном исследовании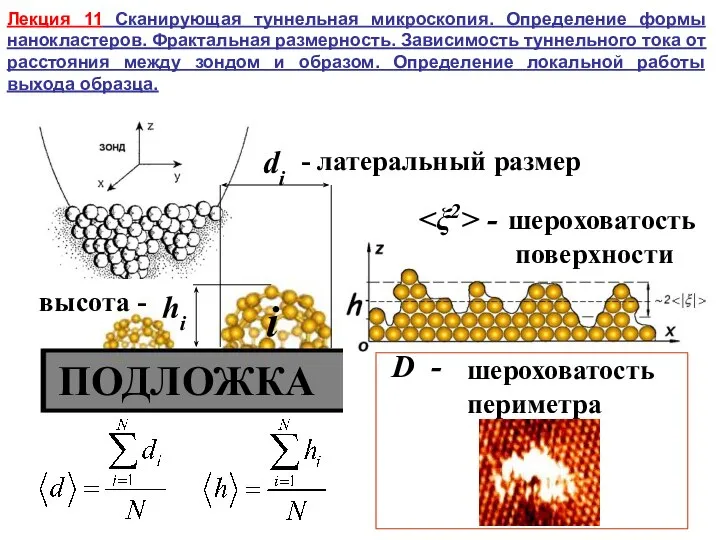 Сканирующая туннельная микроскопия. Определение формы нанокластеров. Фрактальная размерность
Сканирующая туннельная микроскопия. Определение формы нанокластеров. Фрактальная размерность Начальные сведения о задачах оптимизации
Начальные сведения о задачах оптимизации Юный математик
Юный математик Параллельные и перпендикулярные прямые
Параллельные и перпендикулярные прямые Первообразная. 11 класс
Первообразная. 11 класс Экстремум. Условный экстремум функции 2 переменных
Экстремум. Условный экстремум функции 2 переменных Кривые второго порядка
Кривые второго порядка Теорема Пифагора. Урок геометрии в 8 классе
Теорема Пифагора. Урок геометрии в 8 классе Презентация на тему Приёмы быстрого счета
Презентация на тему Приёмы быстрого счета  Презентация на тему Равнобедренный треугольник, признаки равенства треугольников
Презентация на тему Равнобедренный треугольник, признаки равенства треугольников  Разложение на множители с помощью формул
Разложение на множители с помощью формул Проектная деятельность на уроках математики. Задания для групповой работы (1-2 класс)
Проектная деятельность на уроках математики. Задания для групповой работы (1-2 класс) Неопределённый интеграл
Неопределённый интеграл Задачи на умножение
Задачи на умножение Прятки с фигурами
Прятки с фигурами Построение сечений
Построение сечений Основы матричной алгебры
Основы матричной алгебры Тригонометрические функции, их свойства и графики
Тригонометрические функции, их свойства и графики Деление и степень числа. Тест
Деление и степень числа. Тест Организация работы учителя с обучающимися, испытывающими трудности в обучении математике на уровне основного общего образования
Организация работы учителя с обучающимися, испытывающими трудности в обучении математике на уровне основного общего образования Закономерности между элементами фигуры и тенью при освещении параллельными лучами
Закономерности между элементами фигуры и тенью при освещении параллельными лучами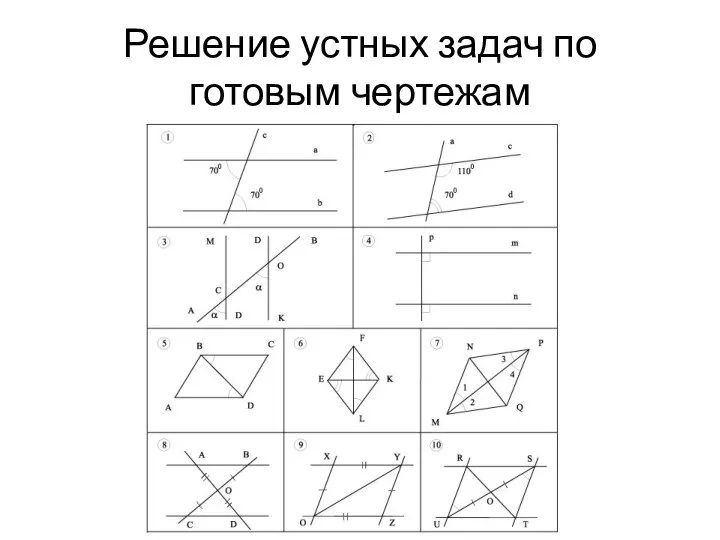 Решение устных задач по готовым чертежам
Решение устных задач по готовым чертежам Элементы высшей математики. Свойства операции умножения
Элементы высшей математики. Свойства операции умножения Окружность и круг
Окружность и круг