Применение производной для нахождения наибольших и наименьших значений величин

Наибольшее и наименьшее значения непрерывной функции на промежутке.
3

Если функция непрерывна на отрезке, то она достигает на нем и наибольшего, и наименьшего значений.

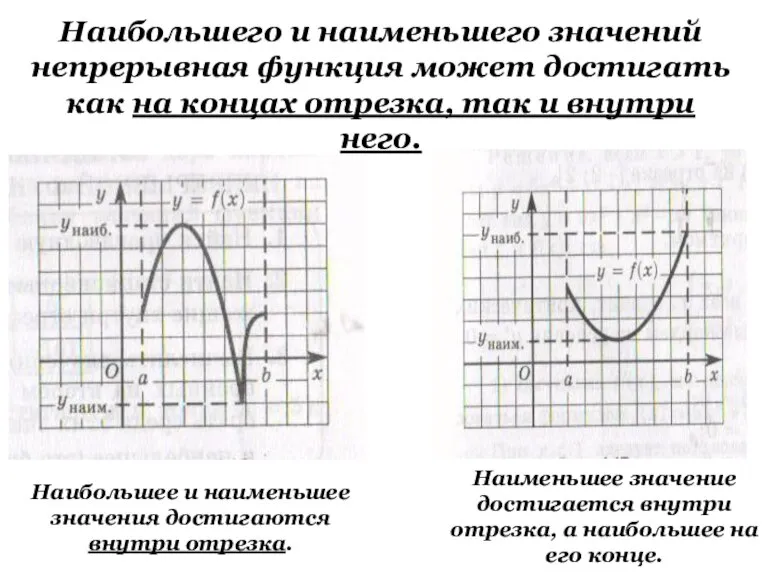
Наибольшего и наименьшего значений непрерывная функция может достигать как на концах отрезка, так и внутри него.
Наибольшее и наименьшее значения достигаются внутри отрезка.
Наименьшее значение достигается внутри отрезка, а наибольшее на его конце.

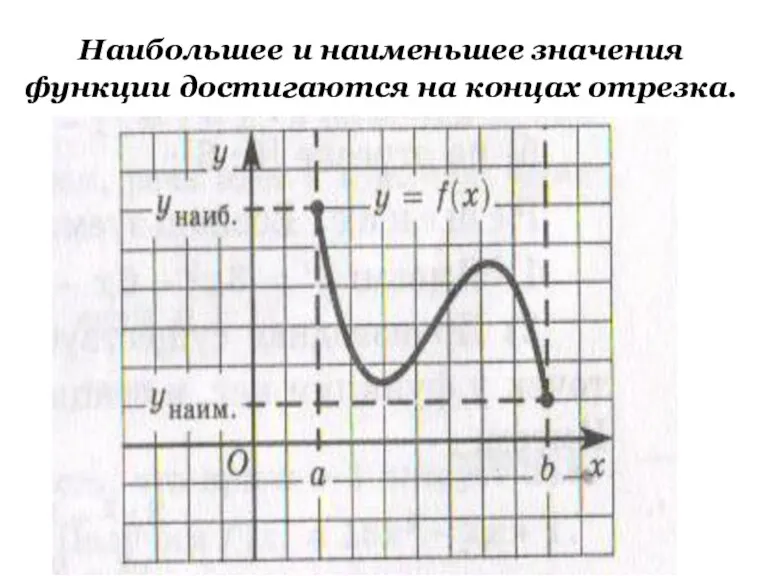
Наибольшее и наименьшее значения функции достигаются на концах отрезка.

Алгоритм нахождения наименьшего и наибольшего значений непрерывной функции y=f(х) на отрезке [а;в].
1. Найти производную функции .
2.Найти точки, в которых производная обращается в 0
3. На числовой прямой отметить отрезок [a;b]и отметить точки, лежащие внутри отрезка [а;в].
4.Вычислить значения функции y=f(х) в точках, отобранных на втором шаге, и в точках а и в .
5. Выбрать среди этих значений наименьшее и наибольшее.

Решение:
2.Решим уравнение .
Пример. Найти наименьшее и наибольшее значения
функции на отрезке [-4;0].