Содержание
- 2. Возведём двучлен во вторую и третью степени: Возведём двучлен в четвёртую и пятую степени алгебраическим способом:
- 3. Теперь нам известны степени одночленов для любой натуральной степени, но коэффициенты остаются неизвестными. Понаблюдаем за коэффициентами
- 4. Нам известны боковые коэффициенты, но неизвестны коэффициенты находящиеся внутри треугольника. Понаблюдав за ними, мы догадались, чтобы
- 6. Скачать презентацию



 Теорема Пифагора
Теорема Пифагора Умножение на двузначные и трёхзначные числа
Умножение на двузначные и трёхзначные числа Определение перемещения
Определение перемещения Связь суммы со слагаемыми
Связь суммы со слагаемыми Теорема Пифагора
Теорема Пифагора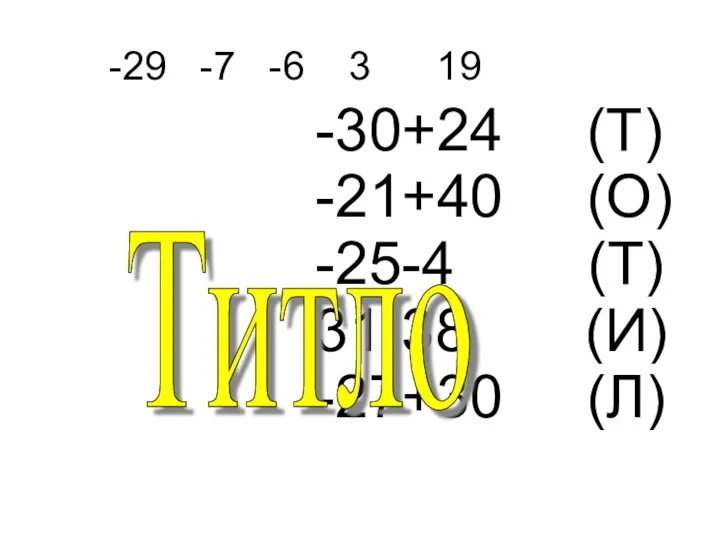 Титло
Титло ЕГЭ. Базовый уровень. Действия с дробями
ЕГЭ. Базовый уровень. Действия с дробями Функции у=|x| и ей график
Функции у=|x| и ей график Sluchaynye_velichiny_14_sen
Sluchaynye_velichiny_14_sen Задачи на части
Задачи на части Направления и лучи
Направления и лучи Площадь. Площадь трапеции
Площадь. Площадь трапеции Прямолинейное неравномерное движение
Прямолинейное неравномерное движение Геометрическая прогрессия в экономике
Геометрическая прогрессия в экономике Классная работа по математике
Классная работа по математике Деление десятичной дроби на натуральное число
Деление десятичной дроби на натуральное число Презентация на тему СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С ОДИНАКОВЫМИ ЗНАМЕНАТЕЛЯМИ
Презентация на тему СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С ОДИНАКОВЫМИ ЗНАМЕНАТЕЛЯМИ  Свойства равнобедренного треугольника
Свойства равнобедренного треугольника Анализ ошибок. Параллелепипеды. 10 класс
Анализ ошибок. Параллелепипеды. 10 класс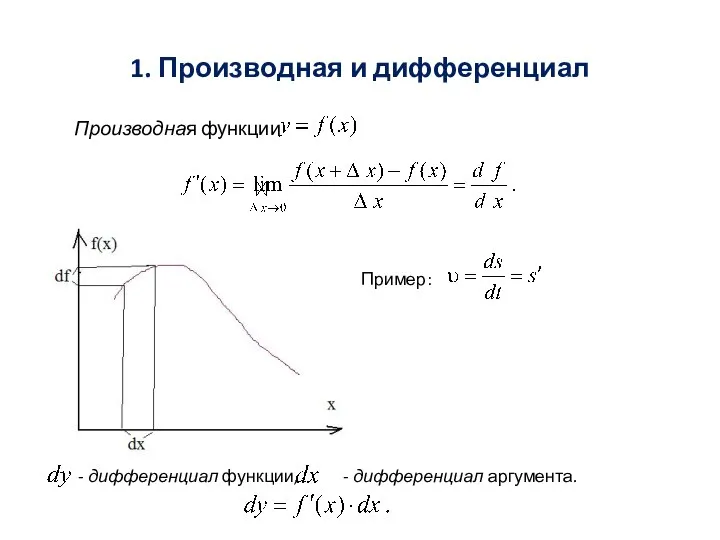 Производная и дифференциал
Производная и дифференциал Степенные, показательные, логарифмические и тригонометрические функции
Степенные, показательные, логарифмические и тригонометрические функции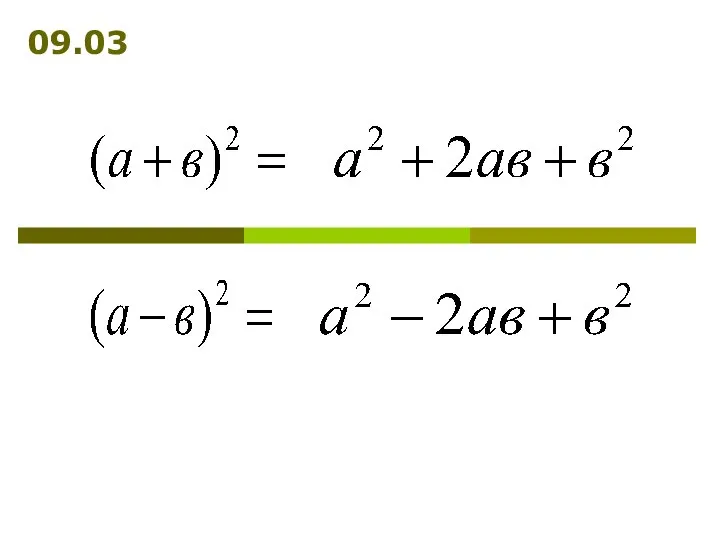 Преобразование многочленов с помощью формул сокращённого умножения
Преобразование многочленов с помощью формул сокращённого умножения Тригонометрические функции, их свойства и графики
Тригонометрические функции, их свойства и графики Многогранники. Виды многогранников
Многогранники. Виды многогранников Сложение с переходом через десяток вида +8, +9. Считаем с гномами
Сложение с переходом через десяток вида +8, +9. Считаем с гномами Окружность. Круг
Окружность. Круг деление многочлена на многочлен столбиком
деление многочлена на многочлен столбиком Соста числа 11
Соста числа 11