Слайд 2Правильные многогранники
В стереометрии особое место занимают геометрические тела с абсолютно равными между

собой гранями, в вершинах которых соединяется одинаковое количество рёбер. Эти тела получили название Платоновы тела, или правильные многогранники. Виды многогранников с такими свойствами насчитывают всего пять фигур:
Тетраэдр ( в основании лежит треугольник) (треугольная пирамида) ( 4 грани)
Гексаэдр (в основании лежит квадрат) ( куб) ( 6 граней)
Октаэдр ( в основании лежит треугольник) ( 8 граней)
Додекаэдр ( в основании пятиугольник) ( 12 граней)
Икосаэдр ( в основании равнобедренный треугольник) (20 граней)
Слайд 3ПРАВИЛЬНЫМ называется многогранник, в основании которого лежит правильный (равносторонний) многоугольник.
икосаэдр
тетраэдр
гексаэдр
октаэдр
додекаэдр

Слайд 4Правильный тетраэдр
Составлен из четырёх равносторонних треугольников. Каждая его вершина является вершиной трёх

треугольников. Сумма плоских углов при каждой вершине равна 180 градусам.
Слайд 5Развертка правильного тетраэдра

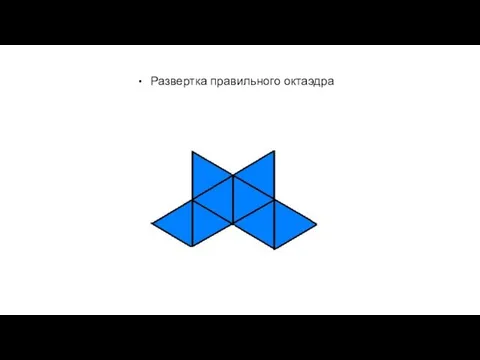
Слайд 6Правильный октаэдр
Составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной равносторонних

треугольников. Сумма плоских углов при каждой вершине равна 240 градусов.
Слайд 7Развертка правильного октаэдра
Слайд 8Правильный икосаэдр
Составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти

треугольникв. Сумма плоских углов при каждой вершине равна 300 градусам.
Слайд 9 Развертка правильного икосаэдра

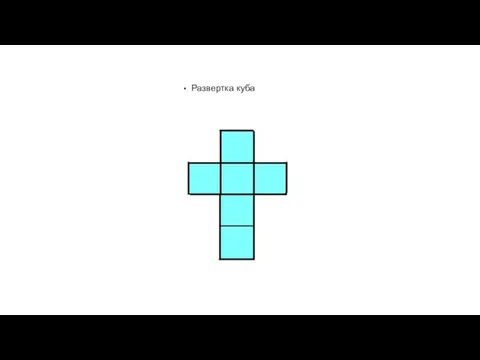
Слайд 10КУБ
Составлен и шести квадратов. Каждая вершина куба является вершиной трёх квадратов. Сумма

плоских углов при каждой вершине равна 270 градусов.
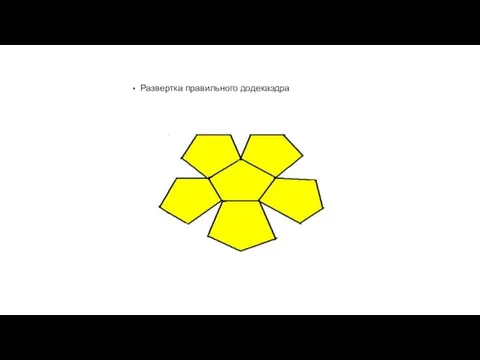
Слайд 12Правильный додекаэдр
Составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трёх

правильных пятиугольников.
Сумма плоских углов при каждой вершине равна 324 градусам.
Слайд 13 Развертка правильного додекаэдра
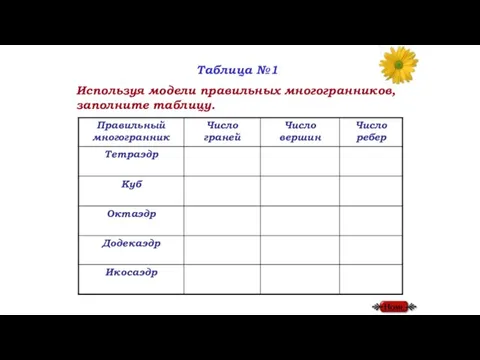
Слайд 16Таблица №1
Используя модели правильных многогранников, заполните таблицу.


















 Презентация на тему ОБЪЁМ ТЕЛ
Презентация на тему ОБЪЁМ ТЕЛ  Задачи на движение в противоположных направлениях
Задачи на движение в противоположных направлениях Решение уравнений: рациональных и иррациональных
Решение уравнений: рациональных и иррациональных Параллельность и перпендикулярность прямых и плоскостей в пространстве
Параллельность и перпендикулярность прямых и плоскостей в пространстве Это страшное слово: Параметр
Это страшное слово: Параметр Математика и живопись
Математика и живопись Презентация на тему ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ В ПРОСТРАНСТВЕ
Презентация на тему ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ В ПРОСТРАНСТВЕ  Тела вращения
Тела вращения Математический кроссворд
Математический кроссворд Графический метод решения уравнений. Задания для устного счета
Графический метод решения уравнений. Задания для устного счета Упрощение выражений. Восстановите цепочку вычислений
Упрощение выражений. Восстановите цепочку вычислений Элементы теории фредгольмовых отображений
Элементы теории фредгольмовых отображений ИСТОРИЯ СИСТЕМ СЧИСЛЕНИЯ
ИСТОРИЯ СИСТЕМ СЧИСЛЕНИЯ Тренажёр. Табличное умножение
Тренажёр. Табличное умножение Прибавление числа 6 с переходом через десяток
Прибавление числа 6 с переходом через десяток Проецирование
Проецирование Тригонометрические функции двойного угла
Тригонометрические функции двойного угла Распределительное свойство умножения
Распределительное свойство умножения Геометрические фигуры
Геометрические фигуры Презентация на тему Сложение и вычитание трехзначных чисел (2 класс)
Презентация на тему Сложение и вычитание трехзначных чисел (2 класс)  Математика, Устный счёт
Математика, Устный счёт Графики и диаграммы
Графики и диаграммы Единицы измерения, масштабы шкал
Единицы измерения, масштабы шкал Некоторые методические приемы для работы с детьми ЗПР на уроках математики
Некоторые методические приемы для работы с детьми ЗПР на уроках математики Числовая последовательность. Предел последовательности; сходящиеся и расходящиеся последовательности
Числовая последовательность. Предел последовательности; сходящиеся и расходящиеся последовательности Расчёт скорости официанта от кассы до столика
Расчёт скорости официанта от кассы до столика Концентрация. Часть II
Концентрация. Часть II Отрицательные числа в географии
Отрицательные числа в географии