Дифференциальные уравнения 1 порядка

Литература
Высшая математика: учебное пособие / В.И. Белоусова, Г.М. Ермакова, М.М. Михалева, Н.В. Чуксина, И.А. Шестакова – Екатеринбург: Изд-во Урал. ун-та, 2017. – Ч.II. – 277 с.
Краснов М. Л., Киселёв А. И., Макаренко Г. И. Сборник задач по обыкновенным дифференциальным уравнениям. Едиториал «УРСС», 2002, – 256 с.
Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. Т.3. М.: Дрофа, 2004. – 512с.
Данко П. Е., Попов А. Г., Кожевникова Т. Я. Высшая математика в упражнениях и задачах. Ч 1. М.: Высшая школа, 1999. – 304 с.

Понтрягин ЛС Обыкновенные ДУ. – М, 1961.
Филлипов АФ Сборник задач по ДУ. – М, 2008.
Сборник задач по математике для ВТУЗов: учеб.лит./ Под ред. Ефимова, Поспелова, Ч.2, 2003.

Дифференциальные уравнения
Любой процесс, в котором есть движение, описывается ДУ
§1. Основная терминология дифференциальных уравнений
Уравнение, связывающее неизвестную функцию, её аргументы, её производные, называется дифференциальным уравнением.
Порядок дифференциального уравнения – порядок старшей производной, входящей в это уравнение.
Пример: y(4) – y + x = 0 - уравнение четвёртого порядка.

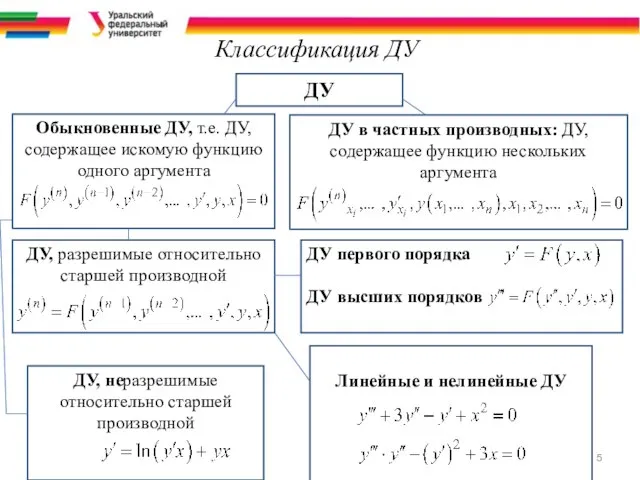
Классификация ДУ
ДУ
ДУ, разрешимые относительно старшей производной
Обыкновенные ДУ, т.е. ДУ, содержащее искомую функцию одного аргумента
ДУ в частных производных: ДУ, содержащее функцию нескольких аргумента
ДУ, неразрешимые относительно старшей производной
ДУ первого порядка
ДУ высших порядков
Линейные и нелинейные ДУ

В данном курсе будут рассматриваться только обыкновенные дифференциальные уравнения, разрешенные относительно старшей производной, т. е. уравнения вида:
y(n)= f(x, y, y', y",…, y(n-1)).
Решение ДУ
Функция y = φ(x), x∈(a, b), непрерывная и n раз дифференцируемая на (a, b), называется решением дифференциально уравнения n-го порядка на (a, b), если при подстановке её в уравнение вместо неизвестной функции и её производных обращает уравнение в тождество на указанном интервале.
График решения дифференциального уравнения называют интегральной кривой.

Основная задача теории ДУ:
решить ДУ, т. е. найти все его решения и описать их свойства.
Процедура отыскания решений ДУ
(чаще всего связанная с интегрированием)
называется интегрированием ДУ.
ДУ считается решённым, если его решение сведено к неопределённому интегралу (к квадратуре).
Универсального метода решения ДУ не существует.

Методы решения ДУ:
Точные (аналитические).
Приближенные
Численные
Графические

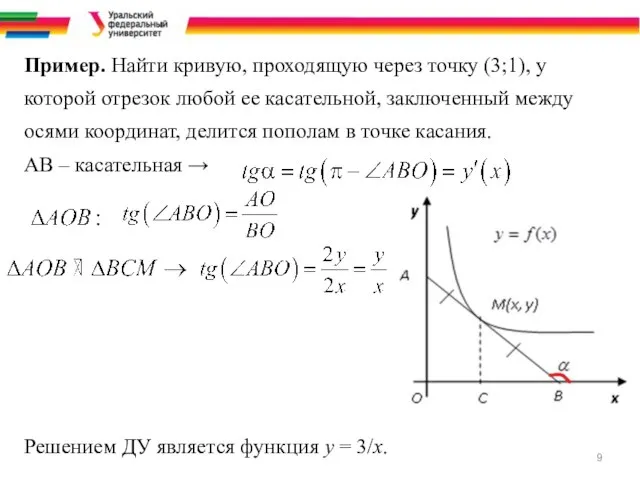
Пример. Найти кривую, проходящую через точку (3;1), у которой отрезок любой ее касательной, заключенный между осями координат, делится пополам в точке касания.
AB – касательная →
Решением ДУ является функция у = 3/х.

§2. Дифференциальные уравнения первого порядка.
Дифференциальное уравнение первого порядка имеет вид: F(x, y, y')=0,
где x − независимая переменная;
y = y(x) − искомая функция;
y' − её производная.
Иногда уравнение можно разрешить относительно y': y' = f(x, y).
Последнее уравнение можно записать в дифференциальной форме, заменив y' на dy/dx:
P(x, y) dx + Q(x, y) dy = 0.

Например, уравнение y' = x2/y можно записать в виде dy/dx = x2/y или x2 dx − y dy = 0.
Дифференциальное уравнение в общем случае имеет бесконечное множество решений.
Например, решением уравнения y' = cos x является функция y = sin x, а также функции
y = sin x+3, y = sin x − 1,5
и ,в общем случае, y = sin x + С , где С − const.

Чтобы получить одно решение дифференциального уравнения, необходимо подчинить его некоторым дополнительным условиям.
Условие, что функция у(х) должна быть равна определенному значению у0, при х0, называется начальным условием.
Начальное условие записывают в виде:
у(х0)= у0 или

Общим решением дифференциального уравнения первого порядка называется функция у = φ(х, С), содержащая одну произвольную постоянную и удовлетворяющая условиям:
а) функция φ(х, С) есть решение дифференциального уравнения при любом конкретном значении постоянной С;
б) каково бы ни было допустимое начальное условие, можно найти такое значение постоянной С=С0, что функция у=φ(х, С0) удовлетворяет данному начальному условию.
Частным решением дифференциального уравнения первого порядка называется любая функция у=φ(х, С0), полученная из общего решения у=φ(х, С) при конкретном значении постоянной С=С0.

С геометрической точки зрения общее решение дифференциального уравнения есть семейство интегральных кривых на плоскости Оху;
частное решение – одна интегральная кривая этого семейства, проходящая через заданную точку.
Задача отыскания частного решения дифференциального уравнения первого порядка , удовлетворяющего данному начальному условию, называется задачей Коши
(Огюстен Луи Коши (1789-1857)- французский математик).

Теорема (существования и единственности решения задачи Коши). Если в уравнении y' = f(x, y) функция f(x, y) и её частная производная f 'y (x, y) непрерывны в некоторой области, содержащей точку (х0, у0), то в этой области существует единственное решение у = φ(х) этого уравнения, удовлетворяющее начальному условию у(х0) = у0.
(без доказательства)
Геометрический смысл теоремы состоит в том, что существует единственная интегральная кривая дифференциального уравнения, проходящая через точку (х0, у0), если выполняется условие теоремы.

В процессе решения дифференциального уравнения нередко приходят к соотношению вида Ф(х, у, С) = 0, которое неявно определяет искомую функцию .
Такое равенство называют общим интегралом дифференциального уравнения, а равенство
Ф(х, у, С0) = 0 называется частным интегралом уравнения.
Решение дифференциального уравнения называется особым, если в каждой его точке нарушается единственность решения задачи Коши.
Особое решение нельзя получить из общего решения дифференциального уравнения ни при каком значении (даже при С = ∞).

Пример: рассмотрим уравнение
– общее решение;
– частное решение;
у≡0 – особое решение ДУ.

Геометрический метод решения. Метод изоклин.
Уравнение y' = f(x, y) в каждой точке (x, y) области D, в которой задана функция f(x, y), определяет - угловой коэффициент касательной к решению, проходящему через точку (x, y), т.е. направление, в котором проходит решение через эту точку.
Говорят, что ДУ задаёт в D поле направлений. График любого решения дифференциального уравнения (интегральная кривая) в любой своей точке касается этого поля, т.е. проходит в направлении, определяемом полем.

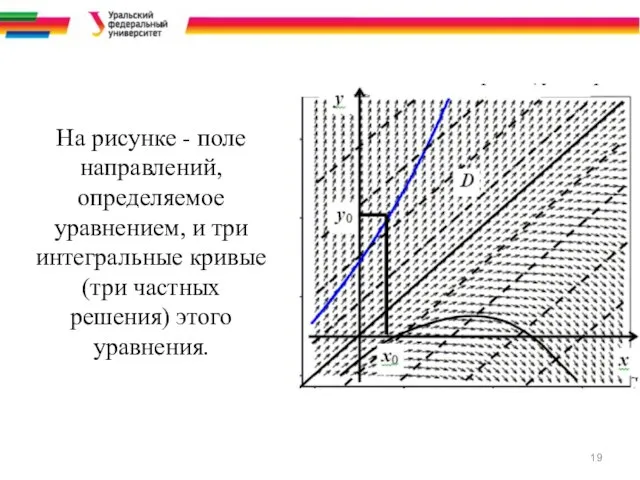
На рисунке - поле направлений, определяемое уравнением, и три интегральные кривые (три частных решения) этого уравнения.

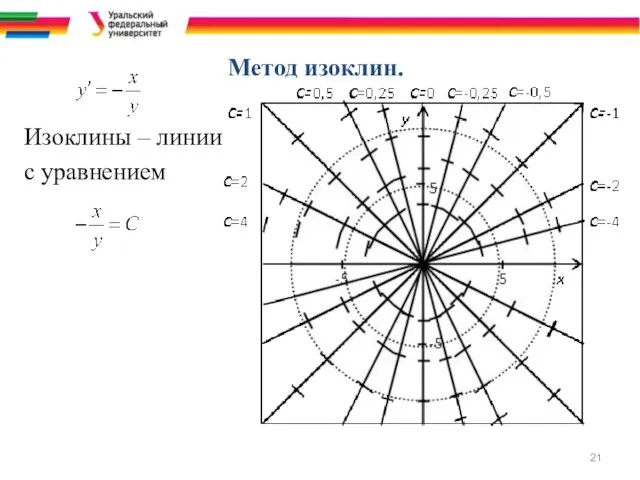
Метод изоклин.
Для изображения поля направлений, задаваемого дифференциальным уравнением, рассматривают линии уровня функции f(x, y), т.е. геометрические места точек, в которых касательные к интегральным кривым сохраняют постоянное направление.
Такие линии называются изоклинами.
С помощью изоклин можно приближённо изобразить интегральные кривые.

Метод изоклин.
Изоклины – линии
с уравнением