Слайд 2 № 302
Дано:
ABCDS- пирамида
О – точка пересечения диагоналей
АB = 3 см
АD
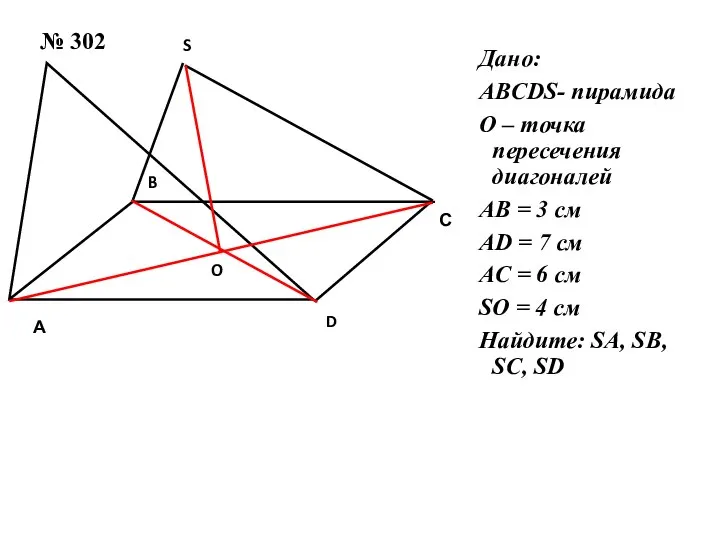
= 7 см
AC = 6 см
SO = 4 см
Найдите: SA, SB, SC, SD
А
С
D
B
S
O
Слайд 3Решение:
1. SABCD пирамида, АВCD -параллелограмм
2.По свойству параллелограмма найдем:
BO = OD и AO

= OC
BO ⊥ пл.ABC, SO = 4 см
∆ OSB = ∆OSD ( по двум катетам), тогда SB = SD;
∆ AOS = ∆ COS ( по двум катетам), тогда SB = SC;
Пусть AO = OC = ½ AC = 3 см, BO = OD = x
Из ∆ ACD по теореме косинусов имеем:
AD2 = AC2 + CD2 -2 AC *CD *cosA
72 = 62 + 32 – 2 *6 * 3 * cosA ,
49 = 36+9-36 * cosA,
36cosA = -4;
cosA= -4/36 = -1/9
Из ∆ COD по теореме косинусов имеем:
X2 = 9+9+2*9*1/9 = 18+2=20, x =2√5 (см)
Из прямоугольного ∆ SOB по теореме Пифагора имеем:
SD = √SO2 + OD2 = √42 +20 = √36 = 6 (cм)
Из прямоугольного ∆ SOC по теореме Пифагора имеем:
SC = √SO2 + OC2 = √42 + 32 = √25 = 5 cм, SC =SA =5 см
Ответ: 5см 5 см 6 см 6см
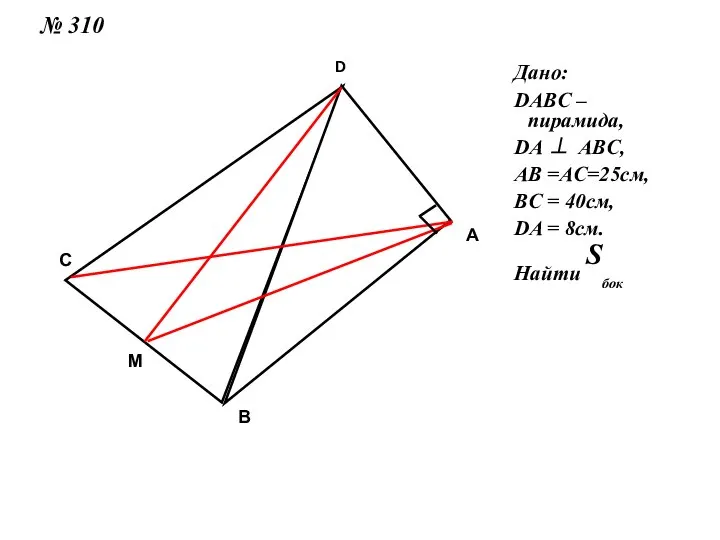
Слайд 4№ 310
Дано:
DABC – пирамида,
DA ⊥ ABC,
AB =AC=25см,
BC = 40см,
DA = 8см.
Найти Sбок
Слайд 5Решение:
1. DABC пирамида, DA⊥(ABC)
2.Sбок =SABD +SADC +SBDC;
Sбок =SADC = DH*AC /2 =

8*25/2=100см2)
Из ∆ABD по т. Пифагора имеем:
BD=√AB2+DA2 = √252+82 = √689 см.
Из ∆ BDM по т. Пифагора имеем:
AB2+DA2 = √252+82 = √689 см
DM2 = BD2 –BM2 = 689 – 400 = 289,
DM = 17
SBDC = (DM*BM)* ½*2 = 17*20=340 см2
Sбок = 100+100+340 = 540см2
Ответ: 540 см2
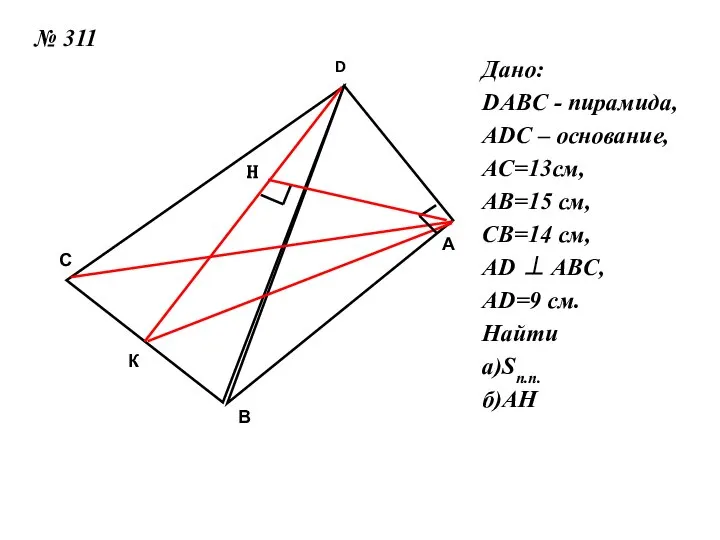
Слайд 6№ 311
D
А
В
С
К
Дано:
DABC - пирамида,
ADC – основание,
AC=13см,
AB=15 см,
CB=14 см,
AD ⊥ ABC,
AD=9
Слайд 7Решение:
1. DABC пирамида, DA⊥(ABC)
2. ∆ DAB и ∆ DAC прямоугольные
SBDA = ½DA

* BA = ½ * 9 * 15 (см2), SCDA= ½ DA * CA = ½ * 9 * 13 (см2).
По формуле Герона имеем:
SABC = √p(p-a) (p-b) (p-c) , где a = 14, b = 15, c = 13, а p = (AB + AC +CB) /2 = (13 + 14 + 15) /2= 21 см
3. Построим АК ⊥ ВС и отрезок DK. По теореме о 3-х перпендикулярах имеем DK⊥ BC.
Проведем в плоскости ADK отрезок AH⊥ DK
AH ⊥ DK – по построению, и AH ⊥ BC, т.к AH принадлежит пл.ADK то пл.ADK ⊥ BC.
AH перпендикулярна двум пересекающимся прямым плоскости BCD, а значит AH ⊥ пл.BCD.






 Презентация на тему Уравнение х2=а (8 класс)
Презентация на тему Уравнение х2=а (8 класс) 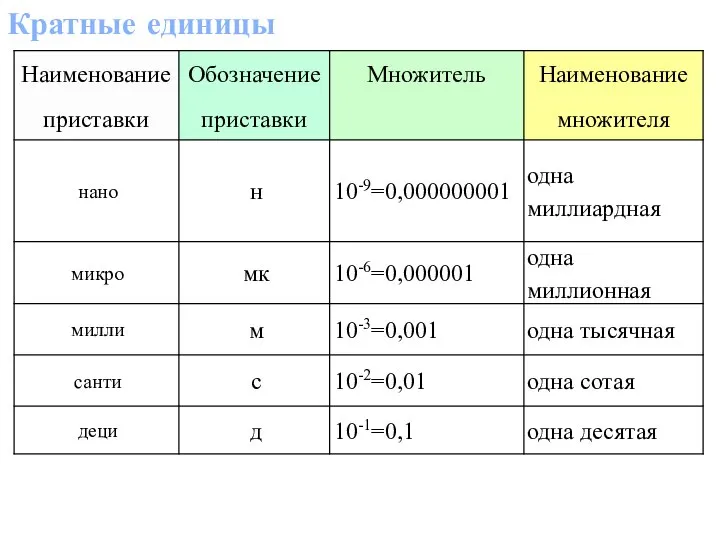 Кратные единицы
Кратные единицы Теорема Пифагора
Теорема Пифагора Линейная функция. Решение задач
Линейная функция. Решение задач Фигуры на клетчатой бумаге
Фигуры на клетчатой бумаге 123
123 Формулы логики
Формулы логики Площадь треугольника
Площадь треугольника Интеграл. Определенный интеграл. Свойства
Интеграл. Определенный интеграл. Свойства Созвездия. Сималтиниус Раунд Тэйбл
Созвездия. Сималтиниус Раунд Тэйбл Векторы в пространстве
Векторы в пространстве Наука Метрология
Наука Метрология Имитационное моделирование
Имитационное моделирование Xüsusi törəməli diferensial tənliklərin həlli metodları
Xüsusi törəməli diferensial tənliklərin həlli metodları Вычисление производной
Вычисление производной Арксинус. Решение уравнения Sin t = a
Арксинус. Решение уравнения Sin t = a Задача на спрос и предложение
Задача на спрос и предложение Перемещение, путь, траектория. 9 класс
Перемещение, путь, траектория. 9 класс Углы треугольника
Углы треугольника Презентация на тему Слагаемые Сумма
Презентация на тему Слагаемые Сумма  Михаил Васильевич Ломоносов. Умножение и деление степеней с натуральными показателями
Михаил Васильевич Ломоносов. Умножение и деление степеней с натуральными показателями Применение производной в географии
Применение производной в географии Деление десятичной дроби на натуральное число
Деление десятичной дроби на натуральное число Презентация на тему Равнобедренный треугольник, признаки равенства треугольников
Презентация на тему Равнобедренный треугольник, признаки равенства треугольников  Иррациональные уравнения. Задания для устного счета
Иррациональные уравнения. Задания для устного счета The determinant of a matrix. Part 3-1
The determinant of a matrix. Part 3-1 Параллельное проектирование
Параллельное проектирование Задачи по геометрии
Задачи по геометрии