Л 8 Предел функции

В1. Предел функции в точке и на бесконечности
Рассмотрим функцию у=f(x), определенную на множестве Х и точку х0, быть может, и не принадлежащую множеству Х, но обладающей тем свойством, что в любой её окрестности есть точки множества Х.

Определение 1. (по Гейне)
Число А называется пределом функции y=f(x) в точке х0, если для любой последовательности {xn} сходящейся к х0 соответствующая последовательность значений функции { f(xn) } сходится к числу А.

Определение 2. (по Коши)
Число А называется пределом функции f(x) в точке х0, если для каждого ε > 0 можно указать такое число δ > 0, что для всех хϵX и х≠х0 и удовлетворяющих неравенству |x–х0|<δ, имеет место неравенство |f(x)–A|<ε.
Обозначение или
f(x)→А при х→х0

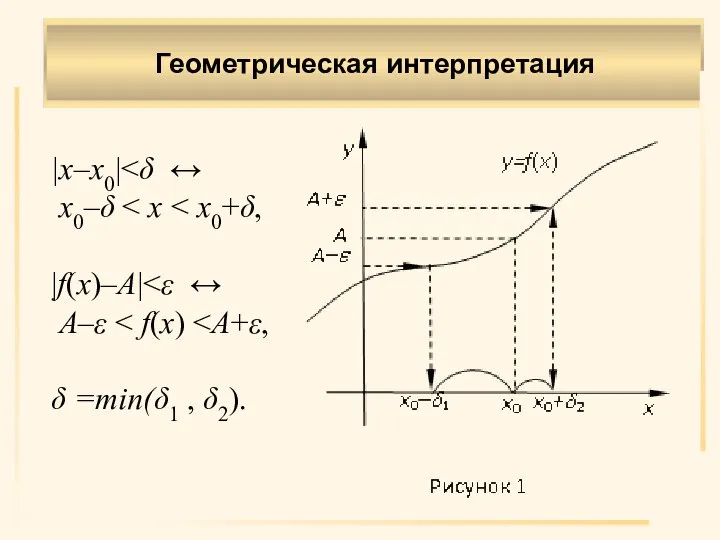
Геометрическая интерпретация
|x–х0|<δ ↔
х0–δ < х < х0+δ,
|f(x)–A|<ε ↔
А–ε < f(x) <А+ε,
δ =min(δ1 , δ2).

Предположим, что f(x) определена при сколь угодно больших значениях x, то есть Х= D(f ) неограниченна.
Определение 3. (по Гейне). Число А называется пределом функции f(x) на бесконечности, то есть при если , соответствующая последовательность
Обозначают:

Определение 4. (по Коши)
Число А называется пределом функции f(x) на бесконечности, то есть при
если такое, что
выполняется условие

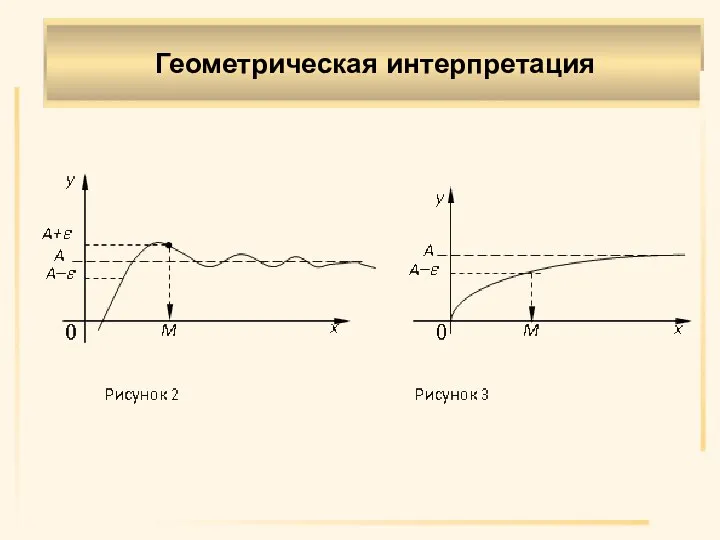
Геометрическая интерпретация

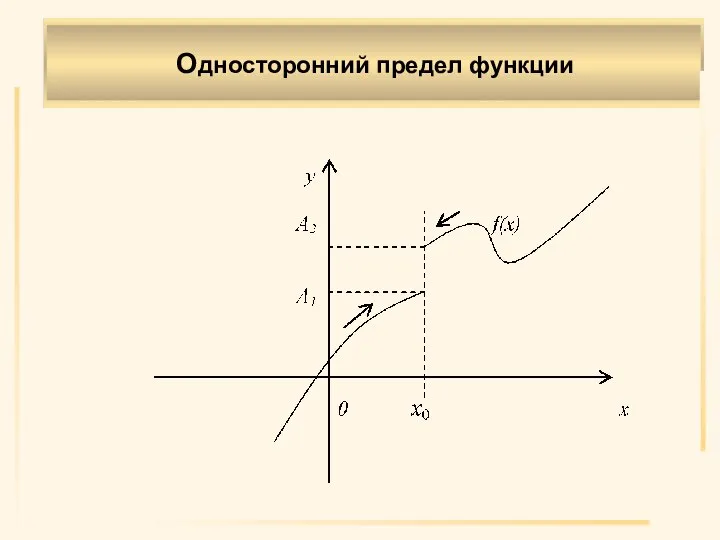
Односторонние пределы
Определение 5. Если f(x) → A1 при х→х0 только при x < х0, то
- называется пределом функции f(x) в точке х = х0 слева,
а если f(x) → A2 при х → х0 только при
x > х0, то
называется пределом функции f(x) в точке х = х0 справа.

Определение 6.
Число A1 (A2) называется правым (левым) пределом функции f(x) в точке х0, если ∀ε>0, ∃δ>0 такое, что ∀х∈Х и удовлетворяющих условиям |x–х0|<δ и х>x0 (x

Обозначения односторонних пределов
Обозначение предела справа
f(x0+0) или
Обозначение предела слева
f(x0–0) или

Односторонний предел функции

Свойство 1. (Единственность предела). Если и то А=В.
Свойство 2. Если существует то f(х) ограничена в некоторой окрестности х0.
2. Основные свойства предела функции

Если f(x) монотонна и ограничена в некоторой окрестности точки
х = х0 , то существует
Свойство 3.

Если функции f(x) и g(x) имеют в точке х0 конечные пределы А и В, то
Свойство 4.

Если в окрестности точки х0, (исключая быть может саму точку х0), выполняется условие f(x)≤ ϕ(x) ≤g(x) и
то функция ϕ(x) также имеет предел в точке х0 и
Свойство 5.

Если в окрестности точки х0, (исключая быть может саму точку х0), выполняется условие f(x) ≤ g(x) и
то А ≤ В.
Свойство 6.

Определение 7. Функция f(x) называется бесконечно малой в точке x0, если
Обозначают α(х), β(х).
3. Бесконечно малые функции и их свойства

Если где α(х) и β(х)
– бесконечно малые величины при х→а, то функция α(х) называется бесконечно малой более высокого порядка, чем функция β(х).
Определение 8.

Если
то α(х) и β(х) называются бесконечно малыми одного порядка.
Определение 9.

Если то функции α(х) и
β(х) называются эквивалентными бесконечно малыми.
Записывают α(х) ~ β(х).
Пример. Сравнить бесконечно малые функции f(x)=x10 и f(x)=x при х→0.
Определение 10.

Бесконечно малая функция α(х) называется бесконечно малой порядка k относительно бесконечно малой функции β(х), если предел
конечен и отличен от нуля.
Определение 11.

Свойство 1. Сумма конечного числа бесконечно малых функций при х→х0 тоже бесконечно малая функция при х→х0.
Свойства бесконечно малых функций

числа бесконечно малых функций при х→х0 тоже бесконечно малая функция при х→х0.
Свойство 3. Произведение бесконечно малой функции на функцию, ограниченную в окрестности точки х=х0 является бесконечно малой функцией при х→х0.
Свойство 2. Произведение конечного

Частное от деления бесконечно малой функции на функцию, предел которой не равен нулю, есть величина бесконечно малая.
Свойство 4.

Для того, чтобы
необходимо и достаточно выполнение условия f(x)–A=α(x), где α(x) – бесконечно малая функция.
Свойство 5.

Если α(х)~β(х) и β(х)~γ(х), то α(х)~γ(х) .
Свойство 6.

Если α(х)~α1(х) и β(х)~β1(х) и
то
или
Свойство 7.