Дифференциальные уравнения

При решении различных задач математики, физики и других наук часто пользуются математическими моделями в виде уравнений, связывающих независимую переменную x , искомую функцию
y = f(x) и ее производные
Основные понятия
Такие уравнения называются дифференциальными уравнением (ДУ) (термин принадлежит Лейбницу, 1676)
Символически дифференциальное уравнение можно написать:
Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение.
Например, уравнение
есть уравнение второго порядка.

Основные понятия
Если искомая функция y = f(x) есть функция одной независимой переменной, то дифференциальное уравнение называется обыкновенным, в противном случае – ДУ в частных производных.
Решением дифференциального уравнения называется функция, которая при подстановке в уравнение обращает его в тождество, процесс отыскания решения называется интегрированием ДУ
Например, рассмотрим уравнение:
Функция
является решением уравнения, так как:
При подстановке функции и ее производных в уравнение получим тождество:

Дифференциальные уравнения первого порядка
Дифференциальное уравнение первого порядка имеет вид:
Если уравнение можно записать в виде:
то его называют ДУ первого порядка, разрешенным относительно производной.
Уравнение первого порядка может быть записано также в дифференциальном виде:
P(x; y) и Q(x; y) – известные функции.
Интегрирование ДУ в общем случае приводит к бесконечному множеству решений, отличающихся друг от друга постоянными величинами.

Дифференциальные уравнения первого порядка
Например, решением уравнения
является функция
и вообще любая функция вида
Чтобы решение дифференциального уравнения приобрело конкретный смысл, его надо подчинить дополнительным условиям.
Условие, что при x = x0 функция у должна быть равна заданному числу у0, называют начальным условием и записывают в виде:
, а также функция

Дифференциальные уравнения первого порядка
Общим решением ДУ первого порядка называется функция
Функция
Каково бы ни было начальное условие у(x0 ) = у0 можно найти такое значение постоянной С0, что функция
содержащая одну произвольную постоянную и удовлетворяющая условиям:
является решением ДУ при каждом
фиксированном значении C.
удовлетворяет данному начальному условию.
Частным решением ДУ первого порядка называется функция, полученная из общего решения при конкретном значении постоянной С = С0 .
Если общее решение ДУ найдено в неявном виде: Ф(x; y; C) = 0, то такое решение называется общим интегралом, уравнение Ф(x; y; С0) = 0 называется частным интегралом.

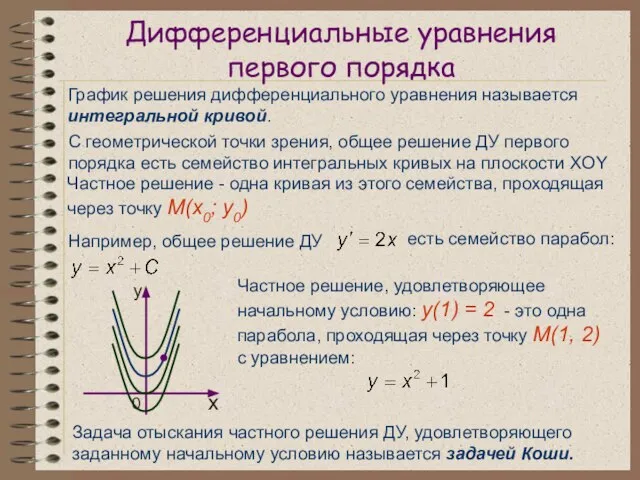
Дифференциальные уравнения первого порядка
График решения дифференциального уравнения называется интегральной кривой.
С геометрической точки зрения, общее решение ДУ первого порядка есть семейство интегральных кривых на плоскости XOY
Например, общее решение ДУ
есть семейство парабол:
Частное решение - одна кривая из этого семейства, проходящая через точку М(х0; у0)
Частное решение, удовлетворяющее начальному условию: у(1) = 2 - это одна парабола, проходящая через точку М(1, 2) с уравнением:
Задача отыскания частного решения ДУ, удовлетворяющего заданному начальному условию называется задачей Коши.

Уравнения с разделяющимися переменными
Наиболее простым ДУ первого порядка является уравнение вида:
Такое уравнение называется уравнением с разделенными переменными.
Проинтегрировав это уравнение почленно, получим:
- общий интеграл ДУ.
Более общий случай описывают уравнения с разделяющимися переменными, которые имеют вид:
(1)
(2)
Уравнение (2) сводится к уравнению (1) путем почленного деления его на

Уравнения с разделяющимися переменными
Получаем:
Замечание: при проведении почленного деления ДУ на
могут быть потеряны некоторые решения.
Поэтому следует отдельно решить уравнение
(3)
Уравнение
и установить те решения, которые не могут быть получены из общего решения – особые решения.
также сводится к уравнению с разделенными переменными.
Для этого достаточно положить

Уравнения с разделяющимися переменными
Разделим обе части уравнения на xy:
Общий интеграл ДУ
Решим уравнение xy = 0:
Его решения: x = 0 и y = 0 являются решениями данного ДУ, но не входят в общее решение, значит это особое решение.
Решить задачу Коши:
Общее решение ДУ
Подставим начальные условия:
Частное решение ДУ

Уравнения с разделяющимися переменными
Рассмотрим задачу, приводящую к ДУ первого порядка с разделяющимися переменными:
Задача: материальная точка массы m замедляет свое движение под воздействием силы сопротивления среды, пропорциональной квадрату скорости V. Найти зависимость скорости от времени. Найти скорость точки через 3 с после начала замедления, если V(0) = 100 м/с, V(1) = 50 м/с.
Решение:
Примем за переменную время t, отсчитываемое от начала замедления точки. Тогда скорость V будет функцией t: V = V(t).
Воспользуемся вторым законом Ньютона:
В нашем случае
- коэффициент пропорциональности