Diskretnaya_matematika-2 2

Учебные пособия
по курсу
«Дискретная математика»:

П.С. Довгий,
В.И. Поляков,
В.И. Скорубский
Основы теории множеств
и приложение булевой алгебры к синтезу комбинационных схем
Учебное пособие по дисциплине
«Дискретная математика»
Санкт-Петербург
2013

П.С. Довгий, В.И. Поляков
СИНТЕЗ КОМБИНАЦИОННЫХ СХЕМ
Учебное пособие к курсовой работе
по дисциплине "Дискретная математика"
Санкт- Петербург
2009

Разделы курса
«Дискретная математика»:
Теория множеств - тест;
Булева алгебра - тест;
Синтез комбинационных схем – тест, КР;
Арифметические основы ЭВМ - тест, ДЗ;
ЗАЧЕТ

Основные понятия теории множеств
Отцом теории множеств считается Георг Кантор.
Георг Кантор (1845 -1918)
Ему принадлежит заслуга привнесения в математику самого понятия "множества" (или "совокупности").

Г. Кантору принадлежит следующая формулировка понятия множества: «Множество — это объединение определённых, различных объектов, называемых элементами множества, в единое целое».

В основе теории множеств лежат первичные понятия:
множество и отношение
«быть элементом множества».
Под множеством будем понимать любую совокупность определенных и различимых между собой объектов, рассматриваемую как единое целое.

Объекты, образующие некоторое множество, называются его элементами. Принадлежность некоторого элемента x множеству A обозначается как
x∈A — «x есть элемент множества A»
или «x принадлежит множеству A» .
Непринадлежность некоторого элемента а множеству М обозначается: а ∉ М.
Множества принято обозначать заглавными буквами латинского алфавита, а элементы множеств – строчными буквами.

Среди производных понятий теории множеств наиболее важны следующие:
Пустое множество. Пустым множеством называется множество, не содержащее ни одного элемента. Пустое множество обозначают символом ∅.
Подмножество и надмножество. Множество A
называется подмножеством множества B, если любой элемент, принадлежащий A, также принадле-жит B. Это записывается в виде отношения включе-ния: A ⊆ B. Таким образом, (A⊆B) ⇔ (x∈A → x∈B). Множество B, в свою очередь, называется надмножеством множества A, что записывается в виде отношения обратного включения: B ⊇ A.

Пустое множество является подмножеством любого множества.
Универсальное множество. Обычно, в конкретных рассуждениях элементы всех множеств берутся из некоторого одного, достаточно широкого множества, своего для каждого случая, которое называется универ-сальным множеством (универсумом).
Универсальное множество обычно обозна-чается U (от англ. universe, universal set),
реже E.

Мощность множества можно рассматривать как числовую характеристику (метрику) любого множества. Мощностью некоторого конечного множества А является число его элементов. Мощность множества А принято обозначать |А|, например, мощность множества А={a, b, c} равна |А|=3.
Мощность пустого множества равна нулю: |∅|=0.

Конечные и бесконечные множества. Множества, имеющие конечное число эле-ментов и, соответственно, конечное значе-ние мощности, называются конечными, а множества с бесконечным числом элементов и, соответственно, с бесконечной мощностью – бесконечными.
Множества, обладающие одинаковым значе-нием мощности, называются равномощными. Понятие равномощности распространяется и на бесконечные множества.

Счетные и несчетные множества. Бесконечные множества разделяются на счётные и несчетные. Бесконечное множество называется счетным, если его элементы можно пронумеровать, в противном случае, бесконечное множество называется несчетным. Простейшим примером счетного множества является множество всех натуральных чисел, в связи с чем можно дать другое определение счетного множества: множество называется счетным, если оно равномощно множеству натуральных чисел, т.е. его можно представить в виде {x0, x1, x2, …}, где хi – элемент множества, однозначно соответствующий его номеру i.

В свою очередь, простейшим примером несчетного множества является множество действительных чисел.
Другими примерами счетных множеств являются множества целых и рациональных чисел, а примером несчетного множества – множество комплексных чисел.
В отношении счетных множеств имеют место следующие теоремы:
- любое подмножество счетного множества является либо конечным, либо счетным, иначе говоря, каждое бесконечное подмножество счетного множества также является счетным;
- объединение конечного числа счетных множеств также является счетным множеством.

Булеан множества. Любое конечное множество содержит и конечное число подмножеств. Связь между произвольным множеством и всеми его подмножествами определяется булеаном.
Булеаном множества А называется множество всех его подмножеств.
Булеан множества А будем обозначать В(А).
Иначе булеан множества А называют множеством - степенью множества А.

Булеан, как множество всех подмножеств множества А, должен включать в себя:
пустое множество;
само множество А;
отдельные элементы множества А;
всевозможные комбинации различных элемен-тов множества А.
Если множество А содержит n элементов, то число его подмножеств из k элементов представляет собой число сочетаний из n по k и определяется по формуле:

Пример. Записать булеан (множество – степень) для множества А={a, b, c}.
B(A)={∅, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}}.
Утверждение. Если множество А состоит из n элементов, то множество B(A) всех его подмножеств состоит из 2n элементов, т.е.
|А|= n → |B(A)|= 2n = 2|А|.

Способы задания множеств
1. Задание множеств списком предполагает перечисление элементов. Например, множество А состоит из букв a, b, c, d : A={a, b, c, d} или множество L включает цифры 0, 2, 3, 4: L={0, 2, 3, 4}.
2. Задание множеств порождающей процедурой означает описание характеристических свойств элементов множества: X = { x | H (x) }, т. е. множество X содержит такие элементы x, которые обладают свойством H (x).
Например: B = { b | b = π / 2 ± k π, k ∈ N },
N - множество всех натуральных чисел.

3. Задание множества описанием свойств элементов. Например, M - это множество чисел, являющихся степенями двойки.
К описанию свойств естественно предъявить требования точности и недвусмысленности.
Так, "множество всех хороших песен 2022 года" каждый составит по-разному. Надежным способом однозначного задания множества является использование разрешающей процедуры, которая для любого объекта устанавливает, обладает ли он данным свойством и соответственно является ли элементом рассматриваемого множества.

Например: S - множество успевающих студентов. Разрешающей процедурой включения во множес-тво S является отсутствие неудовлетворительных оценок в последней сессии.
4. Графическое задание множеств осуществляют с помощью диаграмм Эйлера-Венна. Построение диаграммы заключается в изображении большого прямоугольника, представляющего универсальное множество U, а внутри его – кругов, представля-ющих рассматриваемые множества.

Фигуры должны пересекаться в наиболее общем случае, требуемом в задаче, и должны быть соответствующим образом обозначены.
Точки, лежащие внутри различных областей диаграммы, могут рассматриваться как элементы соответствующих множеств. Имея построенную диаграмму, можно заштриховать определенные области для обозначения вновь образованных множеств.

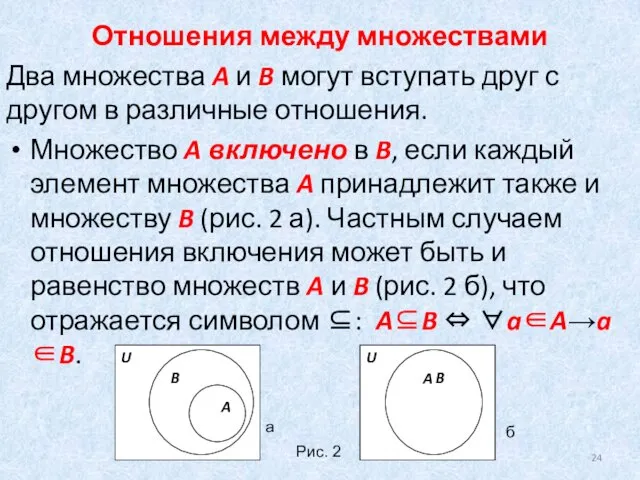
Отношения между множествами
Два множества A и B могут вступать друг с другом в различные отношения.
Множество A включено в B, если каждый элемент множества A принадлежит также и множеству B (рис. 2 а). Частным случаем отношения включения может быть и равенство множеств A и B (рис. 2 б), что отражается символом ⊆: A⊆B ⇔ ∀a∈A→a ∈B.
а
б
Рис. 2

Подобное отношение можно называть нестрогим включением. Довольно часто требуется исключить равенство множеств из отношения включения, в связи с чем, вводится отношение строгого включения.
Множество A строго включено в B, если A включено в B, но не равно ему (рис. 2а), что отражается символом ⊂: A⊂B ⇔ (A⊆B) и (A≠B).
В этом случае множество А называют собственным (строгим, истинным) подмно-жеством множества В.
Примерами использования строгого включения могут являться: A⊂U, B⊂U, ∅⊂А, ∅⊂B.

Отношения между множествами могут обладать следующими свойствами: рефлексивностью, симметричностью и транзитивностью.
Свойство рефлексивности является унарным, т.е. применительно к единственному объекту (в данном случае к множеству) и означает, что отношение применимо к «себе самому».
Простым примером рефлексивного отношения для чисел могут служить отношения «≥» или «≤», т.к. для любого числа d можно записать d ≥ d или
d ≤ d. В свою очередь отношения «>» и «<» этим свойством не обладают, в связи с чем, они называются антирефлексивными.

Свойство симметричности является бинарным (двухместным), т.е. применимо к двум объектам. Отношение является симметричным, если оно выполняется в обе стороны по отношению к паре объектов (в данном случае множеств). Примерами свойства симметричности являются различные геометрические объекты, для которых понятие «симметрии» является наиболее наглядным. Например, отношение: «быть симметричными относительно оси х» в отношении точек плоскости является симметричным. Действительно, если первая точка симметрична второй, то вторая точка обязательно симметрична первой.

В свою очередь, отношение между двумя объек-тами не обладает свойством симметричности, т.е. является антисимметричным, если его выполне-ние в обе стороны имеет место только в случае равенства объектов.
Если записать бинарное отношение между объектами a и b в общем виде aRb, где R – символ отношения, то для симметричного отношения:
aRb → bRa при любых a и b, а для антисимметрич-ного aRb → bRa, только, если a = b.
Примером антисимметричного отношения могут служить отношения «≥» или «≤» между числами. Действительно, (a ≤ b)→(b ≤ a), только, если a = b.

Свойство транзитивности является тернарным, т.е. применяется к трем объектам. Отношение R между объектами a, b, с является транзитивным, если из aRb и bRс следует aRс, т.е. из выполне-ния отношения R между парами объектов (a, b) и (b, с) следует его выполнение и для пары (a, с).
Примерами транзитивного отношения для чисел являются отношения «>», «≥», «<», «≤». Отноше-ние, не обладающее свойством транзитивности, называется нетранзитивным.
Примером нетранзитивного отношения может слу-жить отношение «пересекаться». Действительно для множеств: A={a, b}, B={b, c}, C={c, d} A пересе-кается с B, B - с C, но A не пересекается с C.

Отношение нестрогого включения обладает свойствами:
рефлексивности: А ⊆ А;
антисимметричности: (A ⊆ В и B ⊆ A) → (A=B);
транзитивности: (A ⊆ В и B ⊆ C) → (A ⊆ C).
Отношение строгого включения обладает свойствами:
антирефлексивности: А ⊄ А;
транзитивности : (A ⊂ В и B ⊂ C) → (A ⊂ C).
Свойства симметричности или несимметричности для отношения строгого включения не рассматри-ваются, так как их рассмотрение предполагает случай равенства между объектами отношения.

Для комбинации отношений строгого и нестрогого включений:
(A ⊆ В и B ⊂ C) → (A ⊂ C);
(A ⊂ В и B ⊆ C) → (A ⊂ C).
Множество A равно множеству B, если A и B включены друг в друга или, иначе, между ними существует отношение взаимного включения: A=B ⇔ (A⊆B) и (B⊆A).
Вторая часть равенства указывает на наиболее ти-пичный метод доказательства равенства множеств A и B, который заключается в доказательстве сначала утверждения А⊆В, а затем В⊆А.

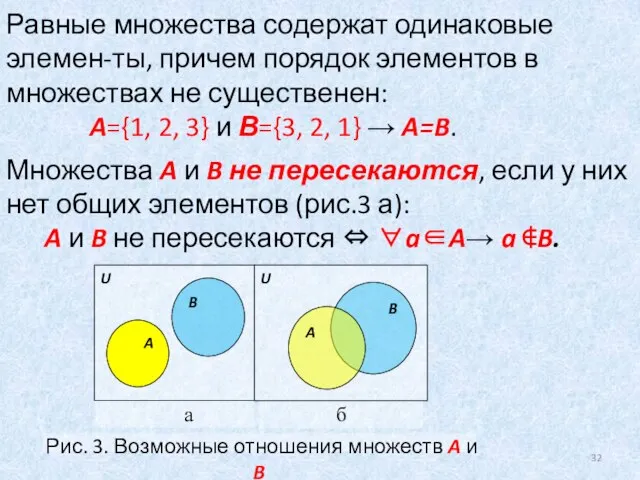
Равные множества содержат одинаковые элемен-ты, причем порядок элементов в множествах не существенен: A={1, 2, 3} и В={3, 2, 1} → A=B.
Множества A и B не пересекаются, если у них нет общих элементов (рис.3 а):
A и B не пересекаются ⇔ ∀a∈A→ a ∉B.

Множества A и B находятся в общем положении, если существуют элемент, принадлежащий исклю-чительно множеству A, элемент, принадлежащий исключительно множеству B, а также элемент, принадлежащий обоим множествам (рис. 3 б):
A и B находятся в общем положении ⇔
∃a, b, c:
[(a∈A) и (a ∉B)] и
[(b ∈B) и (b ∉A)] и
[(c ∈A) и (c ∈B)].

Рассмотрим отношения между числовыми мно-жествами, для которых будем использовать следующие обозначения:
S – множество простых чисел;
N – множество натуральных чисел (т. е. N = {1, 2, 3, … });
Z – множество целых чисел;
Z+ – множество целых неотрицательных чисел (иногда обозначается N0 (т. е. N0 = {0, 1, 2, 3, … }));
Z– – множество целых неположительных чисел;
R – множество действительных чисел;
R+ – множество неотрицательных действительных чисел;

R– – множество неположительных действительных чисел;
V – множество рациональных чисел;
W – множество иррациональных чисел;
К – множество комплексных чисел.
Для этих множеств очевидными являются следующие цепочки отношений включения:
S ⊂ N ⊂ Z+ ⊂ Z ⊂ V ⊂ R ⊂ К;
W ⊂ R ⊂ К.

Алгебра множеств
Множество всех подмножеств универсального множества U вместе с операциями над множест-вами образуют так называемую алгебру подмно-жеств множества U или алгебру множеств.
Основными составляющими алгебры множеств являются операции над множествами и свойства этих операций, которые формулируются в виде основных тождеств или законов алгебры множеств.

Операции над множествами
Над множествами определены следующие операции: объединение, пересечение, разность (относительное дополнение), симметрическая разность и дополнение (абсолютное).
Рис. 4. Объединение множеств
Объединением множеств А и В называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств А, В (рис. 4): A∪B = {x | x∈ A или x∈B}.

Операцию объединения можно распространить на произвольное, в том числе и бесконечное количество множеств, например, М=А∪В∪С∪D.
В общем случае используется обозначение , которое читается так: “объединение всех множеств А, принадлежащих совокупности S ”.
Если же все множества совокупности индекси-рованы (пронумерованы с помощью индексов), то используются другие варианты обозначений:
1. , если S = {A1, A2, …, Ak};

2. , если S – бесконечная совокупность
пронумерованных множеств;
3. , если набор индексов множеств задан ...............множеством I.
Пример 1.
А={a,b,c}, B={b,c,d}, C={c,d,e}.
A∪B={a,b,c,d}; A∪C={a,b,c,d,e}; B∪C={b,c,d,e}; A∪B∪C={a,b,c,d,e}.
Пересечением множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат одновременно как множеству А, так и множеству В (рис. 5):
A∩B = {x | x∈ A и x∈B}.

Рис. 5. Пересечение множеств
Аналогично определяется пересечение произ-вольной (в том числе бесконечной) совокупности множеств. Обозначение для пересечения системы множеств аналогичны рассмотренным ранее обозначениям для объединения.
Пример 2. (для множеств из примера 1):
А∩В = {b, c}; A∩C = {c}; B∩C = {c, d}; A∩B∩C = {c}.

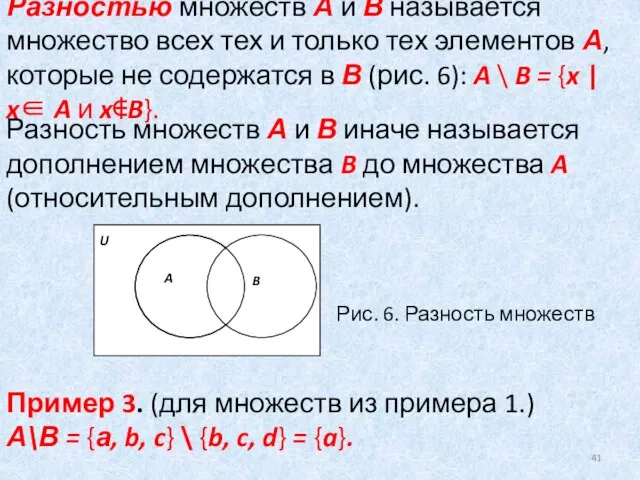
Разностью множеств А и В называется множество всех тех и только тех элементов А, которые не содержатся в В (рис. 6): A \ B = {x | x∈ A и x∉B}.
Рис. 6. Разность множеств
Пример 3. (для множеств из примера 1.)
А\В = {а, b, c} \ {b, c, d} = {a}.
Разность множеств А и В иначе называется дополнением множества B до множества A (относительным дополнением).

Симметрической разностью множеств А и В называется множество, состоящее из элементов, которые принадлежат либо только множеству А, либо только множеству В (рис. 7). Симметрическую разность обозначают как AΔB, A – B или A ⊕ B:
AΔB = {x | (x∈ A и x∉B) или ( x∈ В и x∉А)}.
Рис. 7. Симметрическая разность множеств
Таким образом, симметрическая разность множеств A и B представляет собой объединение разностей (относительных дополнений) этих множеств: AΔB = (A \ B) ∪ (B \ A).

Пример 4. (для множеств из примера 1.)
AΔB ={a}∪{d}={a,d}.
Дополнением (абсолютным) множества А называется множество всех тех элементов х универсального множества U, которые не принадлежат множеству А (рис. 8). Дополнение множества А обозначается: = {x ⎜x∉A} = U \ A.
С учетом введенной операции дополнения, разность множеств А и В можно представить в виде: A \ B = A∩ .
Рис. 8. Дополнение множества

Операции над множествами используются для получения новых множеств из уже существующих. Порядок выполнения операций над множествами определяется их приоритетами в следующем порядке: , ∩ , ∪, \ , Δ.
3. Дистрибутивные (распределительные) законы:
A ∪ (B∩C) = (A∪B) ∩ (A∪C);
A ∩ (B∪C) = (A∩B) ∪ (A∩C).
Основные тождества (законы) алгебры множеств
1.Коммутативные (переместительные) законы:
A∪B = B∪A; A∩B = B∩A.
2. Ассоциативные (сочетательные) законы:
A ∪ (B∪C) = (A∪B) ∪ C; A ∩ (B∩C) =(A∩B) ∩ C.

∅.
4. Законы тавтологии (идемпотентности):
A∪A= A; A∩A= A.
5. Законы двойственности (де Моргана):
Следствия из законов двойственности:
6. Законы поглощения: А∪ (А∩В)=А; А∩(А∪В)=А.
7. Закон инволютивности:
8. Закон противоречия:
9. Закон «третьего не дано»:
10. Свойства универсального множества: А∪U=U; А∩U=А.
11. Свойства пустого множества: А∪∅=А; А∩∅=∅.

15. Дополнительные тождества для операции симметрической разности:
AΔ(BΔC) = (AΔB) ΔC; A∩(BΔC) = (A∩B) Δ(A∩C).
Дополнительные тождества для операций объединения, пересечения и дополнения:
12. Законы склеивания:
13. Законы сокращения (законы Порецкого):
14. Дополнительные тождества для операции разности множеств:
A \ (B \ C)=(A \ B) ∪ (A∩C); (A \ B) \ C=(A \ C) \ (B \ C);
A \ (B∪C)=(A \ B) \ C; A \ (B∪C)=(A \ C) \ (B \ C).

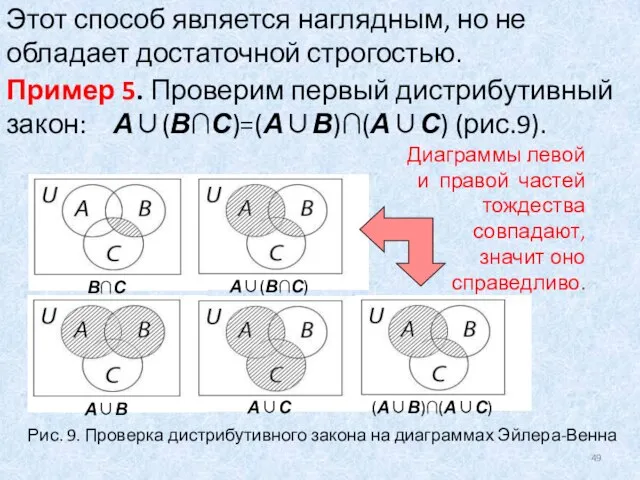
Способы доказательства тождеств
Убедиться в справедливости тождеств можно с помощью диаграмм Эйлера-Венна. Для этого необходимо изобразить на диаграммах левую и правую части тождеств и сравнить их. Такой способ доказательства принято называть геометрическим.
Замечание. Практически все основные тождества (законы) множеств представлены парами, которые характеризуются своей симметричностью в отно-шении операций объединения и пересечения. Подобное свойство законов называется дуальностью (двойственностью).

Пример 5. Проверим первый дистрибутивный закон: А∪(В∩С)=(А∪В)∩(А∪С) (рис.9).
Диаграммы левой
и правой частей тождества
совпадают,
значит оно
справедливо.
Этот способ является наглядным, но не обладает достаточной строгостью.

Доказательство справедливости проверяемых тождеств можно проводить одним из двух методов:
- методом взаимного включения;
- алгебраическим методом.
Пример 6. Докажем первый дистрибутивный закон: А∪(В∩С)=(А∪В)∩(А∪С).
Обозначим левую часть тождества А∪(В∩С) через Dl, а правую – (А∪В)∩(А∪С) через Dr .
Метод взаимного включения базируется на определении равенства двух множеств, между которыми существует отношение взаимного включения: А=В ⇔А⊆В и В⊆А.

В соответствии с принятым методом доказательство разделяется на две части:
1. Пусть элемент х∈ Dl, т.е. х∈ А∪(В∩С), тогда по определению операции объединения, (х∈А) или (х∈В∩С).
1. берется произвольный элемент множества Dl (х∈Dl) и доказывается, что он принадлежит также и множеству Dr, откуда следует: Dl⊆Dr;
2. берется произвольный элемент множества Dr и доказывается, что он принадлежит также и множеству Dl, откуда следует: Dr⊆ Dl.

б) Если элемент х∈В∩С, то, по определению операции пересечения множеств, (х∈В) и (х∈С), отсюда, по определению операции объединения, (х∈А∪В) и (х∈А∪С), следовательно х∈(А∪В)∩(А∪С), т.е. х∈Dr.
Так как для любого х∈Dl следует, что х∈Dr, то, по определению отношения включения, Dl⊆Dr.
а) Если элемент х∈А, то, по определению операции объединения множеств,
(х∈А∪В) и (х∈А∪С), следовательно
х ∈ (А∪В)∩(А∪С), т.е. х∈Dr;

2. Пусть элемент х∈Dr, т.е. (х∈А∪В) и (х∈А∪С), откуда по определению операции объединения, (х∈А или х∈В) и (х∈А или х∈С), следовательно, х∈А или (х∈В и х∈С), откуда, х∈А или (х∈B∩С), т.е. х∈ А∪(В∩С) или х∈Dl, откуда Dr⊆Dl.
обозначим
Таким образом, между множествами Dl и Dr существуют отношение взаимного включения, значит Dl=Dr, что и требовалось доказать.
Пример 7.
Докажем первый закон двойственности:

1. Пусть элемент x∈Dl , т.е. x∈ . Тогда x∈U и (x∉А∪В), значит x ∉ А и х ∉ В (тонкий момент в доказательстве: х не принадлежит ни А, ни В), следовательно
Значит Dl ⊆ Dr .
2. Пусть теперь элемент х∈Dr , т.е Тогда
значит x∈U и x одновременно не принадлежит ни А, ни В, т.е. х∉(А или В), следовательно х∉А∪В, т.е. Из этого следует, что Dr ⊆ Dl.
Таким образом, между множествами Dl и Dr существуют отношение взаимного включения, значит Dl = Dr, что и требовалось доказать.

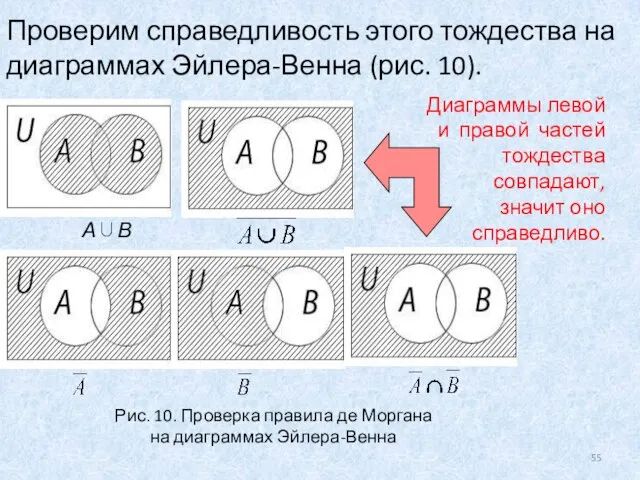
Проверим справедливость этого тождества на диаграммах Эйлера-Венна (рис. 10).
Диаграммы левой
и правой частей тождества
совпадают,
значит оно
справедливо.

А∩(А∪В)
=
⇑
свойство пустого
множества
(А∪∅)∩(А∪В)
=
⇑
по дистрибутивному
закону
(А∪(∅∩B))
=
⇑
свойство пустого
множества
А∪∅
=
⇑
А
Пример 8. Докажем второй закон поглощения: А∩(А∪В) = А путем преобразования левой части тождества к правой с использованием других тождеств:
Упорядоченные множества. Понятие вектора
Под вектором понимается упорядоченный набор элементов. Определение является не строгим (интуитивным), так же как и определение множества.

Элементы, образующие вектор, называются координатами или компонентами вектора. Число координат вектора называется его длиной или размерностью. Синонимом понятия «вектор» является «кортеж».
Для обозначения вектора обычно используются скобки, например (1, 2, 1, 3). Иногда скобки и даже запятые в обозначении вектора опускаются.
Примером векторов могут служить целые числа, при этом отдельные цифры числа являются координатами этого вектора.
Замечание. В отличие от элементов множеств, некоторые координаты вектора могут совпадать.

Векторы длины два называются упорядоченными парами (или просто парами), длины три – тройками, …, длины n – n-ками и т.д.
Два вектора равны, если они имеют одинаковую длину и соответствующие их координаты равны, т.е. (а1, а2, …, аm) = (b1, b2,…,bn), если m = n и
a1 = b1, a2 = b2, …, am = bm.
Векторы (кортежи) образуют особый класс множеств, называемых упорядоченными. В отличии от множеств, элементы которых могут быть перечислены в произвольном порядке, для элементов (координат) вектора существенным является их положение внутри вектора.

В связи с этим множества, содержащие одинако-вые элементы, но в различном порядке, равны
{a, b} = {b, a}, а вектора – нет (a, b) ≠ (b, a).
Прямое (декартово) произведение множеств
Прямым (декартовым) произведением множеств А и В называется множество всех пар (а, b), таких, что а∈А и b∈В.
Прямое произведение множеств А и В обозначает-ся в виде А×В: А×В = {(a, b)⏐a∈A и b∈B}.
Пример 9. А = {a, b, c}; B ={b, c}.
A×B = {(a, b), (a, c), (b, b), (b, c), (c, b), (c, c)};
B×A = {(b, a}, (b, b), (b, c), (c, a), (c, b), (c, c)}.

Замечание. Из рассмотренного примера видно, что А×В ≠ В×А, т.е. коммутативный закон для прямого произведения множеств не действует.
Пример 10. Х – множество точек отрезка [0;1];
Y – множество точек отрезка [1;2].
Тогда Х×Y – множество точек квадрата с вершинами в точках (0,1), (0,2), (1,1), (1,2).
Декартова степень множества
Прямое (декартово) произведение одинаковых множеств называется декартовой степенью множества: если В = А, то А×В = А×А = А2.

Точка на плоскости может быть задана упорядо-ченной парой координат, т.е. двумя точками на координатных осях. Так как координаты представ-ляются множеством действительных чисел R, то прямое произведение R×R = R2 представляет собой множество координат точек плоскости.
Прямым (декартовым) произведением множеств А1, А2, …, Аn называется совокупность всех упорядоченных n-ок (векторов длиной n) (a1, a2, …, an) таких, что ai∈Ai (i=1,2,…,n). В случае, если А1=А2=…=Аn=А, то А1×А2×…×Аn = Аn - n-ая декартова степень множества А.

Пример 11.
Х – множество точек отрезка [0;1];
Y – множество точек отрезка [1;2];
Z – множество точек отрезка [0;0,5].
X×Y×Z – множество точек пространства, ограниченного параллелепипедом.
Замечание. Декартово произведение R×R×R= R3 представляет собой множество координат точек пространства.

Тогда мощность их прямого произведения равна произведению мощностей множеств – сомножителей, т.е. ⏐А1×А2×…×Аn⏐=m1⋅m2 ⋅ … ⋅ mn.
Мощность прямого произведения множеств
Теорема. Пусть А1, А2, …, Аn – конечные множества мощностью m1, m2, …, mn. соответственно, т.е. ⏐А1⏐= m1,⏐A2⏐= m2, …,⏐An⏐= mn.
Основные тождества для операции
прямого произведения множеств
(А∩В) × (C∩D) = (А×C) ∩ (B×D);
(А∪В) × C = (А×C) ∪(B×C);
(А\В) × C = (А×C) \(B×C);
А×(В\C) = (А×B) \(A×C).