Содержание
- 2. Определение. Уравнения вида f(x) = а, где а – данное число, а f(x) – одна из
- 3. Решение простейших тригонометрических уравнений.
- 4. 14.12.2020 2) уметь определять значения синуса, косинуса, тангенса и котангенса для точек числовой окружности; 4) знать
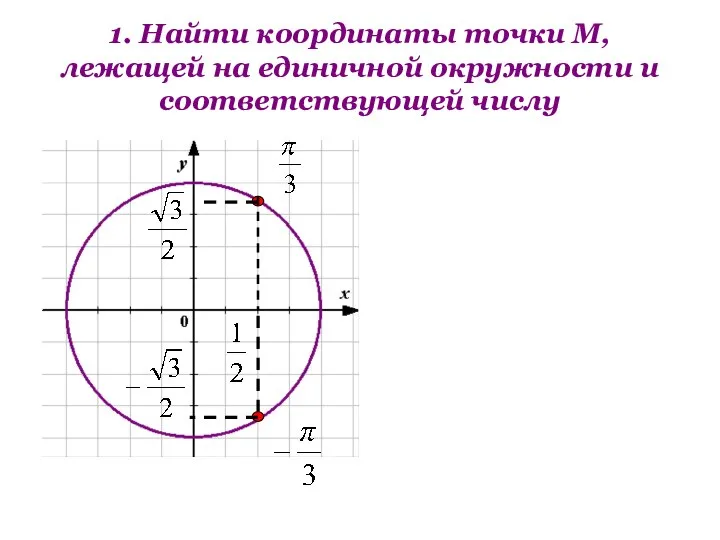
- 5. 1. Найти координаты точки М, лежащей на единичной окружности и соответствующей числу
- 6. 2. Дана точка М с абсциссой ½. Найдите ординату этой точки; укажите три угла поворота, в
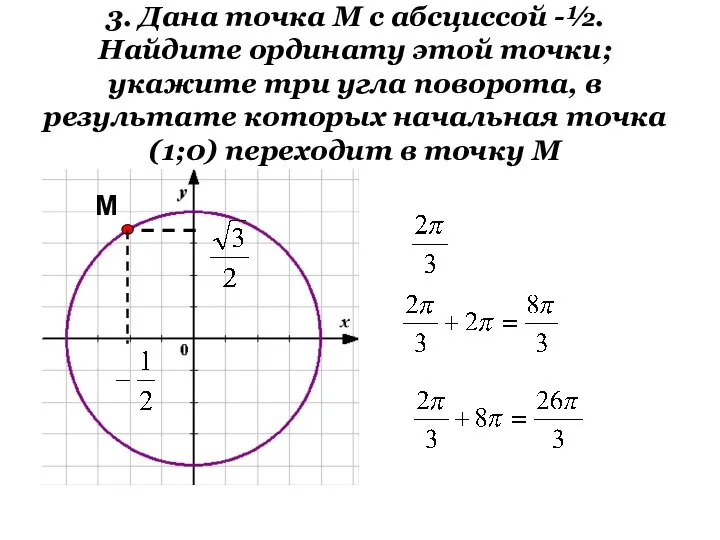
- 7. 3. Дана точка М с абсциссой -½. Найдите ординату этой точки; укажите три угла поворота, в
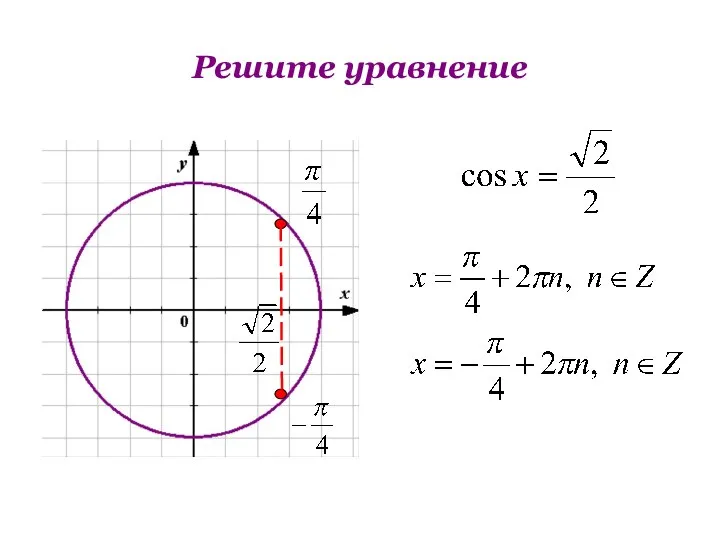
- 8. Решите уравнение
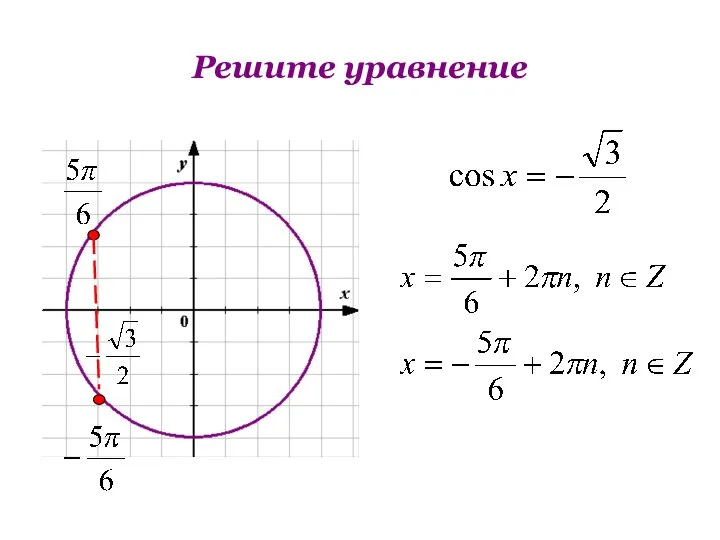
- 9. Решите уравнение
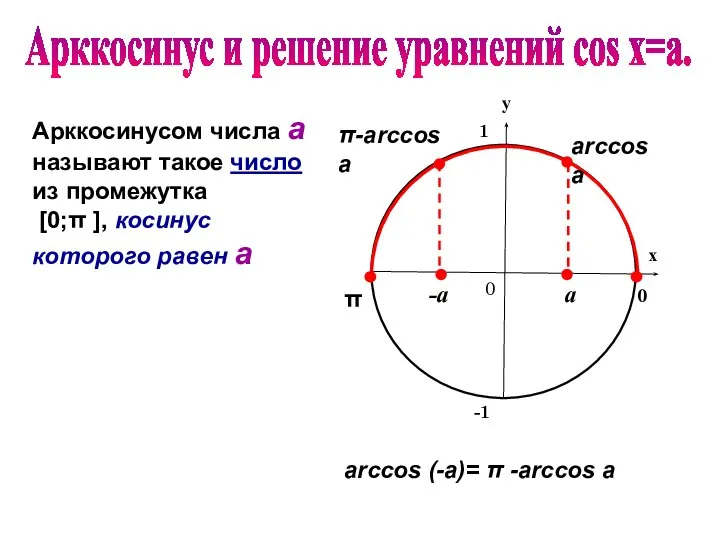
- 10. π 0 arccos а Арккосинусом числа а называют такое число из промежутка [0;π ], косинус которого
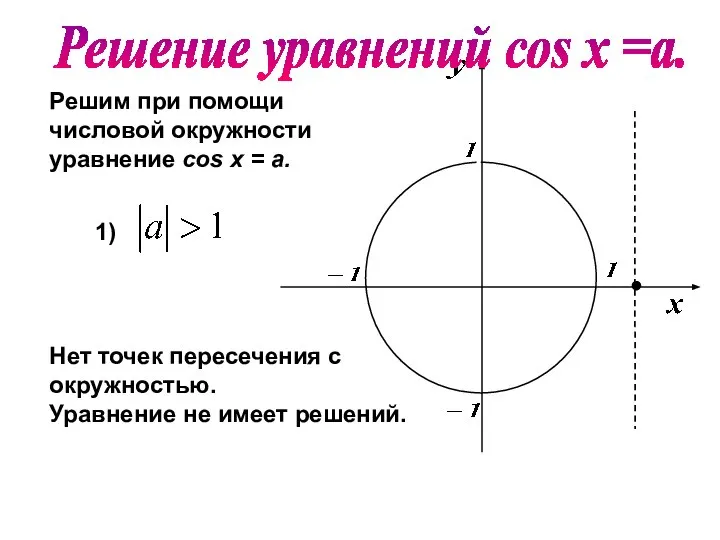
- 11. Решим при помощи числовой окружности уравнение cos х = a. 1) Нет точек пересечения с окружностью.
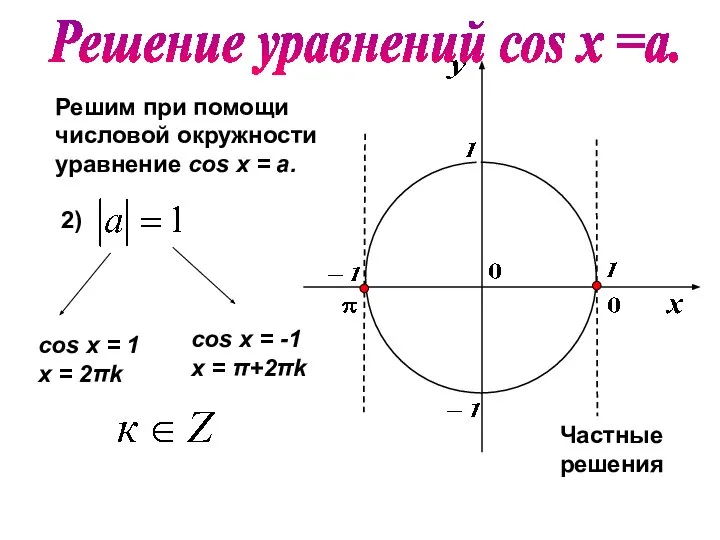
- 12. Решим при помощи числовой окружности уравнение cos х = a. 2) cos х = 1 х
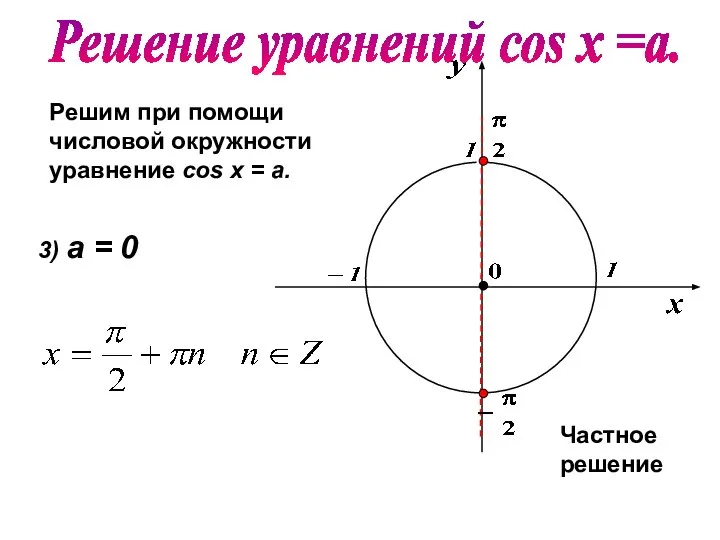
- 13. Решим при помощи числовой окружности уравнение cos х = a. 3) а = 0 Частное решение
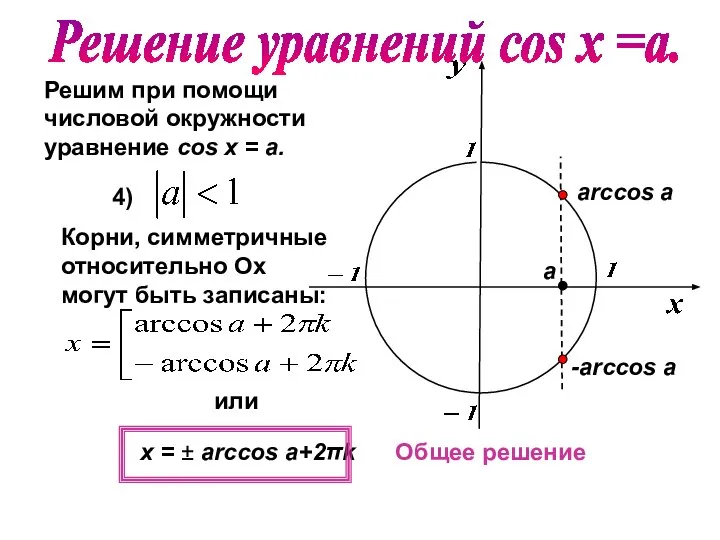
- 14. Решим при помощи числовой окружности уравнение cos х = a. 4) Общее решение arccos а -arccos
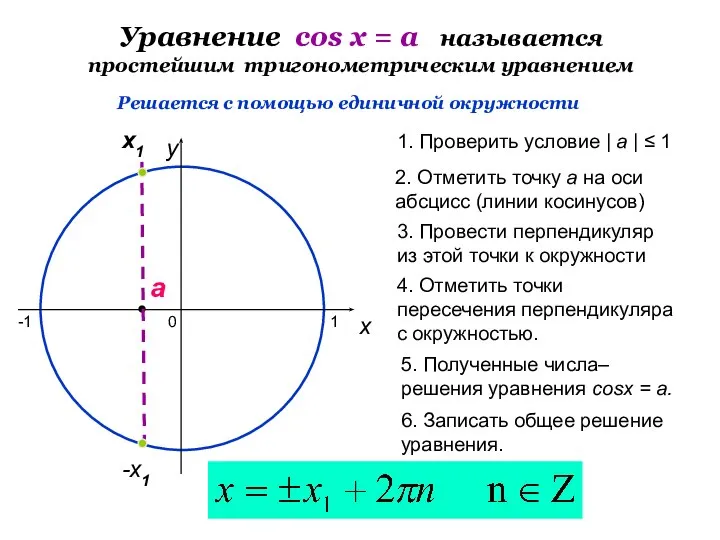
- 15. Уравнение cos х = a называется простейшим тригонометрическим уравнением 0 x y 2. Отметить точку а
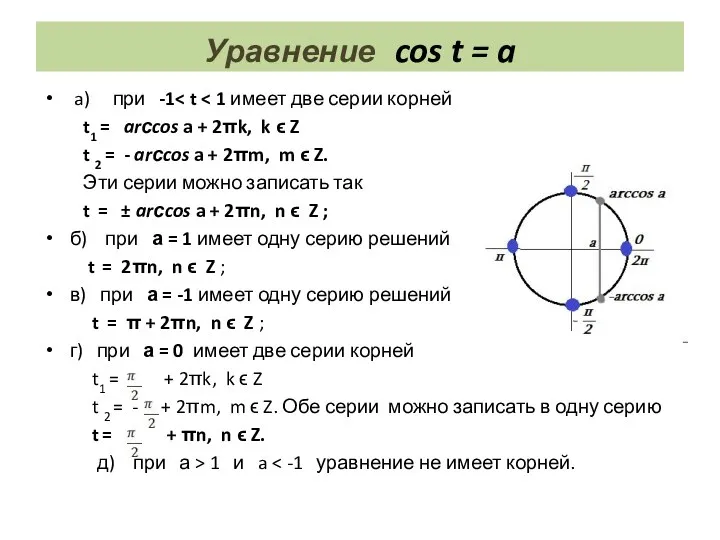
- 16. Уравнение cos t = a a) при -1 t1 = arсcos a + 2πk, k ϵ
- 17. Решите уравнение 1) cos х = 2) cos х = -
- 18. Решите уравнение 3) cos 4x = 1 4x = 2πn, n ϵ Z 4)
- 19. Решите уравнение 5) .
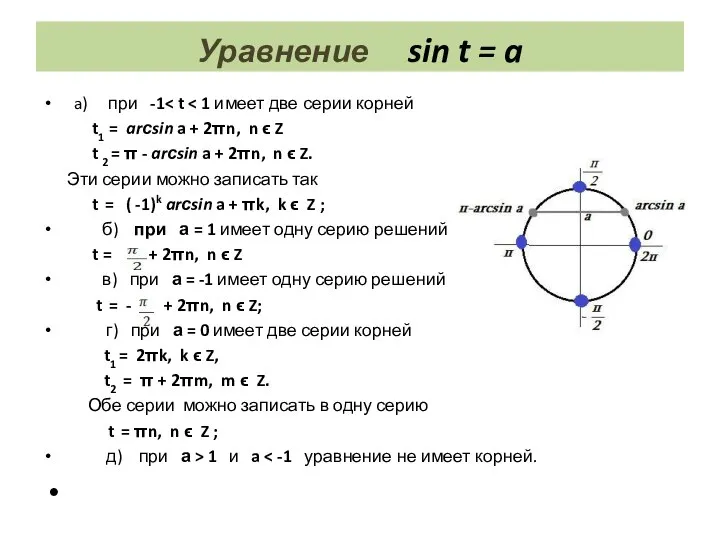
- 20. Уравнение sin t = a a) при -1 t1 = arсsin a + 2πn, n ϵ
- 21. Решите уравнение sin х = , , x = ( -1)k + πk, k ϵ Z
- 22. Решите уравнение 2) sin х = - x = ( -1)k+1 ; , , ; x
- 23. Задание 2. Найти корни уравнения: 1) a) sin x =1 б) sin x = - 1
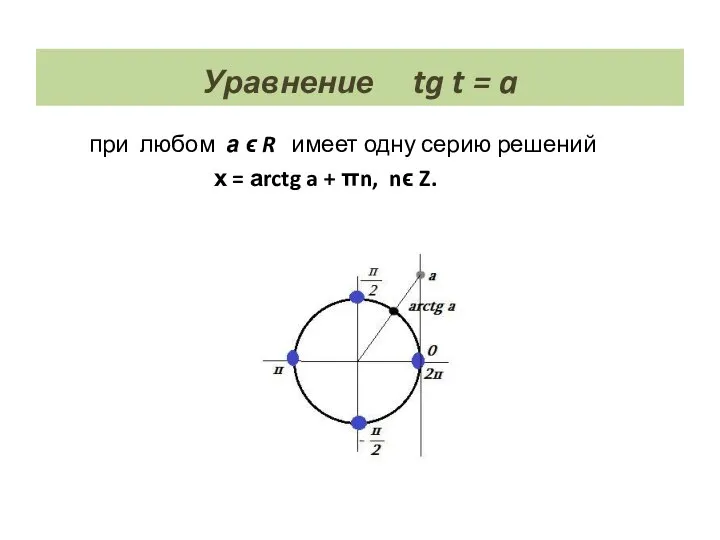
- 24. Уравнение tg t = a при любом а ϵ R имеет одну серию решений х =
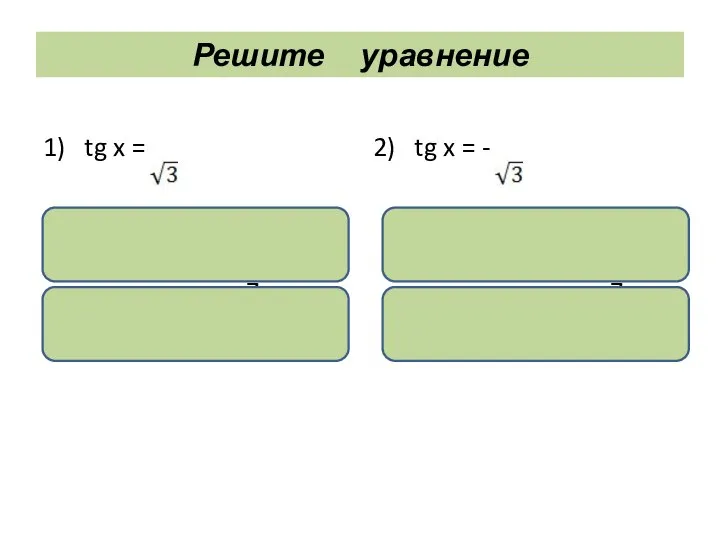
- 25. Решите уравнение 1) tg x = х = аrctg + πn, nϵ Z. x = +
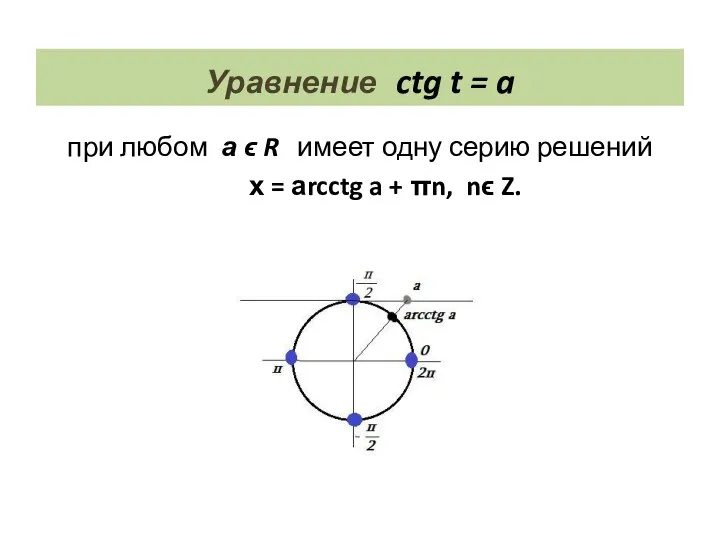
- 26. Уравнение ctg t = a при любом а ϵ R имеет одну серию решений х =
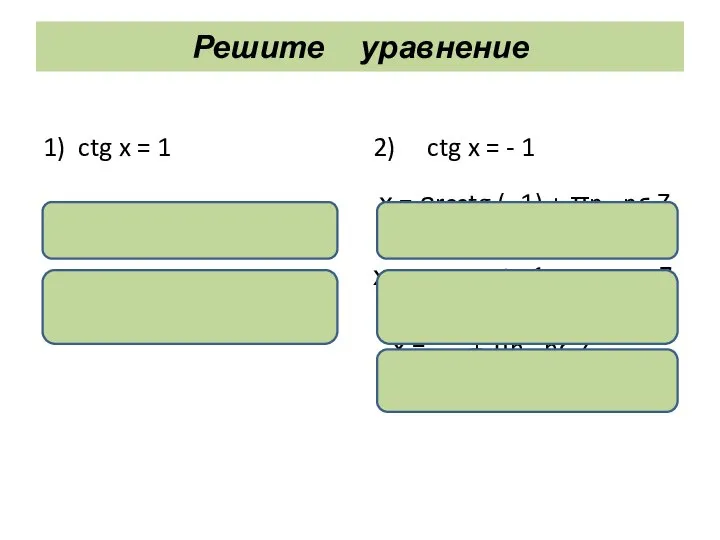
- 27. Решите уравнение 1) ctg x = 1 х = аrcctg 1 + πn, nϵ Z, х
- 29. Скачать презентацию










 Словесный способ задания последовательности. Аналитический способ задания последовательности
Словесный способ задания последовательности. Аналитический способ задания последовательности Стереометрия. Практическая работа
Стереометрия. Практическая работа Презентация на тему Степени
Презентация на тему Степени  Равнобедренный треугольник и его свойства, 7 класс
Равнобедренный треугольник и его свойства, 7 класс Сокращение дробей. Самоанализ
Сокращение дробей. Самоанализ Задачи на готовых чертежах (геометрия, 7 класс)
Задачи на готовых чертежах (геометрия, 7 класс) Математические головоломки. Математика вокруг нас
Математические головоломки. Математика вокруг нас Образование дробей. 5 класс
Образование дробей. 5 класс Векторы. Обобщающий урок
Векторы. Обобщающий урок Тела вращения. Цилиндр. Площадь поверхности цилиндра
Тела вращения. Цилиндр. Площадь поверхности цилиндра Урок - путешествие В поиске клада
Урок - путешествие В поиске клада Логарифм числа и его свойства
Логарифм числа и его свойства Решение задач ЕГЭ по тригонометрии
Решение задач ЕГЭ по тригонометрии Умножение на 2 и 3. Закрепление
Умножение на 2 и 3. Закрепление Урок математики
Урок математики Вычитание числа 2 (1 класс)
Вычитание числа 2 (1 класс) Обыкновенная дробь
Обыкновенная дробь SLUChAJNYE_VELIChINY
SLUChAJNYE_VELIChINY Теория вероятностей
Теория вероятностей Решение задач по теме Длина окружности, длина дуги окружности
Решение задач по теме Длина окружности, длина дуги окружности Квадартные уравнения. Основные понятия
Квадартные уравнения. Основные понятия Презентация на тему Деление многозначного числа на однозначное
Презентация на тему Деление многозначного числа на однозначное  Решение неравенств с модулем
Решение неравенств с модулем Многоугольники. Виды многоугольников
Многоугольники. Виды многоугольников Производная функции
Производная функции Решение логарифмических уравнений
Решение логарифмических уравнений Квадратные уравнения
Квадратные уравнения Презентация на тему Свойства прямоугольного параллелепипеда
Презентация на тему Свойства прямоугольного параллелепипеда