Дискретные случайные величины

Цель занятия:
Познакомиться с понятием дискретной случайной величины, научиться составлять её закон распределения, вычислять числовые характеристики дискретной случайной величины.

Случайное событие, связанное с некоторым опытом, является качественной характеристикой опыта.
Количественной же характеристикой результата проведенного опыта является случайная величина, к рассмотрению которой мы приступаем.

Определение 1. Случайной называется величина, которая в результате опыта принимает с определенной вероятностью то или иное значение , зависящее от исхода опыта.
Обозначения случайных величин:
X, Y, Z,.., а их значений соответственно: x, y, z, …

Пример 1. Игрок бросает монету – при выпадении герба он выигрывает 1 рубль, решки – проигрывает 1 рубль. Случайная величина Х – выигрыш игрока будет принимать значения +1 или -1 в зависимости от того, чем закончится эксперимент – гербом или решкой.
Пример 2. Эксперимент – одновременное бросание двух игральных кубиков, случайная величина – сумма выпавших очков, может принимать все целые значения от 2 до 12 в зависимости от выпавшей комбинации.

Пример 3. Эксперимент – n-кратное повторение опыта с бросанием монеты, случайная величина – количество выпавших гербов – может принимать все целые значения от 0 до n.
Пример 4. Эксперимент – извлечение шара из урны, содержащей равное количество белых и черных шаров, с возвращением шара в урну после каждого извлечения. Случайная величина – количество извлечений до первого появления белого шара.
Эта случайная величина может принимать …
все целые положительные значения: 1, 2, 3, …, n, …

Пример 5. Эксперимент – случайный выбор точки из отрезка [0; 1]. Случайная величина – координата точки. Эта случайная величина может принимать …
любые значения от 0 до 1.
Пример 6. Эксперимент – наблюдение за временем безотказной работы некоторого устройства: от момента включения до первого выхода из строя. Случайная величина – время безотказной работы – может принимать …
все действительные числа от 0 до +∞.

Определение 2. Случайная величина называется дискретной, если множество ее значений конечно или счетно, т.е. множество ее значений представляет собой конечную последовательность
х1, х2, …, хn или бесконечную последовательность х1, х2, …, хn, …
Вероятность того, что случайная величина Х примет значение х, обозначают
Р(х) = Р(Х = х).

Определение 3. Соответствие между возможными значениями х1, х2, …, хn случайной величины Х и их вероятностями р1, р2, …, рn называется законом распределения случайной величины Х.
Закон распределения случайной величины может быть представлен в виде таблицы

События Х = х1, Х = х2, …, Х = хn образуют полную систему попарно несовместных событий, поэтому сумма их вероятностей равна единице, т.е.
р1 + р2 + … + рn = 1.
х1
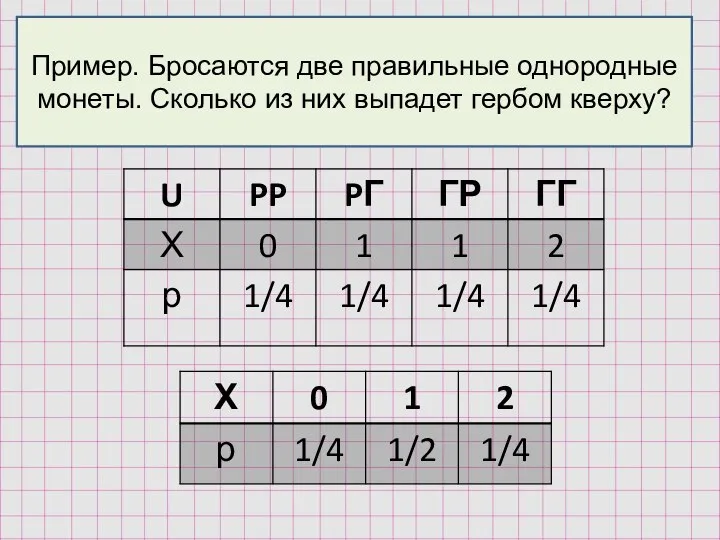
х1

Пример. Бросаются две правильные однородные монеты. Сколько из них выпадет гербом кверху?

Над случайными величинами устанавливаются операции сложения и умножения
1. Суммой двух случайных величин X и Y называется случайная величина, которая получается в результате сложения всех значений случайной величины Х и всех значений случайной величины Y, соответствующие вероятности перемножаются.
2. Произведением двух случайных величин X и Y называется случайная величина, которая получается в результате перемножения всех значений случайной величины Х и всех значений случайной величины Y, соответствующие вероятности перемножаются.

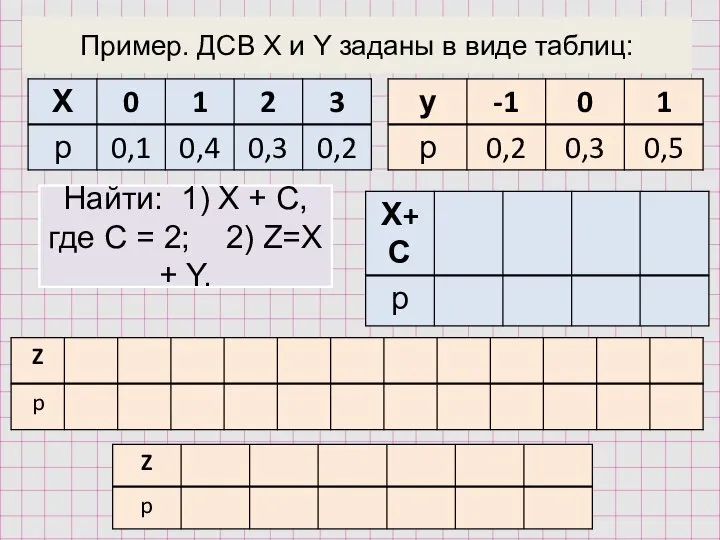
Пример. ДСВ X и Y заданы в виде таблиц:
Найти: 1) Х + С, где С = 2; 2) Z=X + Y.

Биномиальное распределение
Пусть случайная величина Х – число появлений события А в n независимых испытаниях, в каждом из которых вероятность появления события А равна р, а непоявления равна q = 1 – p. Очевидно, что Х может принимать значения 0, 1, 2, …, n, вероятности которых определяются по формуле Бернулли:

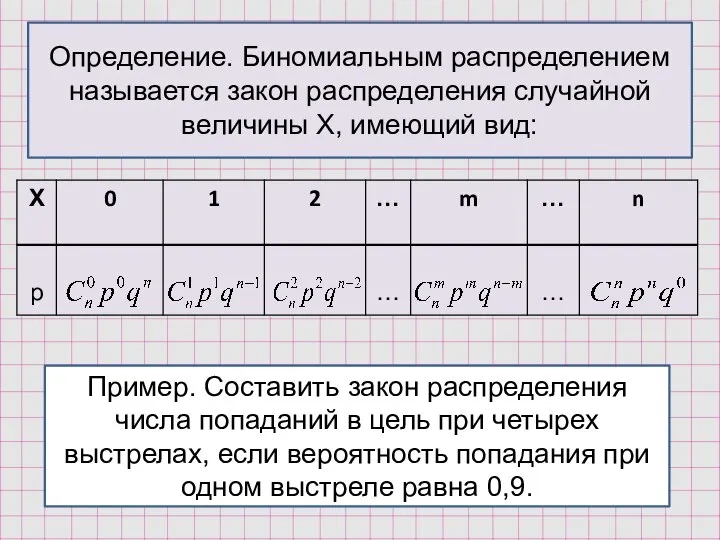
Определение. Биномиальным распределением называется закон распределения случайной величины Х, имеющий вид:
Пример. Составить закон распределения числа попаданий в цель при четырех выстрелах, если вероятность попадания при одном выстреле равна 0,9.

Пример. Монета бросается 5 раз, представим закон распределения ДСВ Х – числа появления герба, в виде таблицы.

Пример. Составить закон распределения числа попаданий в цель при четырех выстрелах, если вероятность попадания при одном выстреле равна 0,9.

Упражнения.
1. Составить закон распределения числа попаданий в цель при шести выстрелах, если вероятность попадания при одном выстреле равна 0,8.
2. Вероятность того, что студент найдет в библиотеке нужную ему книгу, равна 0,3. Составить закон распределения числа библиотек, которые он посетит, если в городе четыре библиотеки.

Числовые характеристики
распределения дискретных случайных величин

На практике нет необходимости характеризовать случайную величину полностью. Обычно достаточно указать только отдельные числовые параметры распределения ее значений. Такие числовые параметры называются числовыми характеристиками распределения. Прежде всего, это характеристики положения: математическое ожидание, медиана, мода; характеристики рассеяния: дисперсия, среднее квадратическое отклонение.

Определение. Математическим ожиданием М(Х) дискретной случайной величины Х называется сумма произведений всех ее возможных значений хi на их вероятности pi:
М(Х) = х1р1 + х2р2 + … + хnрn=∑ хiрi
Пример. Найти математическое ожидание случайной величины Х, зная ее закон распределения:

Свойства математического ожидания
1. Постоянный множитель можно выносить за знак математического ожидания: М(СХ) = С М(Х).
2. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий:
М(X + Y) = M (X) + M (Y).
3. Математическое ожидание постоянной величины С равно самой этой величине: М (С) = С.

4. Математическое ожидание любой линейной комбинации случайных величин равно линейной комбинации их математических ожиданий:
М (∑ Сk Хk) = ∑ (Сk M (Хk)).
5. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий:
M (XY) = M (X) M(Y).

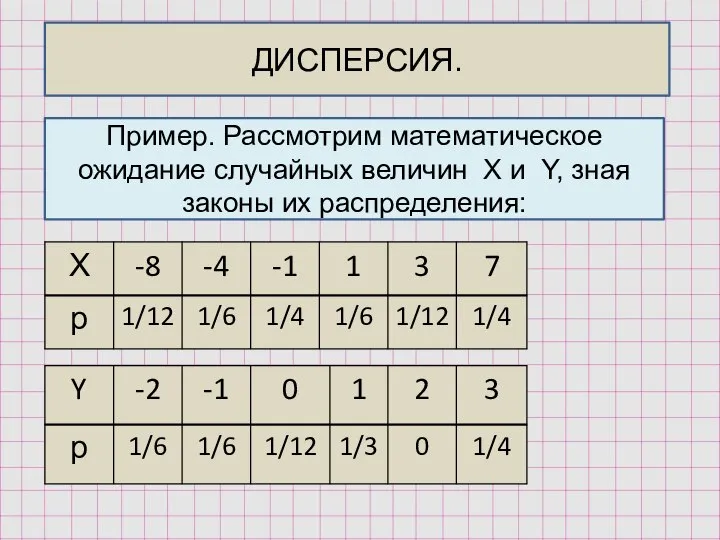
ДИСПЕРСИЯ.
Пример. Рассмотрим математическое ожидание случайных величин X и Y, зная законы их распределения:

Основной числовой характеристикой степени рассеяния значений случайной величины Х относительно ее математического ожидания М(Х) является дисперсия, которая обозначается D (X).
Определение. Отклонением называется разность между случайной величиной Х и ее математическим ожиданием М (Х), т.е. Х – М (Х).
Определение. Дисперсией дискретной случайной величины Х называется математическое ожидание квадрата ее отклонения: D (X) = М (Х – М (Х))2.