Уравнение tg x = a

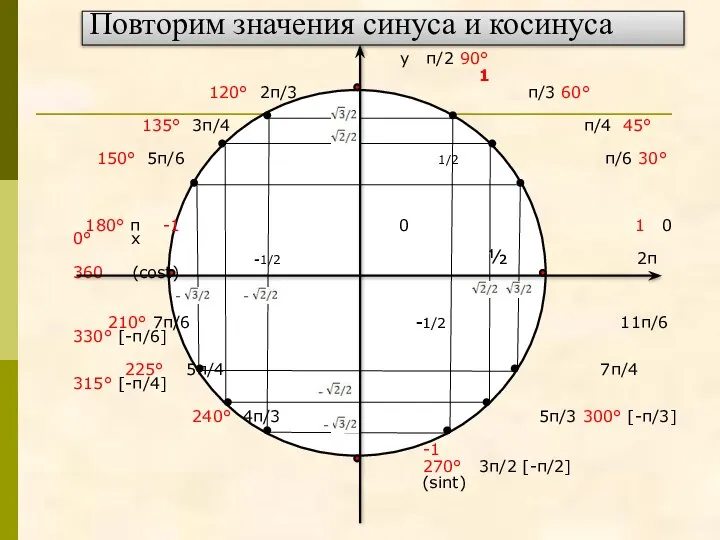
Повторим значения синуса и косинуса
у π/2 90°
1
120° 2π/3 π/3 60°
135° 3π/4 π/4 45°
150° 5π/6 1/2 π/6 30°
180° π -1 0 1 0 0° x
-1/2 ½ 2π 360 (cost)
210° 7π/6 -1/2 11π/6 330° [-π/6]
225° 5π/4 7π/4 315° [-π/4]
240° 4π/3 5π/3 300° [-π/3]
-1
270° 3π/2 [-π/2]
(sint)

Определение арктангенса
tg(arctg a) = a
arctg (−a) = − arctg a

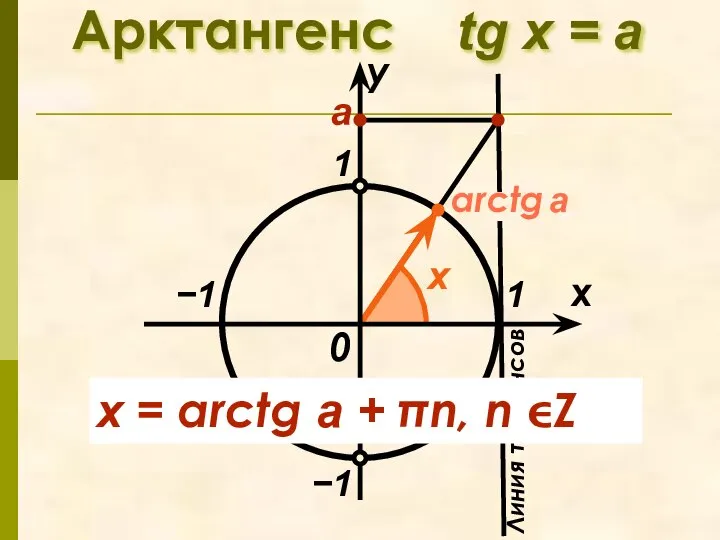
arctg a
Арктангенс tg x = а
1
x
у
0
x
Линия тангенсов
а
−1
−1
1
x = arctg a + πn, n Z

Частные случаи
tg x=0
x=πn, n Z
tg x=-1
x=-π\4+ πn, n Z
tg x=1
x=π\4+ πn, n Z

Определение арккотангенса
Арккотангенсом числа а называется
такой угол из промежутка (0; π),
котангенс которого равен а.
arcсtg a = x, сtg x = a
где x∈ (0; π)
сtg(arсctg a) = a
arcсtg(сtg x) = x, x ∈ (0; π)
arсctg (−a) = π − arcсtg a

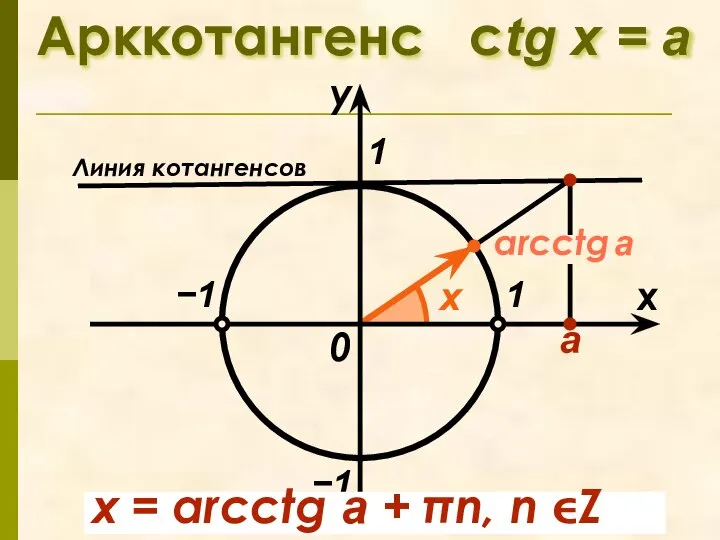
arcctg a
Арккотангенс сtg x = а
1
x
у
0
x
Линия котангенсов
а
−1
−1
1
x = arcсtg a + πn, n Z

Частные случаи
ctg x=0
x= π\2+ πn, n Z
ctg x=-1
x=-π\4+ πn, n Z
ctg x=1
x=π\4+ πn, n Z

Решим уравнение
tg x=√3
x = arctg a + πn, n Z
x = arctg√3+ πn, n Z
x = π\3+ πn, n Z
Ответ: π\3+ πn, n Z.

Решим уравнение
(tg x-1)(tg x+√3)=0
tg x-1=0 или tg x+√3=0
tg x=1 или tg x=-√3
х=π\4+ πn, n Z или x = -π\3+ πк, к Z
Ответ: -π\3+ πк, π\4+ πn, n ,к Z