Движение в пространстве

Теория

Основные теоремы о задании движений пространства:
Теорема 1. Пусть в пространстве даны два равных треугольника ABC и A'B'C'. Тогда существуют два и только два таких движения пространства, которые переводят A в A', B в B', C в C'. Каждое из этих движений получается из другого с помощью композиции его с отражением в плоскости A'B'C'
Теорема 2. Пусть в пространстве заданы два равных тетраэдра ABCD и A'B'C'D'. Тогда существует единственное движение пространства (такое, что ((A) = A', ((B) = B', ((C) = C', ((D) = D'

Неподвижные точки движений пространства.
Важной характеристикой движения пространства является множество его неподвижных точек. Здесь могут представиться лишь следующие пять случаев:
1.У движения неподвижных точек нет (нетождественный параллельный перенос)
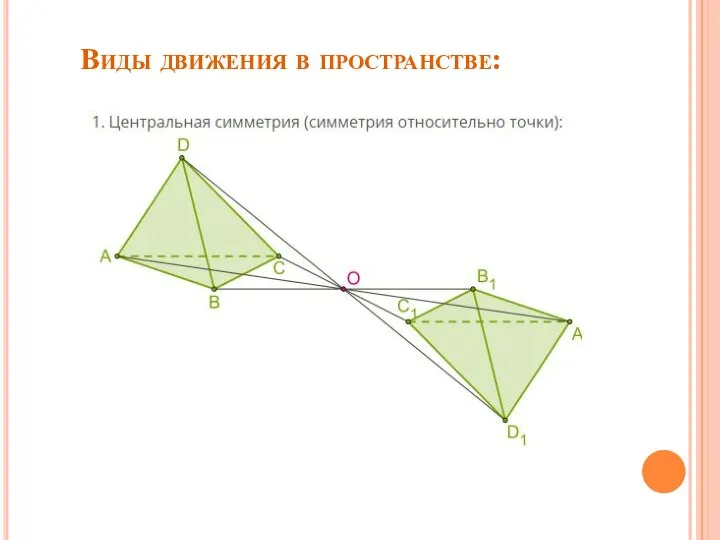
2.Движение имеет лишь одну неподвижную точку (центральная симметрия)
3.Множество неподвижных точек движения пространства является прямой (поворот вокруг прямой)
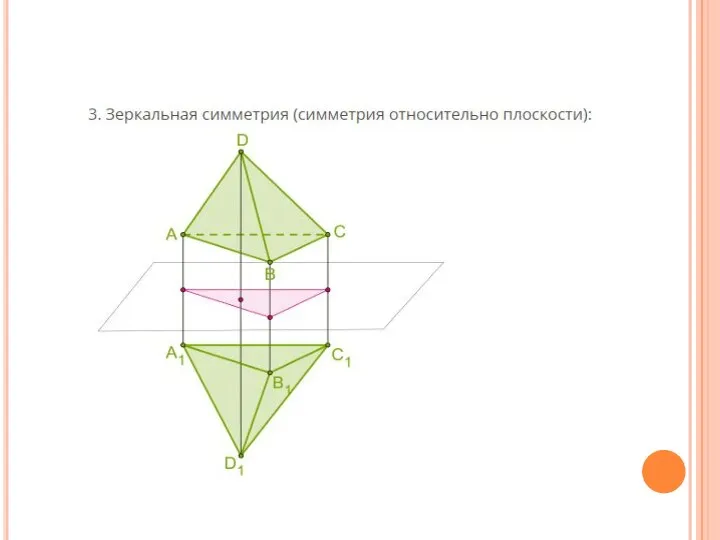
4.Множество неподвижных точек движения пространства является плоскостью (зеркальная симметрия)
5.Множество неподвижных точек движения пространства является всем пространством (тождественное движение)

Виды движения в пространстве: