Содержание
- 2. Теорема Пуассона Биномиальная случайная величина с параметрами N и p. Пусть число N неограниченно возрастает, при
- 3. Предельный переход при N → ∞ Вынесем общий множитель, не содержащий N
- 4. a = N p Параметр распределения Пуассона равен произведению параметров распределения Бернулли: Вывод: при большом значении
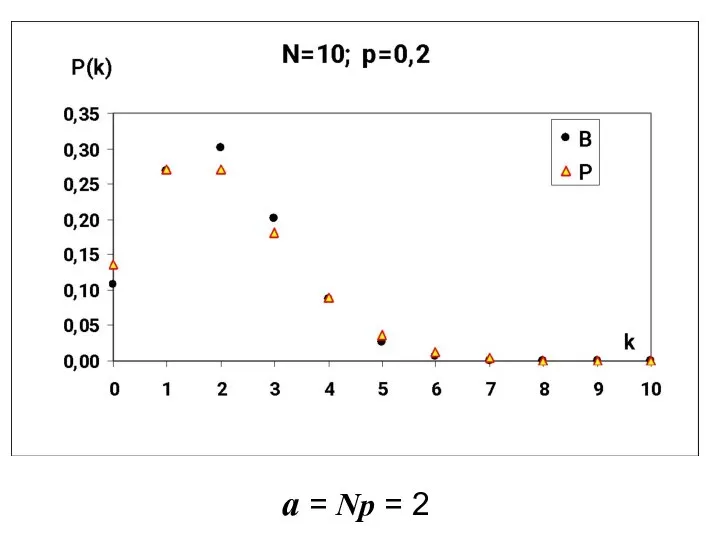
- 5. a = Np = 2
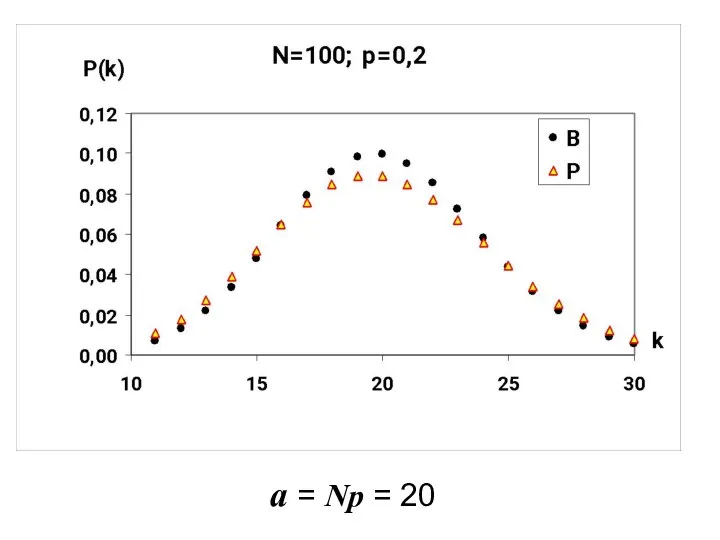
- 6. a = Np = 20
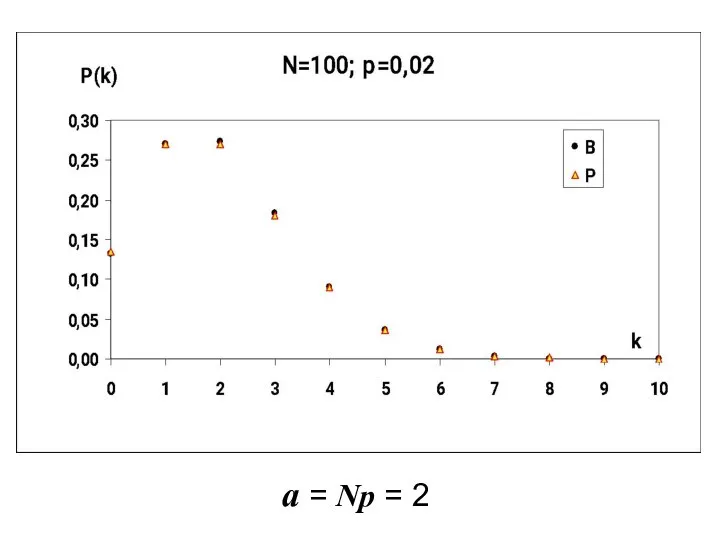
- 7. a = Np = 2
- 8. Хорошее совпадение распределения Бернулли с распределением Пуассона наблюдается при значении параметра N > 100 , и
- 9. Теорема Муавра – Лапласа Биномиальная случайная величина с параметрами N и p. Вероятность того, что значение
- 10. где: μ = Np, σ2 = Np(1– p) Согласно теореме Муавра – Лапласа, справедлив следующий предельный
- 11. Это означает, что при очень больших значениях параметра N и при большом значении произведения параметров Np
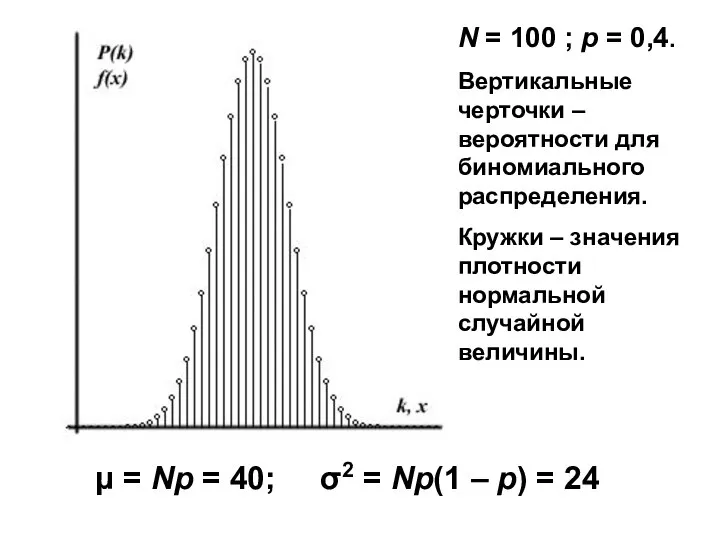
- 12. N = 100 ; p = 0,4. Вертикальные черточки – вероятности для биномиального распределения. Кружки –
- 13. Как вычислить определенный интеграл в правой части теоремы Муавра-Лапласа? Замена переменной: z = (x – μ)
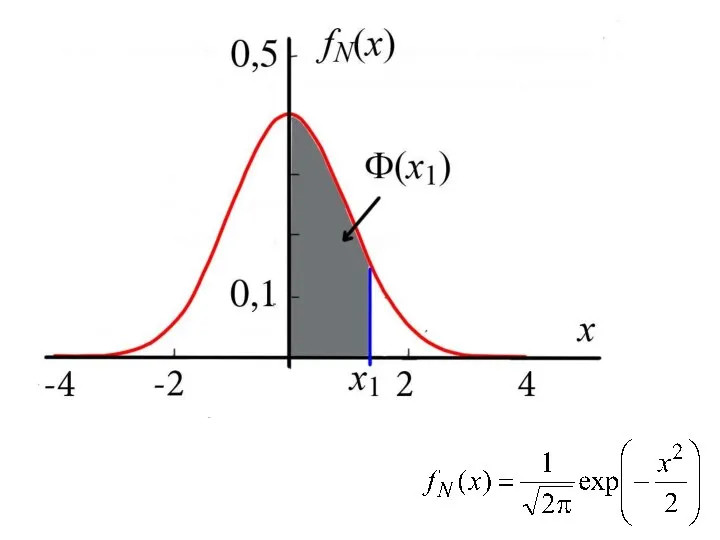
- 14. Функция Лапласа Интеграл с переменным верхним пределом от нормированной функции Гаусса Это плотность гауссовой случайной величины
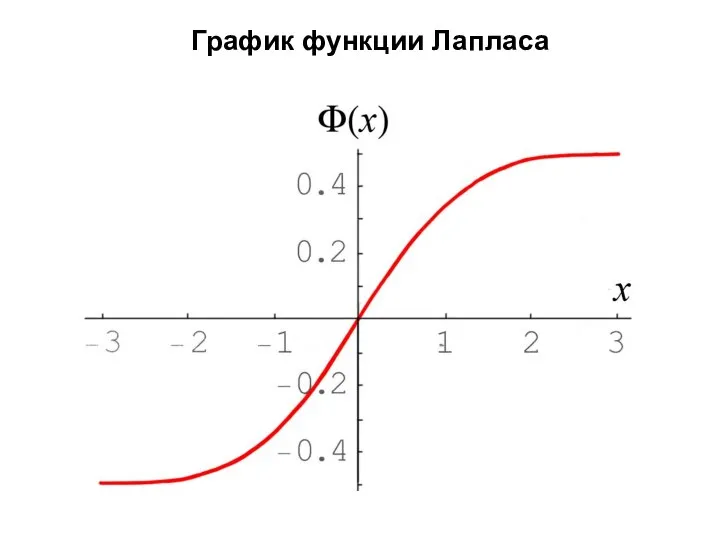
- 15. Свойства функции Лапласа Φ(x=0) = 0 2. Φ(−x) = − Φ(x). 3. Функция Лапласа быстро стремится
- 17. График функции Лапласа
- 18. k - значение биномиальной случайной величины с параметрами N и p. где Ф – функция Лапласа,
- 19. Центральная предельная теорема
- 20. i ; (i = 1, …, N ) – случайные величины Если N → ∞, то
- 21. Теорема 1 i ; (i = 1, …, N ) – попарно независимые случайные величины, имеющие
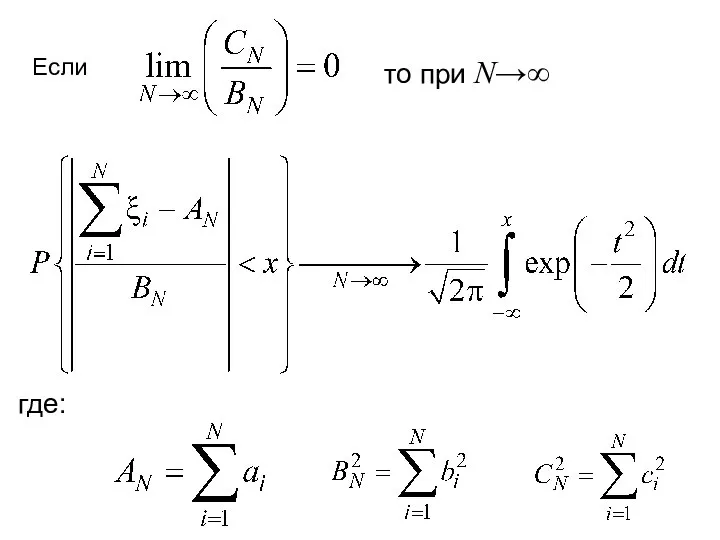
- 22. Теорема 2 (теорема Ляпунова) i ; (i = 1, …, N ) – независимые случайные величины.
- 23. Если то при N→∞ где:
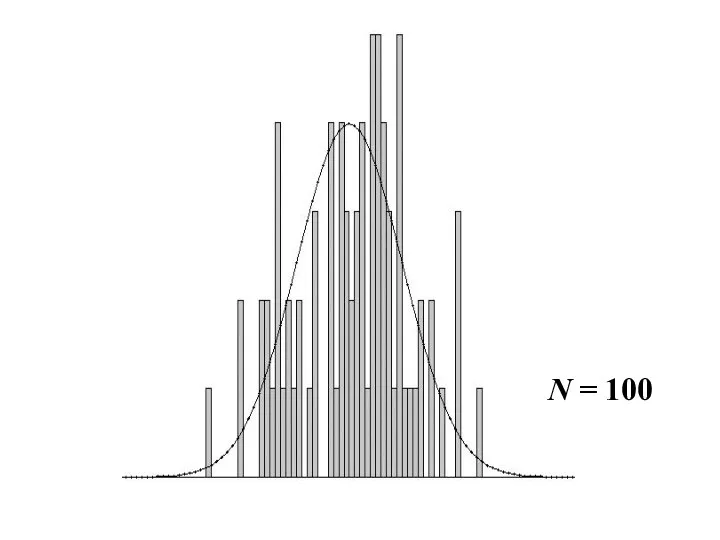
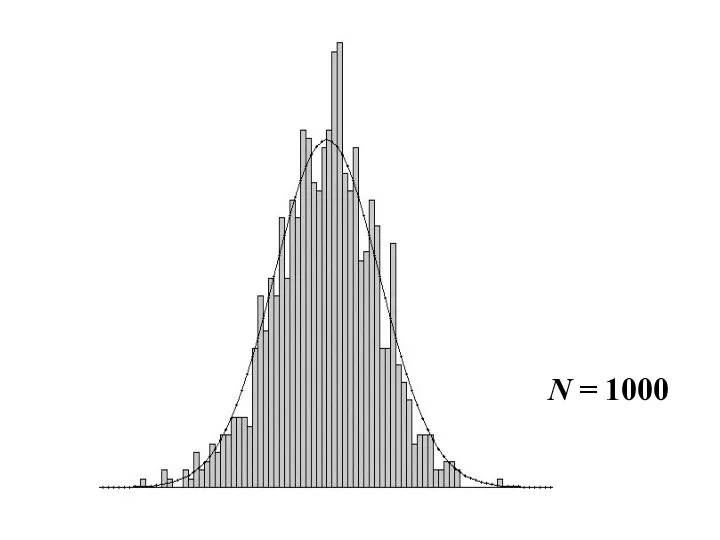
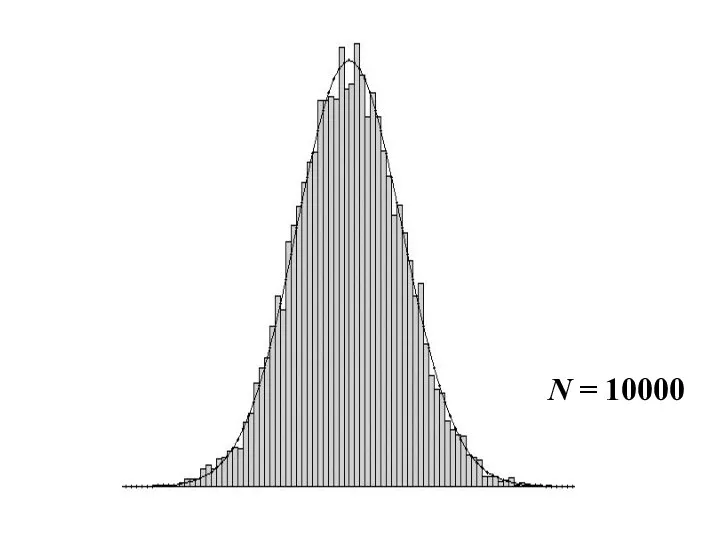
- 24. Нормированная сумма любых независимых случайных величин при N→∞ имеет нормальное распределение. На следующих слайдах показаны графики
- 25. N = 100
- 26. N = 1000
- 27. N = 10000
- 29. Скачать презентацию
















 МХСИ
МХСИ Подготовка к ПА. Математика
Подготовка к ПА. Математика Объём цилиндра. Решение задач
Объём цилиндра. Решение задач Пирамида
Пирамида Уравнения. 3 класс
Уравнения. 3 класс Построение графика функции
Построение графика функции Задачи. 1 класс
Задачи. 1 класс Презентация на тему Перпендикуляр и наклонная 10 класс
Презентация на тему Перпендикуляр и наклонная 10 класс  Сравнение десятичных дробей
Сравнение десятичных дробей Экстремум функции двух переменных. Задания
Экстремум функции двух переменных. Задания Математика в биологии
Математика в биологии Решение задач на нахождение площадей фигур
Решение задач на нахождение площадей фигур Упрощение логических выражений
Упрощение логических выражений Презентация по математике "Решение задач на разностное и кратное сравнение чисел" -
Презентация по математике "Решение задач на разностное и кратное сравнение чисел" -  Алгоритм расчета аппроксимирующей функции I-интеграла и L-интеграла
Алгоритм расчета аппроксимирующей функции I-интеграла и L-интеграла Взвешенные графы. Остовные деревья. Кратчайшие пути
Взвешенные графы. Остовные деревья. Кратчайшие пути Математическая физминутка
Математическая физминутка Сложение и вычитание. Разминка
Сложение и вычитание. Разминка Показательная функция
Показательная функция Показательная функция
Показательная функция Презентация на тему Геометрические построения в школьном курсе математики
Презентация на тему Геометрические построения в школьном курсе математики  Презентация на тему Действия с рациональными числами
Презентация на тему Действия с рациональными числами  Квадратные уравнения
Квадратные уравнения Применение производной к исследованию функции
Применение производной к исследованию функции Комбинаторика. 11 класс
Комбинаторика. 11 класс Показательная функция, её свойства и график. Логарифмическая функция, ее свойства и график
Показательная функция, её свойства и график. Логарифмическая функция, ее свойства и график Мир отрицательных чисел
Мир отрицательных чисел Площадь круга
Площадь круга