Метод деформируемого многогранника (Нелдера-Мида)

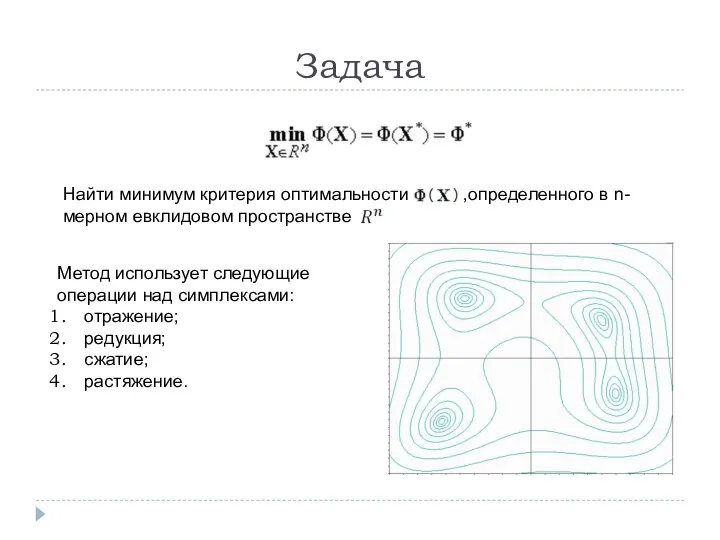
Задача
Найти минимум критерия оптимальности ,определенного в n-мерном евклидовом пространстве
Метод использует следующие операции над симплексами:
отражение;
редукция;
сжатие;
растяжение.

Отражение вершин симплекса
Производится относительно центра тяжести остальных вершин.
Отражение k-й вершины с координатами:
Вектор координат центра тяжести остальных вершин симплекса:
Новый симплекс с координатами вершин:

Редукция симплекса
Уменьшение длин всех ребер симплекса в одно и то же количество раз.
Редукция вершин симплекса к вершине
Коэффициенты редукции равны:
Новый симплекс с координатами вершин:

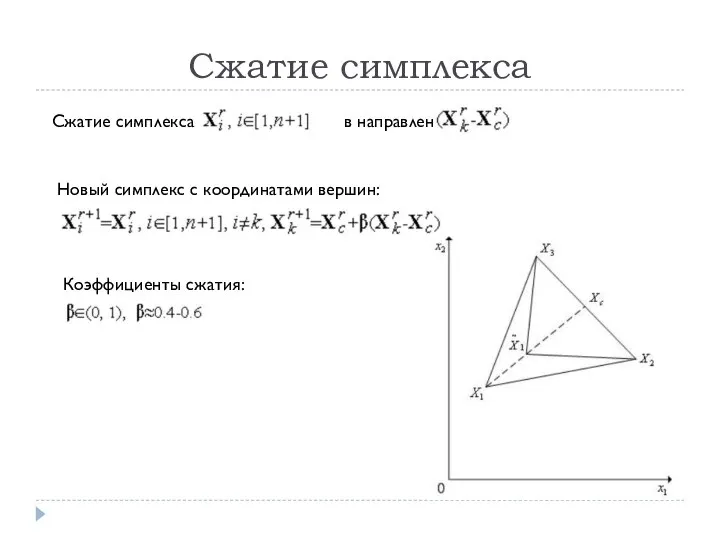
Сжатие симплекса
Сжатие симплекса в направлении
Новый симплекс с координатами вершин:
Коэффициенты сжатия:

Растяжение симплекса
Сжатие симплекса в направлении
Новый симплекс с координатами вершин:
Коэффициенты растяжения:

Схема метода Нелдера-Мида
обозначим за ; зададим начальную точку
Находим координаты и вычисляем значение функции во всех вершинах симплекса
Среди вершин симплекса найдем те, что принимают наименьшее, наибольшее и следующее за максимальным значение
Вычислим значение функции в них:
max
min

Схема метода Нелдера-Мида
Выполняем отражение вершины симплекса , вычисляем , получили новый симплекс
Если и
Если но
Если
Растяжение симплекса в направлении
Получаем новую вершину
Если возвращаемся к вычислению 3х вершин симплекса и отражению.
Иначе - данные не используем.
Возвращаемся к вычислению 3х вершин симплекса и отражению.
Сжатие симплекса в направлении
Получаем новую вершину . Если
, , то возвращаемся к вычислению 3х вершин симплекса и отражению.
Иначе – выполняем редукцию к вершине

Условие окончания итераций
- требуемая точность решения
Можно завершать итерации, когда длина максимального из ребер текущего симплекс станет меньше или равна требуемой точности решения
Также можно завершить алгоритм, если выполнено необходимое количество итераций

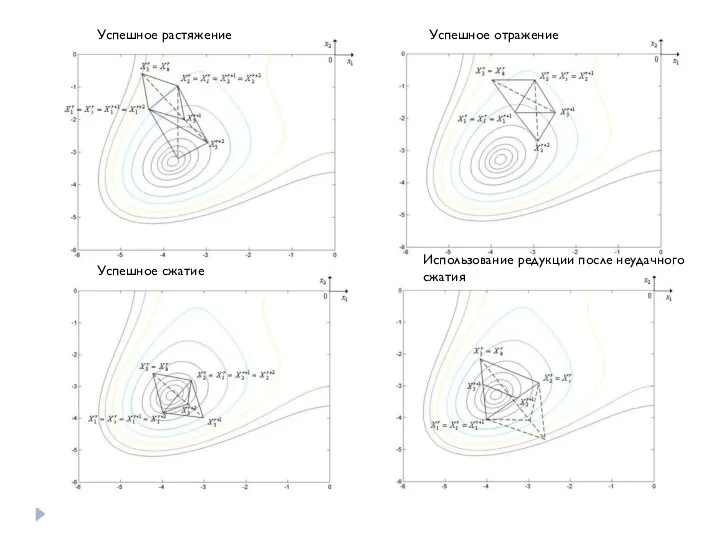
Успешное растяжение
Успешное отражение
Успешное сжатие
Использование редукции после неудачного сжатия

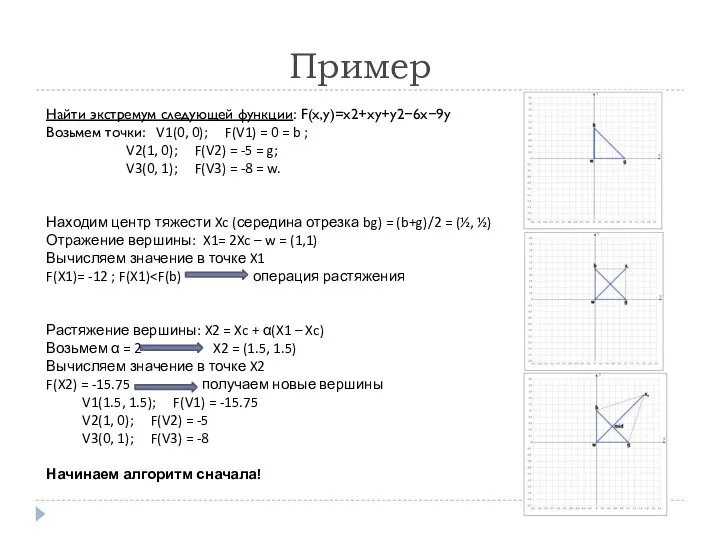
Пример
Найти экстремум следующей функции: F(x,y)=x2+xy+y2−6x−9y
Возьмем точки: V1(0, 0); F(V1) = 0 = b ;
V2(1, 0); F(V2) = -5 = g;
V3(0, 1); F(V3) = -8 = w.
Находим центр тяжести Xc (середина отрезка bg) = (b+g)/2 = (½, ½)
Отражение вершины: X1= 2Xc – w = (1,1)
Вычисляем значение в точке X1
F(X1)= -12 ; F(X1)
Растяжение вершины: X2 = Xc + α(X1 – Xc)
Возьмем α = 2 X2 = (1.5, 1.5)
Вычисляем значение в точке X2
F(X2) = -15.75 получаем новые вершины
V1(1.5, 1.5); F(V1) = -15.75
V2(1, 0); F(V2) = -5
V3(0, 1); F(V3) = -8
Начинаем алгоритм сначала!

Пример
Результат для 10 итераций
Таблица значений для 10 итераций
Ответ:
После 10 итераций мы получаем достаточно точное приближение:
F(0.990, 4.002) = -20.9951
Аналитический экстремум функции достигается в F(1,4) = -21

Визуальный пример работы