Прямые и плоскости в пространстве

Через любые три точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну.
Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
А
В
А
В
С
а
А
α
Аксиомы стереометрии

Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.
Через две пересекающиеся прямые проходит плоскость, и притом только одна.
О
а
в
а
А
Следствия из аксиом стереометрии

а
а
А
а

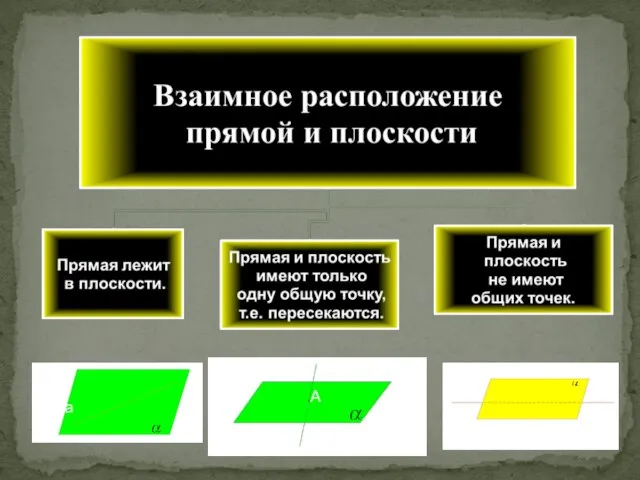
Прямая и плоскость называются параллельными, если они не имеют общих точек.
a
Параллельность прямой и плоскости.

Признак параллельности прямой и плоскости.
Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.

Если плоскость проходит через данную прямую, параллельную другой плоскости, то линия пересечения плоскостей параллельна данной прямой.
Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.
a
a
b
Свойства параллельности прямой и плоскости.

Две плоскости называются параллельными, если они не пересекаются.
Параллельность плоскостей.

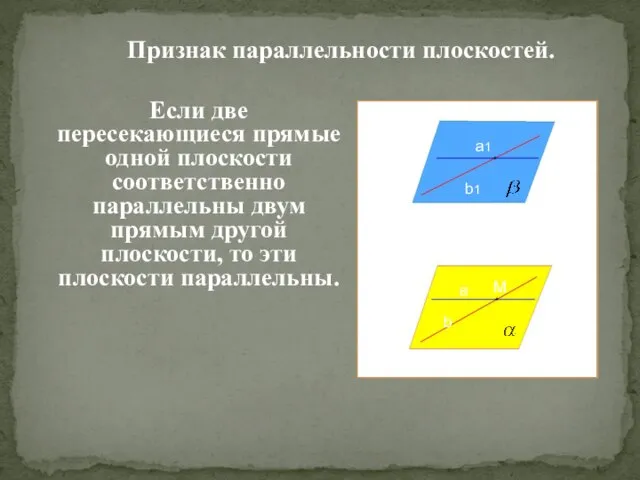
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
a1
b1
а
b
M
Признак параллельности плоскостей.

Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
a
b
Свойства параллельных плоскостей.

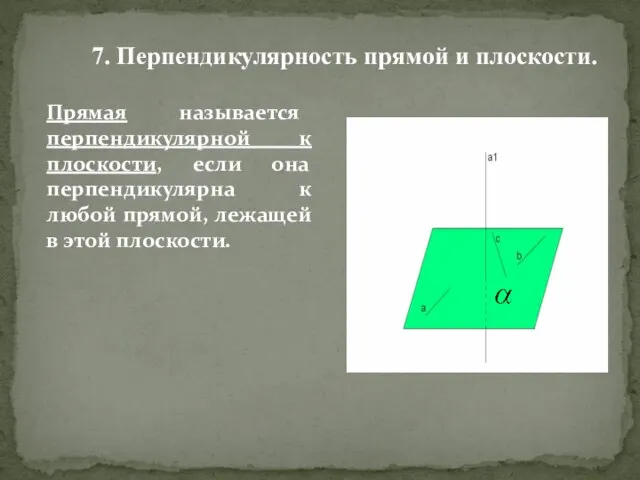
Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.
А
7. Перпендикулярность прямой и плоскости.

1 свойство:
1. Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости.
a
a1
x
Свойства
перпендикулярности прямой и плоскости.

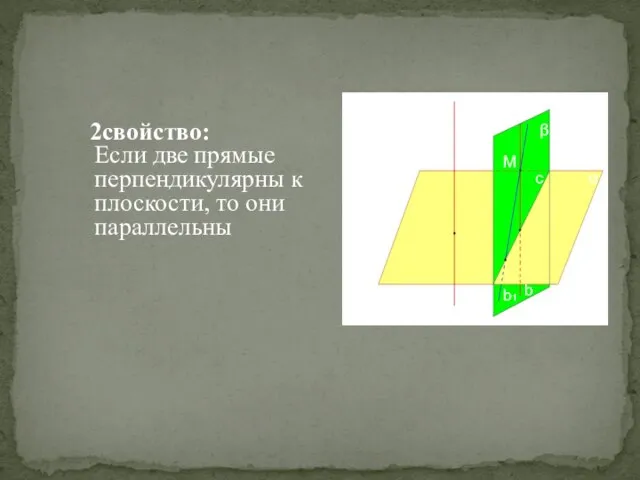
2свойство: Если две прямые перпендикулярны к плоскости, то они параллельны
a
b
b1
c
M
α
β

Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.
a
b
c
Признак
перпендикулярности прямой и плоскости.

Через любую точку пространства проходит прямая, перпендикуляр-ная к данной плоскости, и притом только одна.
O
A
c
Теорема о
перпендикулярности прямой и плоскости.

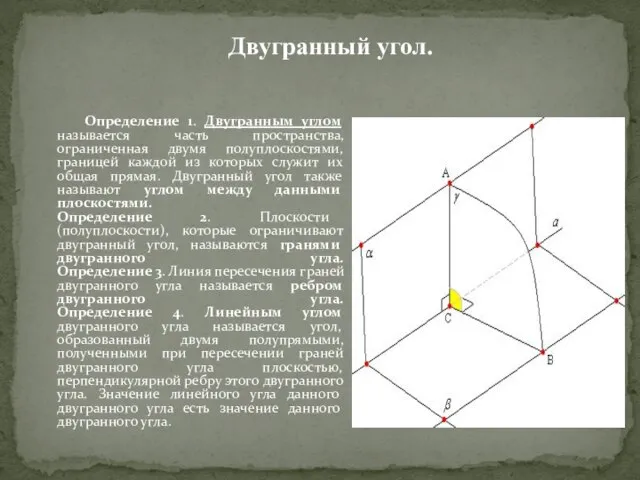
Определение 1. Двугранным углом называется часть пространства, ограниченная двумя полуплоскостями, границей каждой из которых служит их общая прямая. Двугранный угол также называют углом между данными плоскостями.
Определение 2. Плоскости (полуплоскости), которые ограничивают двугранный угол, называются гранями двугранного угла.
Определение 3. Линия пересечения граней двугранного угла называется ребром двугранного угла.
Определение 4. Линейным углом двугранного угла называется угол, образованный двумя полупрямыми, полученными при пересечении граней двугранного угла плоскостью, перпендикулярной ребру этого двугранного угла. Значение линейного угла данного двугранного угла есть значение данного двугранного угла.
Двугранный угол.

Перпендикулярность плоскостей.

Другое изображение перпендикулярных плоскостей:

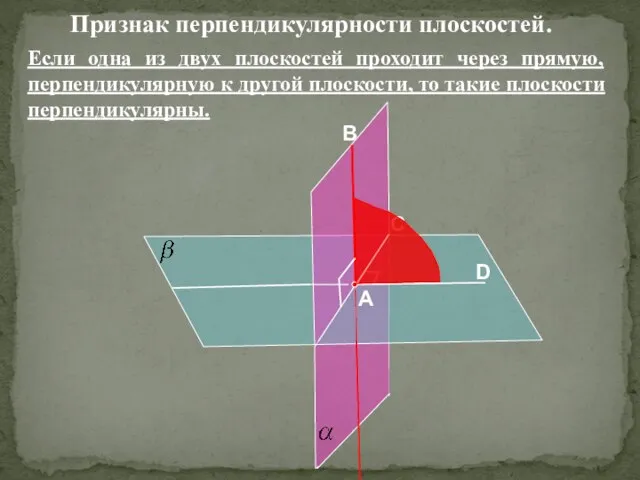
Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.
А
С
Признак перпендикулярности плоскостей.