Построение косинуса

Преобразование графика функции y = cos x
Изменение функции
y = cos x + A
y = k · cos x
y = - cos x
y = ⎜cos x ⎜
Изменение аргумента
y = cos (x – a)
y = cos (k · x)
y = cos (- x)
y = cos ⎢x ⎢

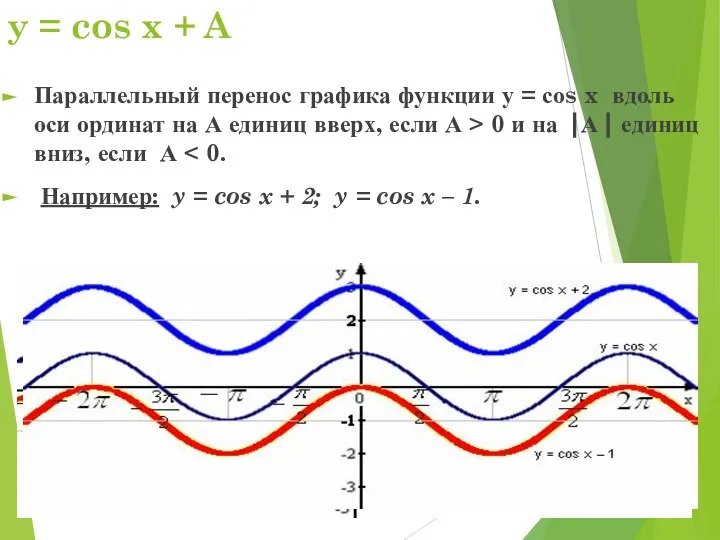
y = cos x + A
Параллельный перенос графика функции у = соs x вдоль оси ординат на А единиц вверх, если А > 0 и на ⎢А ⎢ единиц вниз, если А < 0.
Например: y = cos x + 2; y = cos x – 1.

y = cos x + A (свойства)
Изменяются множество значений функции; наибольшее (наименьшее) значения; нули функции; промежутки положительных (отрицательных) значений.
Например: y = cos x + 2.
E (f): cos x + 2 = a ⇒ cos x = a – 2, т.к. – 1 ≤ y ≤ 1, то –1 ≤ а – 2 ≤ 1 ⇒ 1 ≤ а ≤ 3, т.е. y ∈ [1; 3].
Нули функции: cos x + 2 = 0 ⇒ cos x = -2 данное уравнение не имеет корней т.к. |-2| > 1 ⇒ график данной функции не пересекает ось абсцисс.
f (x) > 0: при любом значении х.
f (x) < 0: нет.
y (наиб) = 3, при: x = 2πn, n ∈ Z (т.к. cos x + 2 = 3 ⇒ cos x = 1 ⇒ x = 2πn, n ∈Z).
y (наим) = 1, при: x = π + 2πn, n ∈Z (т.к. cos x + 2 = 1 ⇒ cos x = - 1 ⇒ x = π + 2πn, n ∈ Z).

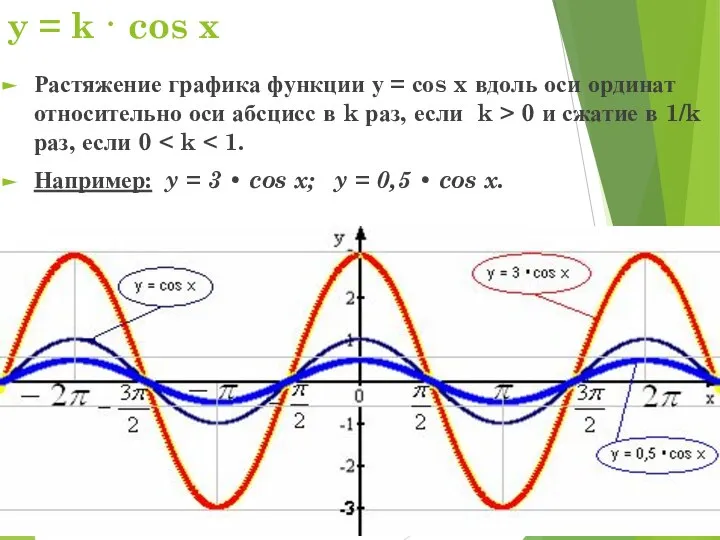
y = k · cos x
Растяжение графика функции у = соs x вдоль оси ординат относительно оси абсцисс в k раз, если k > 0 и сжатие в 1/k раз, если 0 < k < 1.
Например: y = 3 • cos x; y = 0,5 • cos x.

y = k · cos x (свойства)
Изменяется множество значений функции; наибольшее (наименьшее) значения.
Например: y = 3 • cos x
E (f): 3•cos x = a ⇒ cos x = a/3, т.к. – 1 ≤ y ≤ 1, то - 1 ≤ a/3 ≤ 1 ⇒ - 3 ≤ a ≤ 3, т.е. y ∈ [-3; 3].
Функция принимает наибольшее значение, равное 3, при: x = 2πn, n ∈ Z (т.к. 3cos x = 3 ⇒ cos x = 1 ⇒ x = 2πn, n ∈ Z).
Функция принимает наименьшее значение, равное – 3, при: x = π + 2πn, n ∈ Z (т.к. 3cos x = - 3 ⇒ cos x = - 1 ⇒ x = π + 2πn, n ∈ Z).

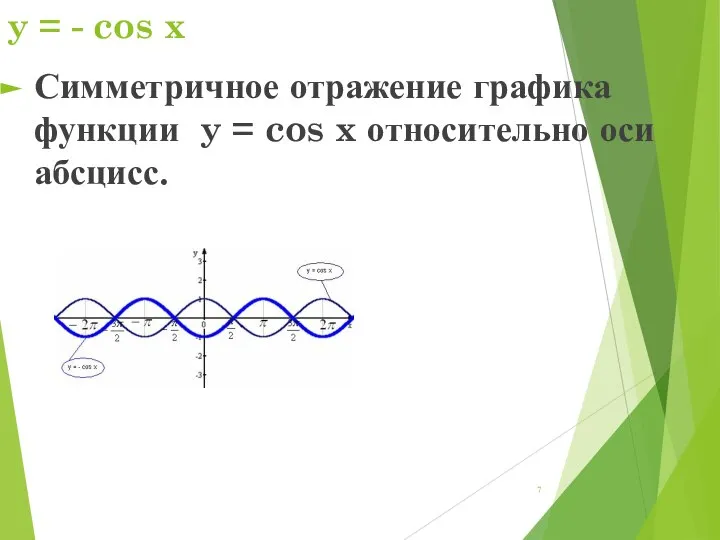
y = - cos x
Симметричное отражение графика функции y = cos x относительно оси абсцисс.

y = - cos x (свойства)
Изменяются промежутки возрастания (убывания); промежутки положительных (отрицательных) значений.
Функция возрастает на отрезке [0; π] и на отрезках, получаемых сдвигами этого отрезка на 2πn, n = ±1, ±2, ±3…
Функция убывает на отрезке [π; 2π] и на отрезках, получаемых сдвигами этого отрезка на 2πn, n = ±1, ±2, ±3…
Функция принимает положительные значения на интервале (π/2; 3π/2) и на интервалах, получаемых сдвигами этого интервала на 2πn, n = ±1, ±2…
Функция принимает отрицательные значения на интервале (- π/2; π/2) и на интервалах, получаемых сдвигами этого интервала на 2πn, n = ±1, ±2…

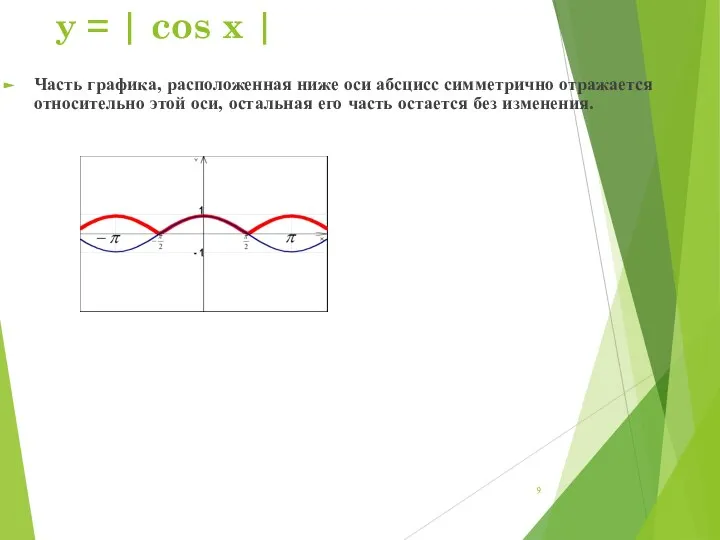
y = | cos x |
Часть графика, расположенная ниже оси абсцисс симметрично отражается относительно этой оси, остальная его часть остается без изменения.

y = |cos x| (свойства)
Изменяются: множество значений функции; период; промежутки возрастания (убывания); наибольшее (наименьшее) значение.
E (f): y ∈[ 0; 1]
Периодичность: Т = π
Функция возрастает на промежутке (π/2; π)+ сдвиги на πn, n∈Z
Функция убывает на промежутке (0; π/2) + сдвиги на πn, n∈Z
f (x) > 0: при любом значении х
f (x) < 0: нет
y (наиб) = 1, при х = 2πn, n∈Z
y (наим) = 0, при х = π/2 + πn, n∈Z

y = cos (x – a)
Параллельный перенос графика функции y = cos x вдоль оси абсцисс на а единиц вправо, если а > 0, на ⎢а ⎢ единиц влево, если а < 0.
Например: y = cos ( x - π/2 ); y = cos ( x +π/4 ).

y = cos (x – a) (свойства)
Изменяются: четность; промежутки возрастания (убывания); нули функции; промежутки положительных (отрицательных) значений.
Например: y = cos (x + π/4)
Четность: f (x) ≠ f (-x) ≠ -f (x), т.к. cos (-(x + π/4)) = cos (-x - π/4)
Функция возрастает на [ 3π/4; 11π/4] + сдвиги на 2πn, n∈Z
Функция убывает на [-π/4; 3π/4 ]+ сдвиги на 2πn, n∈Z
f (x) =0 при х = π/4 +πn, n∈Z
f (x) > 0 при х∈ (-3π/4; π/4) + сдвиги на 2πn, n∈Z
f( (x) <0 при х∈ (π/4; 5π/4) + сдвиги на 2πn, n∈Z

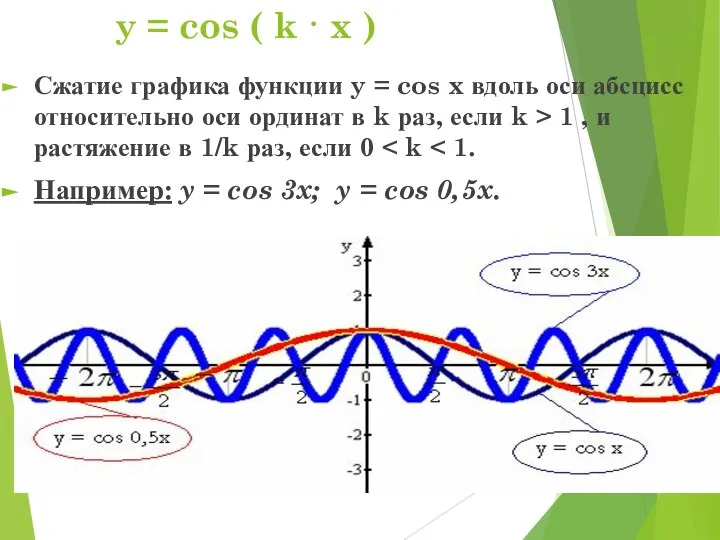
y = cos ( k · x )
Сжатие графика функции y = cos x вдоль оси абсцисс относительно оси ординат в k раз, если k > 1 , и растяжение в 1/k раз, если 0 < k < 1.
Например: y = cos 3x; y = cos 0,5x.

y = cos ( k · x ) (свойства)
Изменяются: период; промежутки возрастания (убывания); нули функции; промежутки положительных (отрицательных) значений.
Например: y = cos 3x
Период: Т = 2π/3, (т.к. наименьший положительный период функции y = cos x равен 2π, то 3Т = 2π ⇒ Т = 2π/3).
Функция возрастает на [π/3; 2π/3] + сдвиги на 2πn/3, n∈Z.
Функция убывает на [0; π/3] + сдвиги на 2πn/3, n∈Z.
f (x) = 0 при х = π/6 + πn/3.
f (x) > 0 при х∈ (-π/6; π/6) + сдвиги на 2πn/3, n ∈ Z.
f (x) < 0 при х∈ (π/6; π/2) + сдвиги на 2πn/3, n ∈ Z.

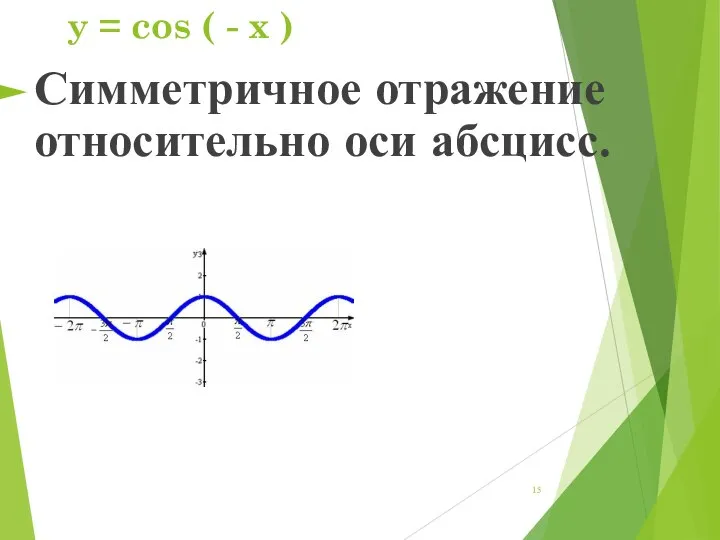
y = cos ( - x )
Симметричное отражение относительно оси абсцисс.

y = cos (-x) (свойства)
В данном случае свойства функции не меняются, так как функция y = cos x – четная и cos (-x) = cos (x) ⇒ все свойства функции y = cos x справедливы и для функции y = cos (-x)

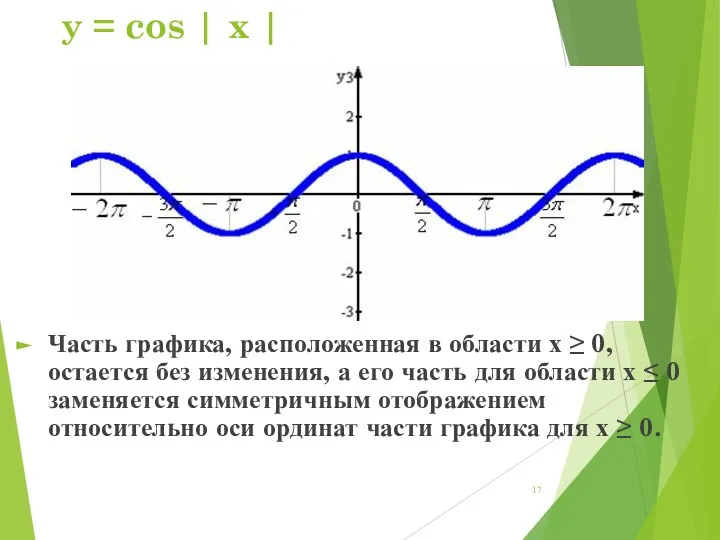
y = cos | x |
Часть графика, расположенная в области х ≥ 0, остается без изменения, а его часть для области х ≤ 0 заменяется симметричным отображением относительно оси ординат части графика для х ≥ 0.

y = cos|x| (свойства)
В данном случае свойства функции не меняются, так как функция y = cos x – четная и cos |x| = cos (-x) = cos (x) ⇒ все свойства функции y = cos x справедливы и для функции y = cos |x|

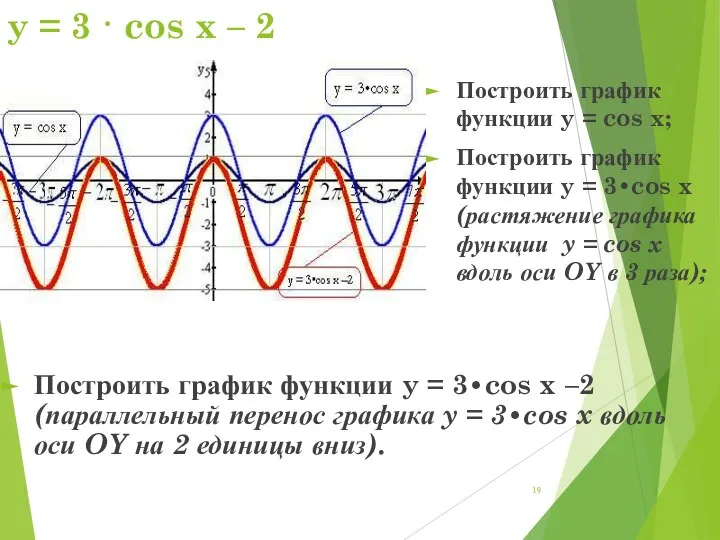
y = 3 · cos x – 2
Построить график функции y = 3•cos x –2 (параллельный перенос графика y = 3•cos x вдоль оси OY на 2 единицы вниз).
Построить график функции y = cos x;
Построить график функции y = 3•cos x (растяжение графика функции y = cos x вдоль оси OY в 3 раза);

Свойства функции y = 3 · cos x – 2
Область определения: D(f): х ∈ R;
Множество значений: y ∈ [- 5; 1], т.к. –1 ≤ cos x ≤ 1 ⇒ - 3 ≤ 3cos x ≤ 3 ⇒ - 5 ≤ 3cos x – 2 ≤ 1;
Периодичность: Т = 2π;
Четность: четная, т.к. 3сos (-x) –2 = 3cos x – 2 ⇒ график функции симметричен относительно оси OY;
Возрастает: на отрезке [π; 2π] и на отрезках, получаемых сдвигами этого отрезка на 2πn, n = ±1, ±2; ±3…;
Убывает: на отрезке [0; π] и на отрезках, получаемых сдвигами этого отрезка на 2πn, n = ±1, ±2, ±3…

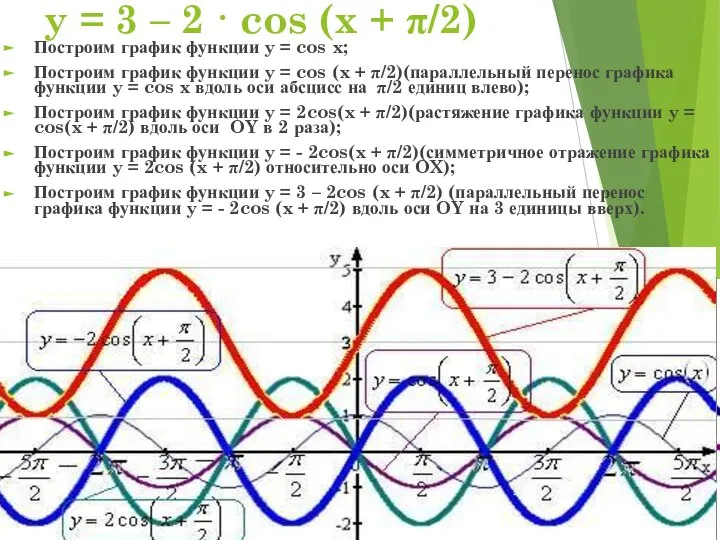
y = 3 – 2 · cos (x + π/2)
Построим график функции y = cos x;
Построим график функции y = cos (x + π/2)(параллельный перенос графика функции y = cos x вдоль оси абсцисс на π/2 единиц влево);
Построим график функции y = 2cos(x + π/2)(растяжение графика функции y = cos(x + π/2) вдоль оси OY в 2 раза);
Построим график функции y = - 2cos(x + π/2)(симметричное отражение графика функции y = 2cos (x + π/2) относительно оси OX);
Построим график функции y = 3 – 2cos (x + π/2) (параллельный перенос графика функции y = - 2cos (x + π/2) вдоль оси OY на 3 единицы вверх).