называется математическое утверждение о свойствах геометрических фигур, требующее доказательства.
2. Через любые две точки проходит прямая.
3. На любом луче от начала можно отложить отрезки, равные данному, причем сколько угодно много.
4.Через точку не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
5. Если две прямые параллельны третьей, то они параллельны между собой.
Вариант 2
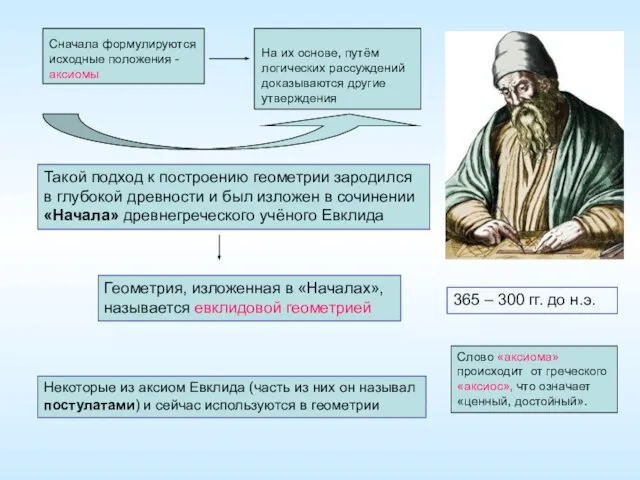
1. Аксиомой называется математическое утверждение о свойствах геометрических фигур, принимаемое без доказательства.
2. Через любые две точки проходит прямая, и притом только одна.
3. Через точку, не лежащую на данной прямой, проходят только две прямые, параллельные данной.
4. Если прямая пересекает одну из двух параллельных прямых, то она перпендикулярна другой прямой.
5. Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.








 Ромб: признаки и свойства
Ромб: признаки и свойства 3
3 Параллелограм и трапеция
Параллелограм и трапеция Прямая пропорциональность и ее график
Прямая пропорциональность и ее график Общие методы решения уравнений
Общие методы решения уравнений Исследование применения математического аппарата сетей Петри для моделирования процесса распределения инцидентов ИТ-службы
Исследование применения математического аппарата сетей Петри для моделирования процесса распределения инцидентов ИТ-службы Компьютерное моделирование процесса подготовки РКН к пуску. Лекция 15
Компьютерное моделирование процесса подготовки РКН к пуску. Лекция 15 Свойства натурального ряда чисел
Свойства натурального ряда чисел Вписанная и описанная окружность. 9 класс
Вписанная и описанная окружность. 9 класс Линейные неравенства
Линейные неравенства Ознакомление с задачей в 2 действия
Ознакомление с задачей в 2 действия Перестановочные тесты и бутстреп анализ
Перестановочные тесты и бутстреп анализ В мире случайных закономерностей. Введение в вероятность. 5 класс
В мире случайных закономерностей. Введение в вероятность. 5 класс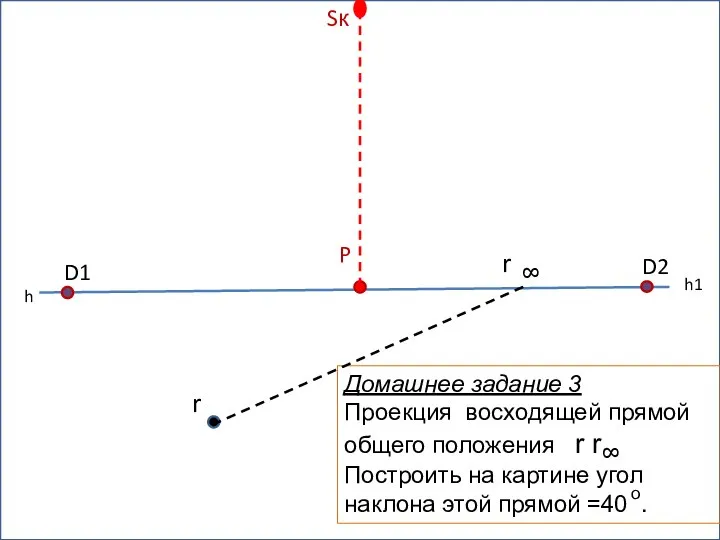 Проекция восходящей прямой общего положения r r
Проекция восходящей прямой общего положения r r Математика вокруг нас. Геометрические узоры и орнамент на посуде
Математика вокруг нас. Геометрические узоры и орнамент на посуде Многочлен и его стандартный вид
Многочлен и его стандартный вид Пересечение высот
Пересечение высот Решение задач по теме Соотношения между сторонами и углами в прямоугольном треугольнике
Решение задач по теме Соотношения между сторонами и углами в прямоугольном треугольнике Презентация на тему Площадь круга и длина окружности
Презентация на тему Площадь круга и длина окружности  Переместительное свойство умножения
Переместительное свойство умножения 797821
797821 Угол. Расстояние
Угол. Расстояние Функция у=arccos x
Функция у=arccos x Площадь криволинейной трапеции
Площадь криволинейной трапеции Ãkom Erikom do 100
Ãkom Erikom do 100 Подготовка к ЕГЭ (профильный уровень). Теория вероятности
Подготовка к ЕГЭ (профильный уровень). Теория вероятности Диагностика и развитие мышления школьников на уроках математики
Диагностика и развитие мышления школьников на уроках математики Сложение чисел. Как можно найти значение суммы 7 + 7
Сложение чисел. Как можно найти значение суммы 7 + 7