Слайд 21. Сравнение бесконечно малых.
Две б.м.ф. сравниваются между собой с помощью их отношения.

Слайд 32. Основные теоремы об эквивалентных б.м.ф.
Теорема 1: Предел отношения двух бесконечно малых

функций не изменится, если каждую или одну их них заменить эквивалентной ей бесконечно малой.
Теорема 2: Разность двух эквивалентных бесконечно малых функций есть бесконечно малая более высокого порядка, чем каждая из них
Теорема 3: Сумма конечного числа бесконечно малых функций разных порядков эквивалентна слагаемому низшего порядка
Слагаемое, эквивалентное сумме бесконечно малых функций, называется главной частью этой суммы.
Замена суммы бесконечно малых функций ее главной частью называется отбрасыванием бесконечно малых высшего порядка.
Слайд 43. Применение эквивалентных бесконечно малых функций.

Слайд 53. Применение эквивалентных бесконечно малых функций.
Приближенные вычисления
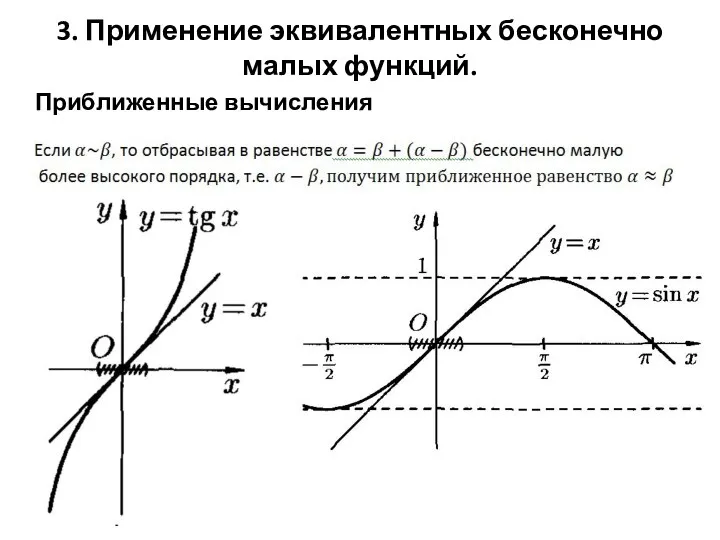
Слайд 63. Применение эквивалентных бесконечно малых функций.
Приближенные вычисления
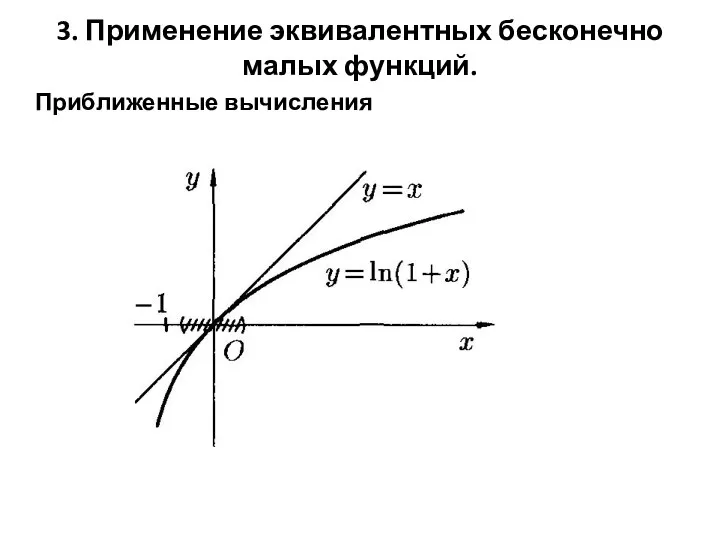
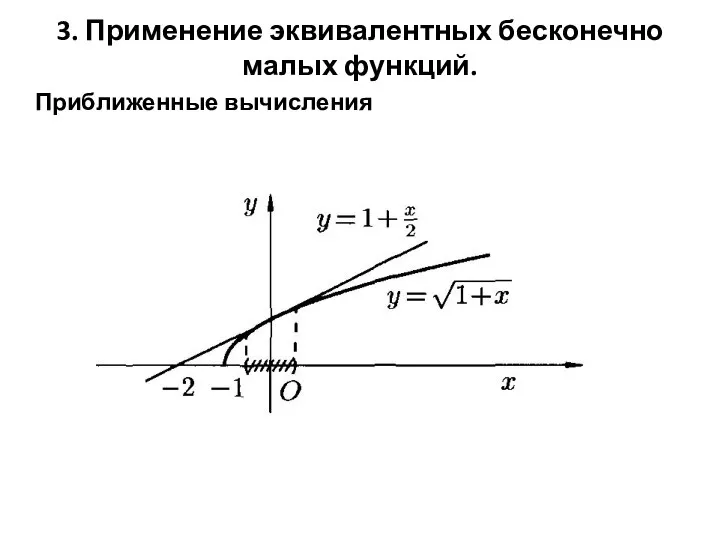
Слайд 73. Применение эквивалентных бесконечно малых функций.
Приближенные вычисления






 Раз, два, три. Спортивно-математический турнир
Раз, два, три. Спортивно-математический турнир Графики степенных функций
Графики степенных функций Prezentatsia_2
Prezentatsia_2 Число и цифра 1. Часть 1
Число и цифра 1. Часть 1 Математическое моделирование многокомпонентной ректификации. Коммерческие симуляторы
Математическое моделирование многокомпонентной ректификации. Коммерческие симуляторы Дробно-рациональные уравнения
Дробно-рациональные уравнения Презентация на тему Функция. График функции.
Презентация на тему Функция. График функции.  Теорема Виета. Урок систематизации, обобщения и контроля знаний
Теорема Виета. Урок систематизации, обобщения и контроля знаний Внеурочная деятельность по математике, 3 класс
Внеурочная деятельность по математике, 3 класс Функция
Функция Прямоугольный параллелепипед
Прямоугольный параллелепипед Устный счет. Умножение положительных и отрицательных чисел
Устный счет. Умножение положительных и отрицательных чисел Равенство векторов
Равенство векторов Вероятность
Вероятность Необычная раскраска по математике
Необычная раскраска по математике Сказка об отрезке
Сказка об отрезке Математические ребусы
Математические ребусы Дополнительные построения в трапеции при решении задач
Дополнительные построения в трапеции при решении задач Вычислите логарифм. Практическая работа
Вычислите логарифм. Практическая работа Решение задач с помощью дифференциальных уравнений
Решение задач с помощью дифференциальных уравнений Дробная схватка
Дробная схватка Презентация на тему Отрезок. Графики
Презентация на тему Отрезок. Графики  Перпендикулярность прямой и плоскости (10 класс)
Перпендикулярность прямой и плоскости (10 класс) Признаки равенства треугольников
Признаки равенства треугольников Вычисление неопределенного интеграла
Вычисление неопределенного интеграла Презентация на тему Уравнение касательной
Презентация на тему Уравнение касательной  Игра 7
Игра 7 Разложение многочлена на множители способом группировки. 7 класс
Разложение многочлена на множители способом группировки. 7 класс