Содержание
- 2. Тема урока
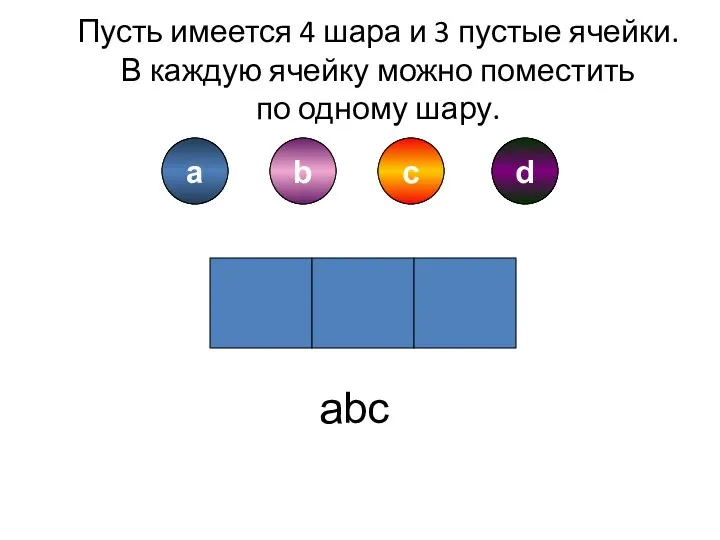
- 3. Пусть имеется 4 шара и 3 пустые ячейки. В каждую ячейку можно поместить по одному шару.
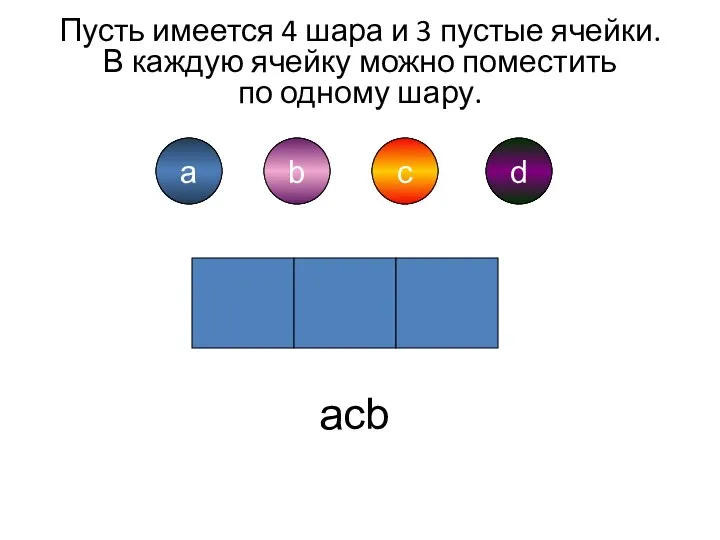
- 4. a b d c a b c d acb Пусть имеется 4 шара и 3 пустые
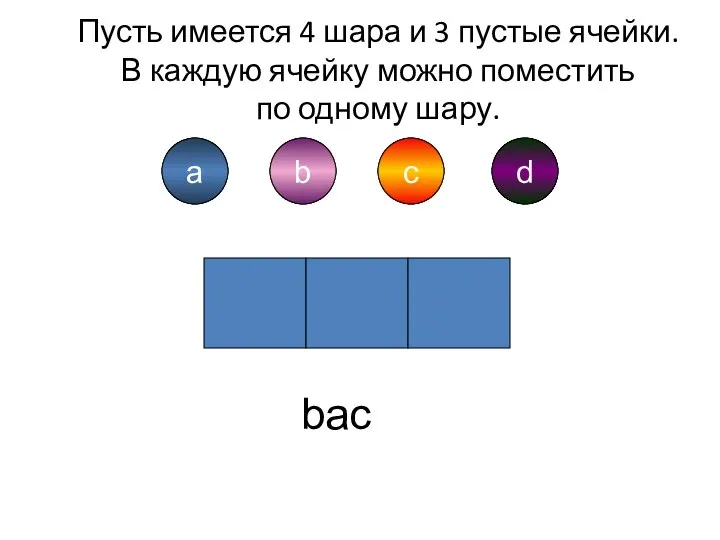
- 5. a b d c a b c d bac Пусть имеется 4 шара и 3 пустые
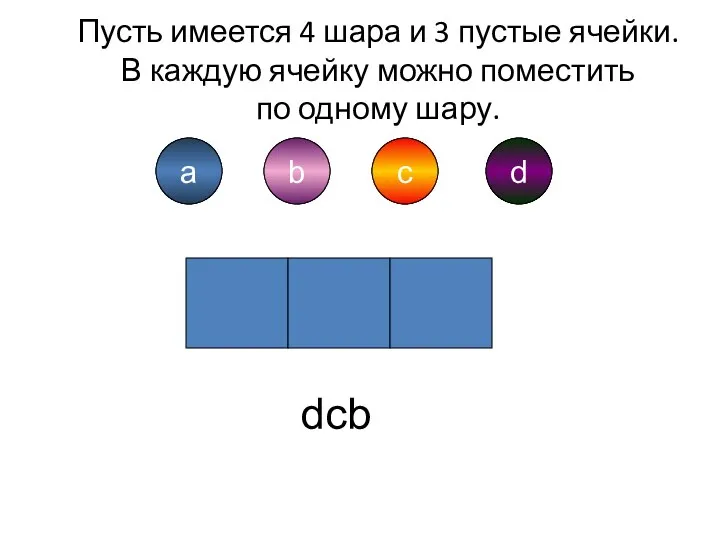
- 6. a b d c a b c d dcb Пусть имеется 4 шара и 3 пустые
- 7. Определение Размещением из n элементов по k (k ≤ n) называется любое множество, состоящее из k
- 8. Обозначение:
- 9. Все возможные размещения по 3 элемента из 4: abc, abd, acb, acd, adb, adc, bac, bad,
- 10. Первый элемент можно выбрать 4-мя способами. Для каждого выбранного первого элемента второй можно выбрать из оставшихся
- 11. Формула размещения для k Формула размещения для k = n
- 12. Пример 1 Учащиеся 2 класса изучают 9 предметов. Сколькими способами можно составить расписание на один день,
- 13. Пример 2 Сколько трехзначных чисел (без повторения цифр в записи числа) можно составить из цифр 0,
- 14. Решение задач № 754 Сколькими способами может разместиться семья из трех человек в четырехместном купе, если
- 15. Решение задач № 757 Сколькими способами тренер может определить, кто из 12 спортсменок, готовых к участию
- 16. Задачи на закрепление Сколькими способами могут быть заняты первое, второе и третье места (по одному человеку
- 18. Скачать презентацию





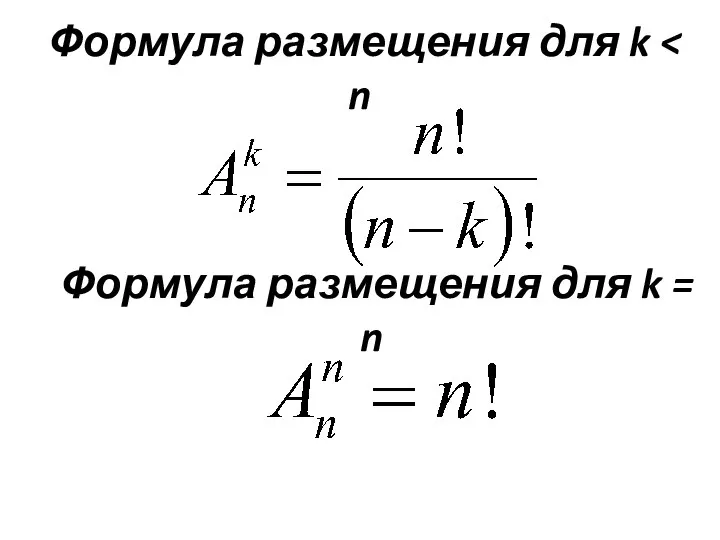





 Случаи вычитания 11 -
Случаи вычитания 11 - Статистические графики
Статистические графики математика гр 32 парність-2.docx
математика гр 32 парність-2.docx Число та цифра 6
Число та цифра 6 Конус. Виды конусов. Конусы в нашей жизни
Конус. Виды конусов. Конусы в нашей жизни Сечения в многогранниках
Сечения в многогранниках Уравнение линии на плоскости. Уравнение фигуры. Уравнение окружности
Уравнение линии на плоскости. Уравнение фигуры. Уравнение окружности Решение задач с помощью уравнений
Решение задач с помощью уравнений Решение задач на движение
Решение задач на движение Понятие спирали
Понятие спирали Геометрические построения
Геометрические построения Элементы теории вероятностей
Элементы теории вероятностей Проценты
Проценты Математические ребусы
Математические ребусы Площади. ОГЭ
Площади. ОГЭ Средняя линия треугольника (8 класс)
Средняя линия треугольника (8 класс) Текстовые задачи на движение по прямой
Текстовые задачи на движение по прямой Основное свойство дроби
Основное свойство дроби Две задачи на дроби
Две задачи на дроби Статистические гипотезы
Статистические гипотезы Собираем ягоды. Математика 1 класс. Итоговое повторение. Тренажёр
Собираем ягоды. Математика 1 класс. Итоговое повторение. Тренажёр Конструктивные объекты
Конструктивные объекты Математика: психология и нейронауки. Чем нейробиология и когнитивная психология могут помочь учителю математики?
Математика: психология и нейронауки. Чем нейробиология и когнитивная психология могут помочь учителю математики? Презентация по математике "Что такое понятие" -
Презентация по математике "Что такое понятие" -  Параллельность плоскостей
Параллельность плоскостей Экономический биатлон. “Экономика и математика”. Финал
Экономический биатлон. “Экономика и математика”. Финал Методичні основи ознайомлення здобувачів освіти з діями множення і ділення, зв'язком між ними
Методичні основи ознайомлення здобувачів освіти з діями множення і ділення, зв'язком між ними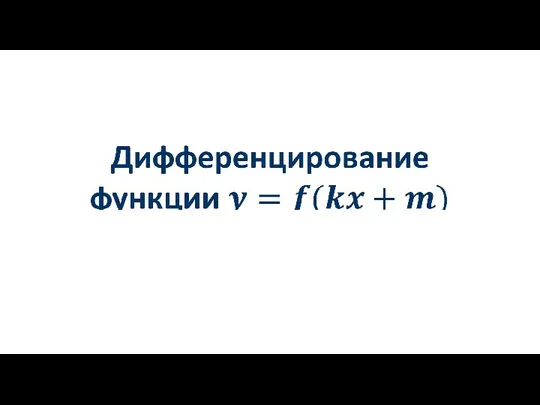 Дифференцирование функции y=f(kx+m)
Дифференцирование функции y=f(kx+m)