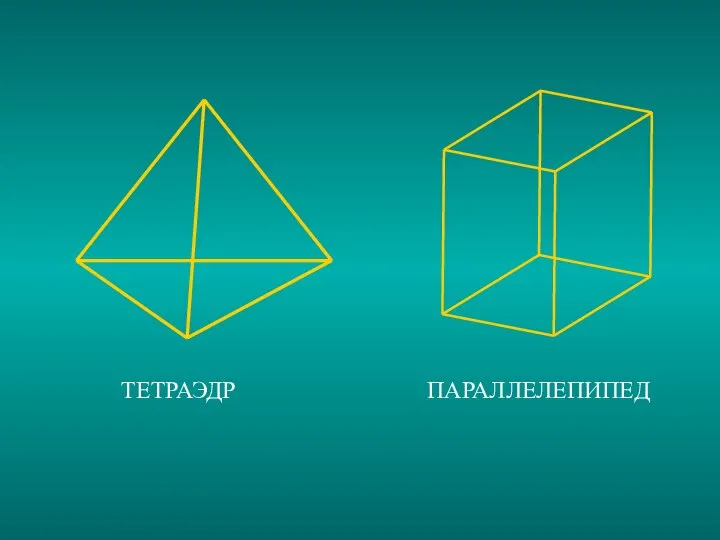
Слайд 2Многогранники
Понятие многогранника. Призма.

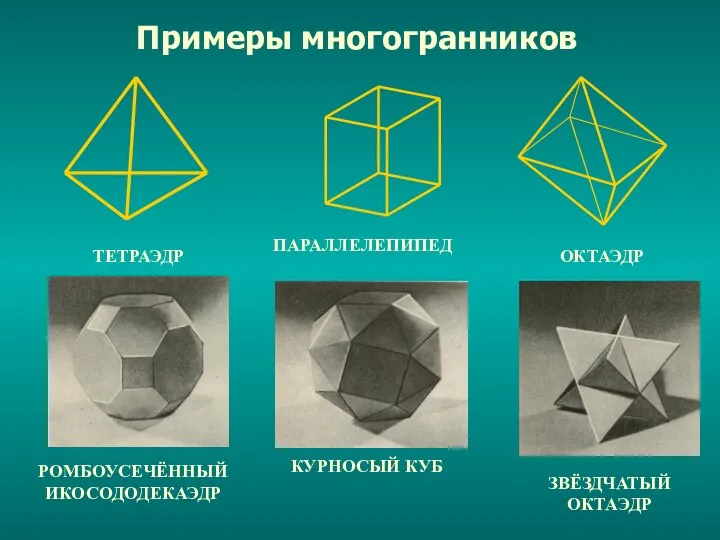
Слайд 4Поверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело, будем называть многогранной

поверхностью или
многогранником
Слайд 6Грани многогранника – многоугольники, из которых составлен многогранник.
Ребра многогранника – стороны граней.
Вершины

многогранника – концы рёбер.
Диагональ многогранника – отрезок, соединяющий две вершины, не принадлежащие одной грани.
Секущая плоскость – плоскость, по обе стороны от которой имеются точки многогранника.
Сечение многогранника – общая часть многогранника и секущей плоскости.
Слайд 7Выпуклые и невыпуклые многогранники
Выпуклый многогранник
Невыпуклый многогранник
Многогранник называется выпуклым, если он расположен по
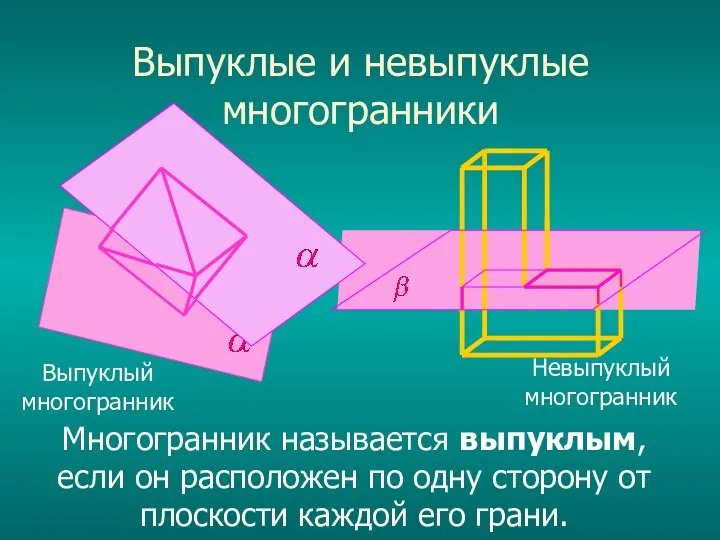
одну сторону от плоскости каждой его грани.
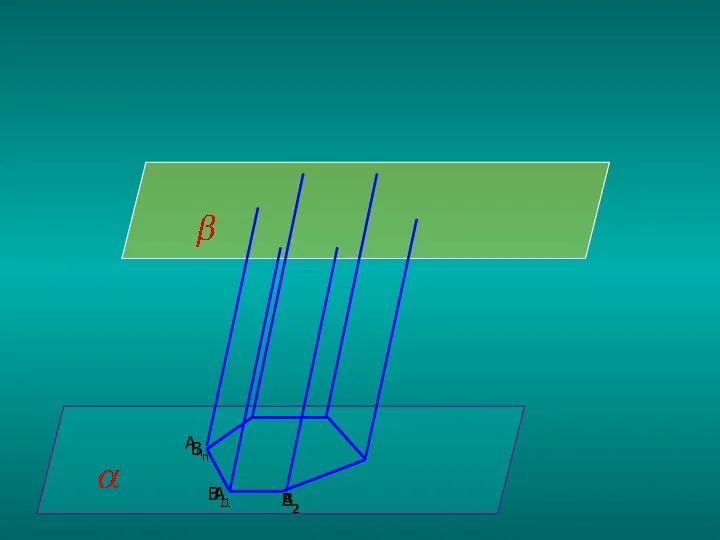
Слайд 9Призма – это многогранник, составленный из двух равных многоугольников А1А2…Аn и В1В2…Вn

, расположенных в параллельных плоскостях, и n параллелограммов.
Многоугольники А1А2…Аn и В1В2…Вn называются основаниями, а параллелограммы – боковыми гранями призмы. Отрезки А1В1, А2В2, …, АnВn называются боковыми ребрами призмы.
Призму с основаниями А1А2…Аn и В1В2…Вn обозначают А1А2…АnВ1В2…Вn и называют n-угольной призмой.
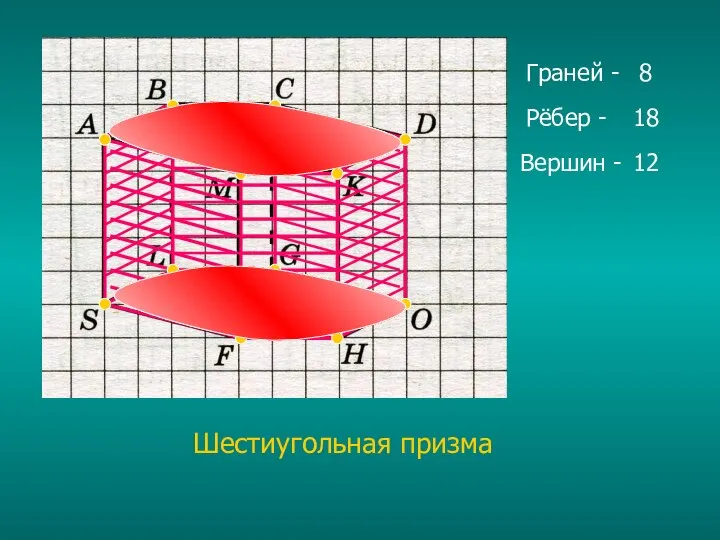
Слайд 10Граней -
Вершин -
Рёбер -
8
12
18
Шестиугольная призма
Слайд 11Перпендикуляр, проведённый из какой-нибудь точки одного основания к плоскости другого основания, называется
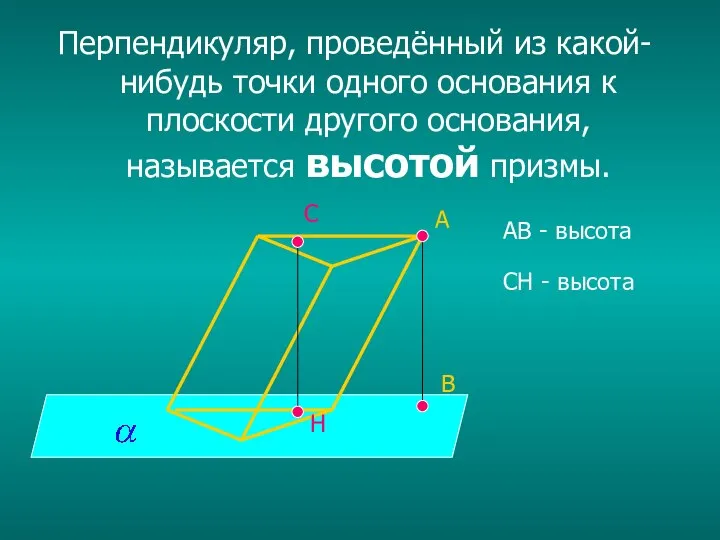
высотой призмы.
А
АВ - высота
СН - высота
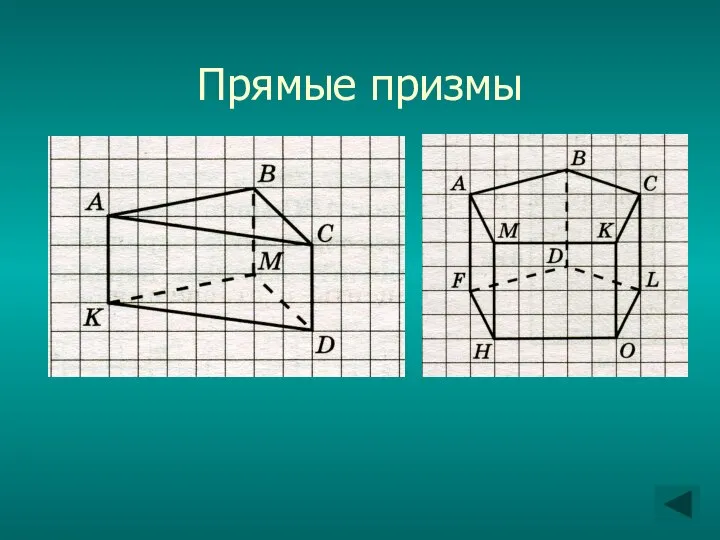
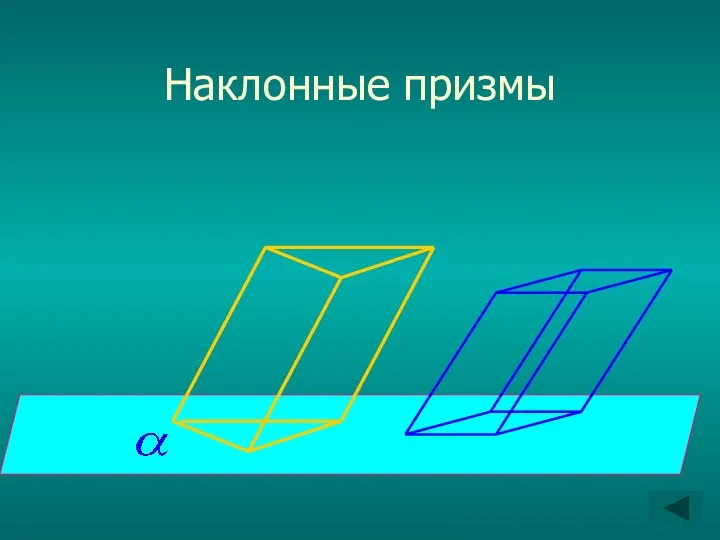
Слайд 12Если боковые рёбра призмы перпендикулярны к основаниям, то призма называется прямой, в

противном случае наклонной.
Высота прямой призмы равна её боковому ребру.
Прямая призма называется правильной, если её основания – правильные многоугольники. У такой призмы все боковые грани – равные прямоугольники.
Слайд 13Призмы
прямые
наклонные
правильные









 Презентация на тему Формулы сокращённого умножения
Презентация на тему Формулы сокращённого умножения  тринометрические функции
тринометрические функции Деление одночлена на одночлен
Деление одночлена на одночлен Теоремы сложения и умножения вероятностей
Теоремы сложения и умножения вероятностей Двоичная арифметика
Двоичная арифметика Презентация на тему Умножение суммы на число
Презентация на тему Умножение суммы на число  Обучение решению задач на движение при обобщающем повторении
Обучение решению задач на движение при обобщающем повторении Обчислення площі прямокутника, розв'язування задач, пов'язаних із площею прямокутника. 4 клас
Обчислення площі прямокутника, розв'язування задач, пов'язаних із площею прямокутника. 4 клас Область визначення функції
Область визначення функції Презентация на тему Тренажер по формулам сокращенного умножения
Презентация на тему Тренажер по формулам сокращенного умножения  Презентация на тему ПРОИЗВОДНАЯ СТЕПЕННОЙ ФУНКЦИИ
Презентация на тему ПРОИЗВОДНАЯ СТЕПЕННОЙ ФУНКЦИИ  Таблицы, часть 1, 5-9 классы
Таблицы, часть 1, 5-9 классы Predel_funktsii_v_tochke
Predel_funktsii_v_tochke Цилиндр, конус, шар. Решение задач
Цилиндр, конус, шар. Решение задач Название круглых сотен
Название круглых сотен Треугольник и его виды
Треугольник и его виды Классическое определение вероятности
Классическое определение вероятности Множества и операции над ними
Множества и операции над ними Reshenie_zadach_1
Reshenie_zadach_1 Площадь параллелограмма
Площадь параллелограмма Десятичные дроби. Тест
Десятичные дроби. Тест Система географических координат
Система географических координат Интерактивная игра-тренажёр. Считаем с Лунтиком (2 класс). Умножение и деление на 5
Интерактивная игра-тренажёр. Считаем с Лунтиком (2 класс). Умножение и деление на 5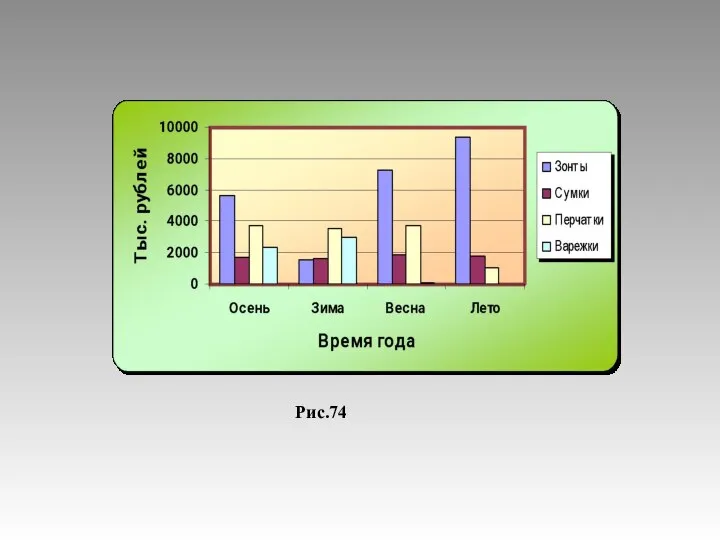 Диаграммы. Фронтальная работа. 6 класс
Диаграммы. Фронтальная работа. 6 класс неопред интеграл
неопред интеграл Презентация на тему Математический КВН
Презентация на тему Математический КВН  Математическое моделирование. Основные положения
Математическое моделирование. Основные положения Математический диктант №2. Геометрия 7класс. Первый признак равенства треугольников
Математический диктант №2. Геометрия 7класс. Первый признак равенства треугольников