Содержание
- 2. Определение Показательная функция – это функция вида , где x – переменная, - заданное число, >0,
- 3. Область определения показательной функции: D (y)=R – множество всех действительных чисел. Область значений показательной функции: E
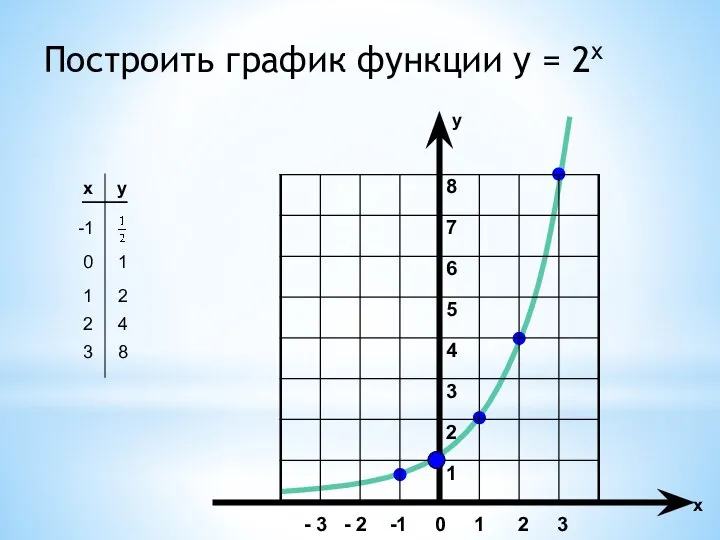
- 4. Построить график функции y = 2x x y -1 8 7 6 5 4 3 2
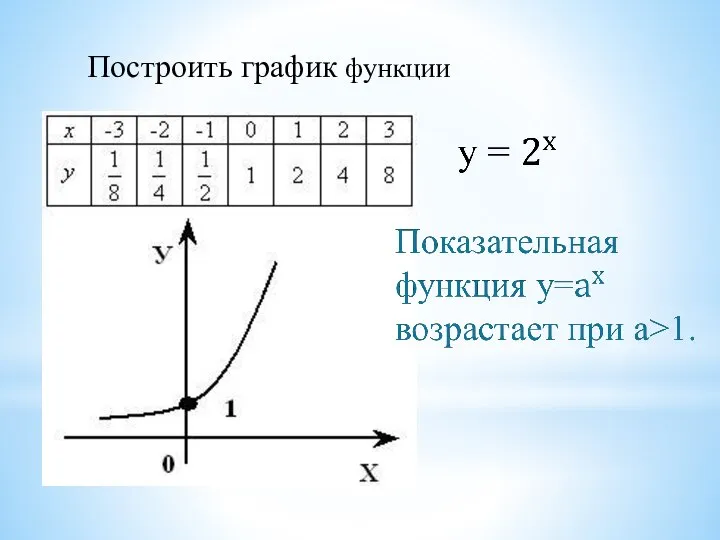
- 5. Построить график функции
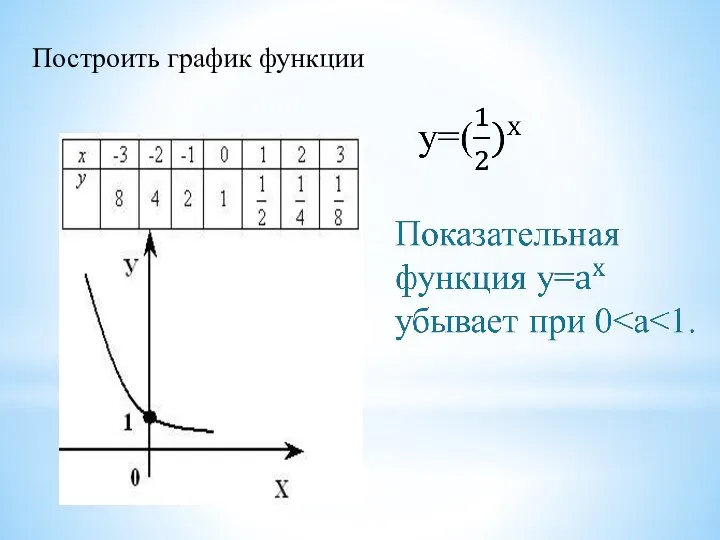
- 6. Построить график функции
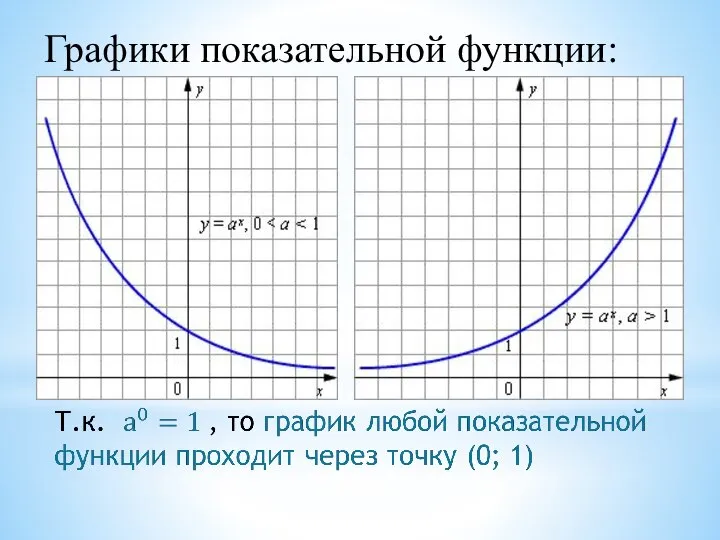
- 7. Графики показательной функции:
- 8. Показательная функция обладает следующими свойствами: D(f): множество R всех действительных чисел; E(f): множество всех положительных чисел;
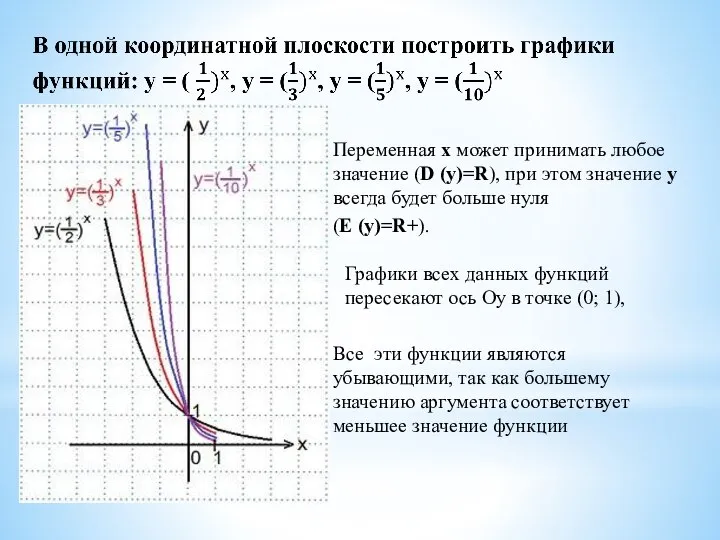
- 9. Переменная х может принимать любое значение (D (y)=R), при этом значение у всегда будет больше нуля
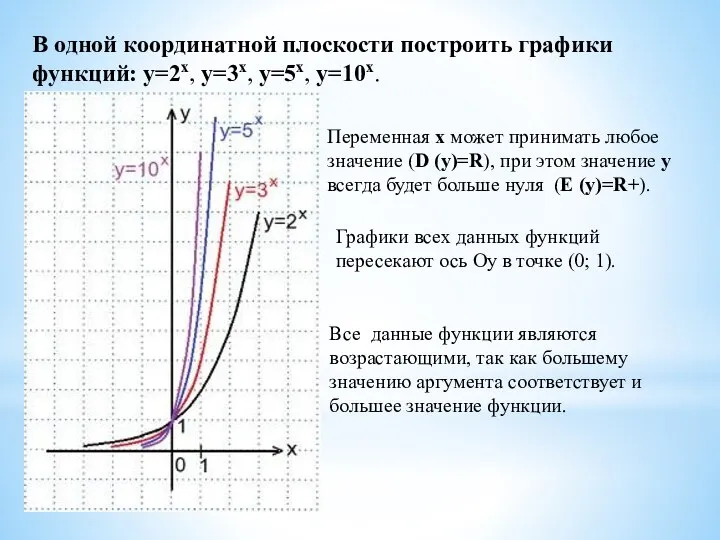
- 10. В одной координатной плоскости построить графики функций: y=2x, y=3x, y=5x, y=10x. Переменная х может принимать любое
- 12. Показательная функция Сравнение чисел с использованием свойств показательной функции Сравнение числа с 1 а) аналитический способ;
- 13. Задача 1 Сравнить числа Решение Ответ:
- 14. Задача 2 Сравнить число с 1. Решение -5 Ответ:
- 15. Задача 3 Cравнить число р с 1 р = 2 > 1, то функция у =
- 16. Используя свойства возрастания и убывания показательной функции сравнить числа: Сравнить: а) 53 и 55; б) 47
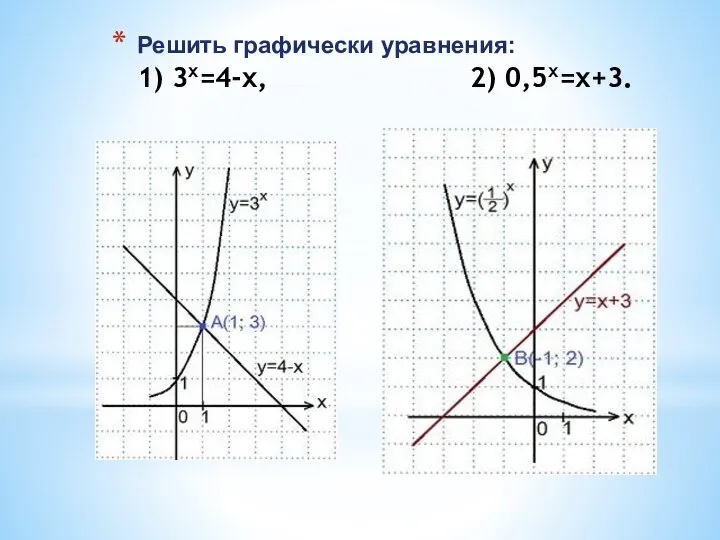
- 17. Решить графически уравнения: 1) 3x=4-x, 2) 0,5х=х+3.
- 18. Давление воздуха убывает с высотой по закону: P- давление на высоте h, P0 - давление на
- 19. Рост народонаселения Изменение числа людей в стране на небольшом отрезке времени описывается формулой , где N0
- 20. Закон органического размножения: при благоприятных условиях (отсутствие врагов, большое количество пищи) живые организмы размножались бы по
- 22. Скачать презентацию












 Логическая задача. Способы решения
Логическая задача. Способы решения Множество и его элементы
Множество и его элементы Применение производной при решении задач ЕГЭ. 11 класс
Применение производной при решении задач ЕГЭ. 11 класс Доминино
Доминино Организация работы учителя с обучающимися, испытывающими трудности в обучении математике на уровне основного общего образования
Организация работы учителя с обучающимися, испытывающими трудности в обучении математике на уровне основного общего образования Неравенство треугольника
Неравенство треугольника Сумма углов треугольника
Сумма углов треугольника Второй признак подобия треугольников
Второй признак подобия треугольников Классическое определение вероятности
Классическое определение вероятности Методы решения систем уравнения
Методы решения систем уравнения Числа от 1 до 1000, умножение и деление. Приемы устных вычислений
Числа от 1 до 1000, умножение и деление. Приемы устных вычислений Понятие о комплексных числах. Рациональные функции одной переменной. Лекция 14
Понятие о комплексных числах. Рациональные функции одной переменной. Лекция 14 Действительные числа
Действительные числа Презентация на тему Решение систем уравнений
Презентация на тему Решение систем уравнений  Производная степенной функции
Производная степенной функции Интегралы от тригонометрических функций
Интегралы от тригонометрических функций Произведение многочленов
Произведение многочленов Теорема Пифагора. Деление дробей
Теорема Пифагора. Деление дробей Домашняя работа по математике
Домашняя работа по математике Свойства логарифмов
Свойства логарифмов Показательная функция. Построение и преобразование графика функции
Показательная функция. Построение и преобразование графика функции Презентация на тему Метод интервалов
Презентация на тему Метод интервалов  Задачи на нахождение неизвестного
Задачи на нахождение неизвестного Онлайн-тестирование по математике
Онлайн-тестирование по математике Математический КВН
Математический КВН Основы теории MOM метода. Настройка параметров EM симулятора на основе метода MOM
Основы теории MOM метода. Настройка параметров EM симулятора на основе метода MOM Великие математики
Великие математики Аттестационная работа: Образовательная программа элективного курса Правильные многогранники
Аттестационная работа: Образовательная программа элективного курса Правильные многогранники