- Главная
- Математика
- Презентация на тему Вклад Пифагора в развитие музыки 7 класс

Содержание
- 2. В Древней Греции была впервые замечена некая закономерная связь между звуками и математическими величинами. Открытие этих
- 3. Главный вклад Пифагора в развитие музыки заключался в учении о пропорциях звуков. За основу были взяты
- 4. АФОРИЗМЫ И ЦИТАТЫ О МАТЕМАТИКЕ
- 5. ХУГО ШТЕЙНГАУС
- 7. Математик уже кое-что может, но, разумеется, не то, что от него хотят получить в данный момент.
- 10. БЕРТРАН РАССЕЛ
- 13. ИОГАНН ВОЛЬФГАНГ ГЕТЕ
- 18. Скачать презентацию
Слайд 2 В Древней Греции была впервые замечена некая закономерная связь между звуками
В Древней Греции была впервые замечена некая закономерная связь между звуками

и математическими величинами. Открытие этих закономерностей связано с именем Пифагора. Согласно его теории, музыка представляла собой некую физическую материю. С помощью анализа соотношений между различными сонорными повышениями были определены основные типы гамм, что позволило упорядочить всю систему музыкальной гармонии на Востоке.
Большое влияние на теорию Пифагора оказали астрономы и математики Вавилона, Основываясь на их трудах, он создал космическую теорию, которая представила мир как некое пространство гармонии, в которой планеты излучали непрерывные звуки, упорядоченные аналогично нотам в гамме.
Согласно этой теории, низкие звуки соответствовали Луне, высокие - планете Земля и т.д. Пифагор отмечал также, что количество нот в гамме соответствует количеству планет на небе - и равняется магической цифре 7.
Большое влияние на теорию Пифагора оказали астрономы и математики Вавилона, Основываясь на их трудах, он создал космическую теорию, которая представила мир как некое пространство гармонии, в которой планеты излучали непрерывные звуки, упорядоченные аналогично нотам в гамме.
Согласно этой теории, низкие звуки соответствовали Луне, высокие - планете Земля и т.д. Пифагор отмечал также, что количество нот в гамме соответствует количеству планет на небе - и равняется магической цифре 7.
Слайд 3Главный вклад Пифагора в развитие музыки заключался в учении о пропорциях звуков.
Главный вклад Пифагора в развитие музыки заключался в учении о пропорциях звуков.

За основу были взяты струнные инструменты, представлявшие собой доску с натянутыми струнами. В результате многочисленных опытов были найдены определенные числовые выражения (интервальные коэффициенты) - октава (2/1), квинта (3/2) и кварта (4/3). Отсчитывая последовательно квинты от исходного звука и перенося их в одну октаву, можно было получить числовое значение любого звука диатонической или хроматической гаммы.
Дальнейшее развитие музыкальная теория нашла в трудах Никомаха, К. Птолемея (I-II вв. н. э.). Этическую концепцию музыки развивали Платон, Аристотель и др. философы.
ПИФАГОР
Слайд 4АФОРИЗМЫ И
ЦИТАТЫ
О МАТЕМАТИКЕ
АФОРИЗМЫ И
ЦИТАТЫ
О МАТЕМАТИКЕ

Слайд 5ХУГО ШТЕЙНГАУС
ХУГО ШТЕЙНГАУС

Слайд 7Математик уже кое-что может, но, разумеется, не то, что от него хотят
Математик уже кое-что может, но, разумеется, не то, что от него хотят

получить в данный момент.
С тех пор как за теорию относительности принялись математики, я ее уже сам больше не понимаю.
Существует поразительная возможность овладеть предметом математически, не поняв существа дела.
Законы математики, имеющие какое-либо отношение к реальному миру, ненадежны; а надежные математические законы не имеют отношения к реальному миру.
АЛЬБЕРТ ЭЙНШТЕЙН
С тех пор как за теорию относительности принялись математики, я ее уже сам больше не понимаю.
Существует поразительная возможность овладеть предметом математически, не поняв существа дела.
Законы математики, имеющие какое-либо отношение к реальному миру, ненадежны; а надежные математические законы не имеют отношения к реальному миру.
АЛЬБЕРТ ЭЙНШТЕЙН
Слайд 10БЕРТРАН РАССЕЛ
БЕРТРАН РАССЕЛ

Слайд 13ИОГАНН ВОЛЬФГАНГ ГЕТЕ
ИОГАНН ВОЛЬФГАНГ ГЕТЕ









 Десятичные дроби по-английски. Бинарный урок
Десятичные дроби по-английски. Бинарный урок Формулы сокращенного умножения. Формулы суммы и разности кубов двух выражений (изучение нового материала)
Формулы сокращенного умножения. Формулы суммы и разности кубов двух выражений (изучение нового материала) Условная минимизация. Прямые методы решения задачи условной минимизации
Условная минимизация. Прямые методы решения задачи условной минимизации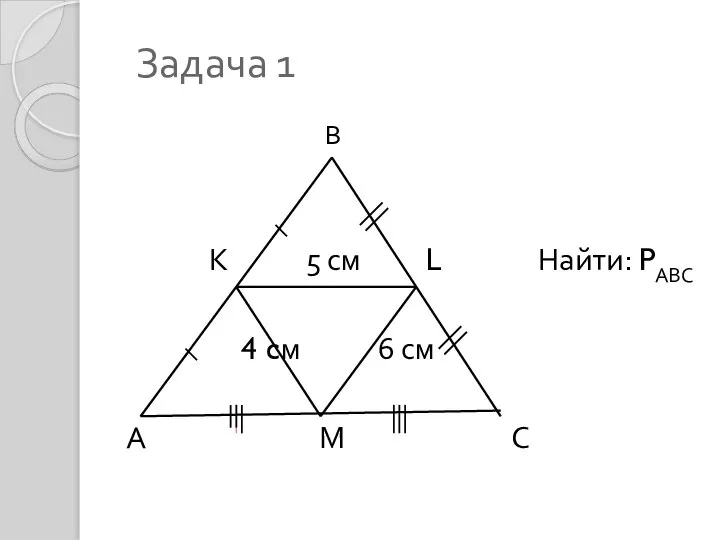 Средняя линия треугольника
Средняя линия треугольника Число и цифра 1. 1 класс
Число и цифра 1. 1 класс Показательные уравнения
Показательные уравнения Все действия с десятичными дробями
Все действия с десятичными дробями Координаты вектора. Простейшие задачи в координатах
Координаты вектора. Простейшие задачи в координатах Вероятность равновозможных событий
Вероятность равновозможных событий Равносильные формулы. Уроки 17-18
Равносильные формулы. Уроки 17-18 Цилиндр. 4 класс
Цилиндр. 4 класс Сфера и шар
Сфера и шар Четыре замечательные точки треугольника. 8 класс
Четыре замечательные точки треугольника. 8 класс Решение задач
Решение задач История появления дробей
История появления дробей  Шар. Радиус. Центр
Шар. Радиус. Центр Метод комплексных амплитуд при моделировании радиосистем. Лекция 12
Метод комплексных амплитуд при моделировании радиосистем. Лекция 12 Сочетательное и распределительное свойство умножения. Урок 1
Сочетательное и распределительное свойство умножения. Урок 1 Уравнение прямой на плоскости
Уравнение прямой на плоскости Комплексные числа
Комплексные числа Відео. Задача на 2 дії
Відео. Задача на 2 дії Задачи на смеси и сплавы
Задачи на смеси и сплавы Корреляционное моделирование
Корреляционное моделирование LP
LP Презентация на тему Статистика
Презентация на тему Статистика  Треугольник. Элементы треугольника
Треугольник. Элементы треугольника Практикум 2
Практикум 2 Презентация на тему ГИА 2013. Модуль ГЕОМЕТРИЯ (№13)
Презентация на тему ГИА 2013. Модуль ГЕОМЕТРИЯ (№13)