Содержание
- 2. Основные разделы: 4.1 Основные определения и понятия 4.2 Способы задания графа 4.3 Операции над графами и
- 3. Теория графов как математическая дисциплина сформировалась в середине 30-х гг. ХХ ст. Термин «граф» впервые появился
- 4. Анализ и синтез цепей и систем; проектирование каналов связи и исследование процессов передачи информации; построение контактных
- 5. сетевое планирование и управление; тактические и логические задачи, головоломки, занимательные игры; выбор оптимальных маршрутов и потоков
- 6. теория множеств, теория матриц, теория групп, математическая логика, численный анализ, теория вероятностей, топология, комбинаторный анализ Связь
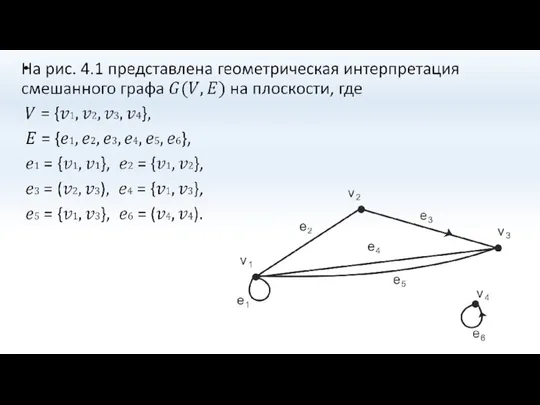
- 7. 4.1 Основные определения и понятия
- 8. Основные определения и понятия
- 9. Граф, состоящий из вершин и соединяющих их ребер, называется неориентированным, а граф, состоящий из вершин и
- 11. Определения
- 12. Смежность и инцидентность
- 13. Некоторая последовательность смежных дуг называется путем, а последовательность смежных ребер называется цепью. Замкнутый путь называется контуром,
- 14. Путь, цепь, контур Цепь (цикл) называется гамильтоновой, если она проходит через все вершины графа по одному
- 15. Связность
- 16. Степень вершины графа
- 17. Число ребер графа
- 18. Следствия
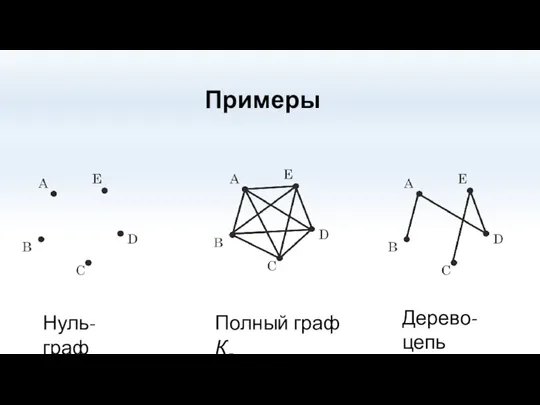
- 19. Нуль-граф Полный граф К5 Примеры Дерево-цепь
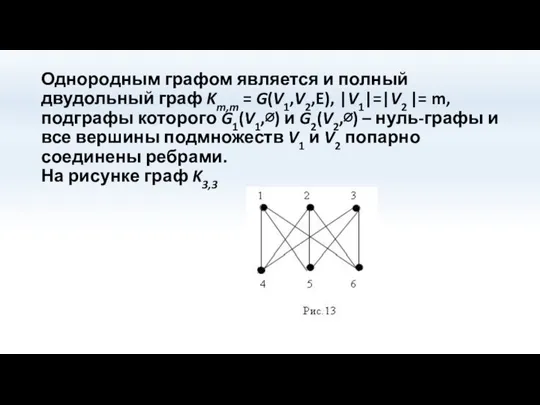
- 20. Однородным графом является и полный двудольный граф Km,m = G(V1,V2,E), |V1|=|V2 |= m, подграфы которого G1(V1,∅)
- 21. Определение двудольного графа Km,n = G(V1,V2,E), Двудольный граф Km,n = G(V1,V2,E), - это граф G(V,E), такой
- 22. Эйлеровы и гамильтоновы цепи и циклы
- 23. Эйлеров цикл Теорема1. Чтобы неориентированный граф обладал эйлеровым циклом, необходимо и достаточно, чтобы он был связан,
- 24. Эйлерова церь
- 25. Алгоритм построения эйлерова цикла
- 26. Гамильтонов цикл
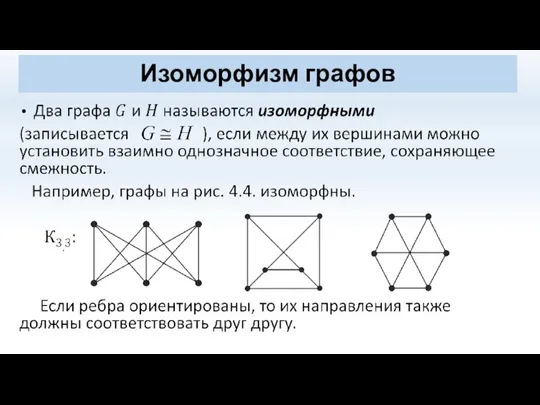
- 27. Изоморфизм графов
- 28. Свойства изоморфных графов
- 29. Планарность. Плоские графы Граф называется планарным, если его можно уложить на плоскости без пересечения ребер. Плоский
- 30. Гомеоморфизм графов
- 31. Теорема Понтрягина-Куратовского Теорема 3. Граф планарен тогда и только тогда, когда он не содержит подграфа, гомеоморфного
- 32. Числа, характеризующие граф
- 33. Хроматическое число графа
- 34. Задача о раскраске географической карты
- 35. 4.2. Способы задания графа Графически; На языке теории множеств; Матричным способом; Списками.
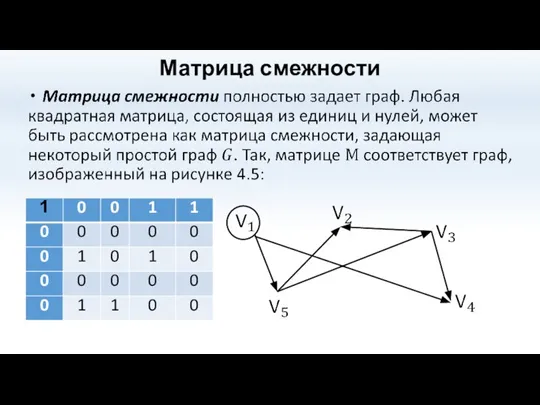
- 36. Матрица смежности
- 37. Для орграфа:
- 38. Для неорграфа:
- 39. Матрица смежности
- 40. Матрица инцидентности
- 42. Матрица инцидентности
- 43. Матрица инцидентности
- 44. Матрица инцидентности
- 45. v1: v2, v3, v4 v2: v4 v3: v4: v1, v3 Задание списком смежностей
- 46. e1: v1, v2 e2: v1, v3 e3: v1, v4 e4: v4, v1 e5: v2, v4 e6:
- 47. 4.3 Операции на графах и их свойства 1. Удаление ребра; 2. Удаление вершины; 3. Добавление вершины;
- 48. 1-4 Операции добавления и удаления
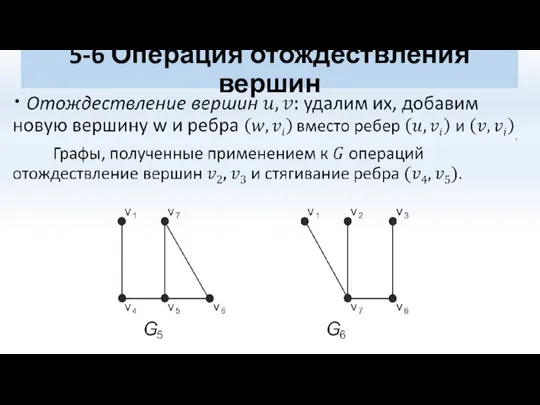
- 49. 5-6 Операция отождествления вершин
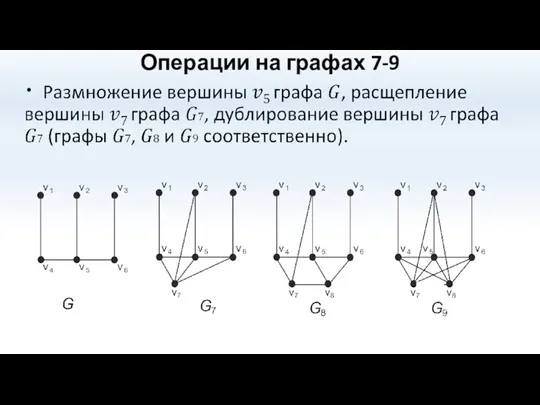
- 50. Операции на графах 7-9
- 51. Операции на графах 7-9
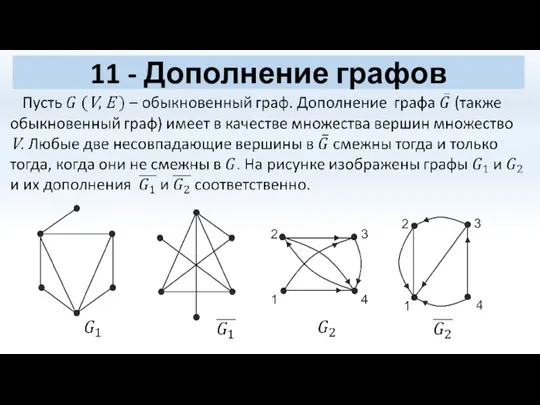
- 52. 11 - Дополнение графов
- 53. Дополнение графов
- 54. Пример 1. Матрицы смежности вершин А графа G2 и графа , изображенных на рис., имеют вид:
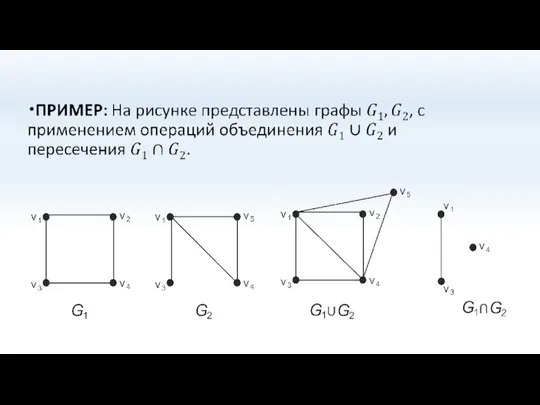
- 55. Объединение графов-12
- 56. Объединение графов
- 57. Объединение графов
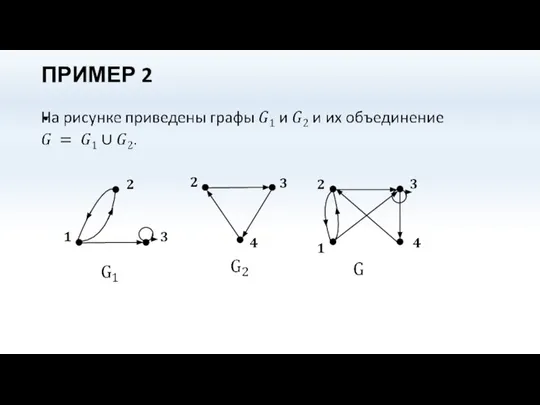
- 58. ПРИМЕР 2
- 59. ПРИМЕР 2 (продолжение) Матрицы смежности вершин графов:
- 60. ПРИМЕР 2 (продолжение) матрицы смежности вершин вспомогательных графов G1′ и G2′ и графа G:
- 61. 13- Пересечение графов
- 62. Пересечение графов
- 63. Пересечение графов
- 64. ПРИМЕР 3
- 65. ПРИМЕР 3 (продолжение) Матрицы смежности вершин исходных графов:
- 66. ПРИМЕР 3 (продолжение) V = V1∩V2 = {1, 2, 3}. Матрицы смежности вершин вспомогательных графов G1′
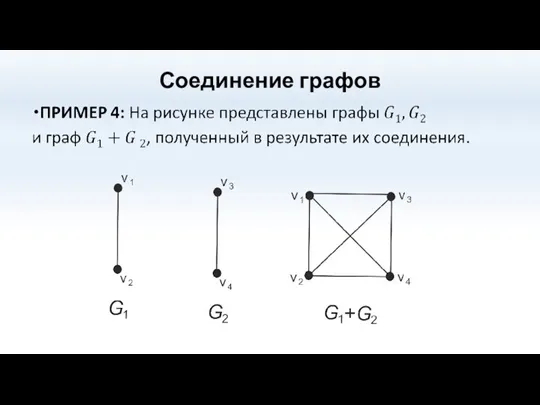
- 68. 14- Соединение графов
- 69. Соединение графов
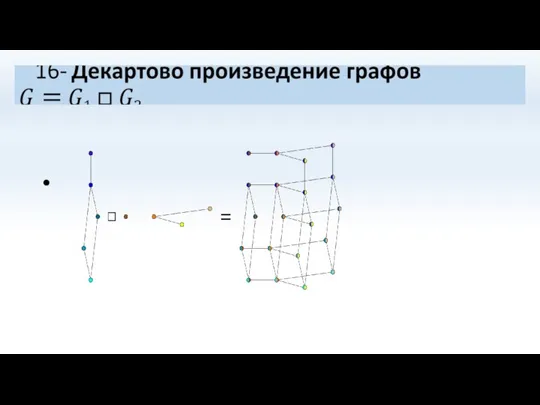
- 70. 15- Композиция графов
- 71. Композиция графов
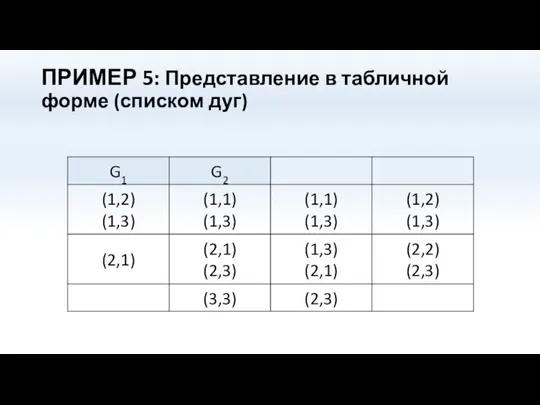
- 73. ПРИМЕР 5: Представление в табличной форме (списком дуг)
- 74. Пример 5 Матрицы смежности вершин исходных графов
- 75. Пример 5
- 79. 4.4 Деревья
- 80. Ориентированные деревья Ориентированные деревья
- 86. Несвязный граф, компонентами связности которого являются деревья, называется лесом.
- 88. Доказательство
- 89. Задача о нефтепроводе (минимальном остовном дереве)
- 90. Задача о нефтепроводе: построение графа
- 91. Задача о нефтепроводе: графическая задача
- 92. Алгоритм Краскала (жадный)
- 93. Алгоритм Прима (алгоритм ближайшего соседа) Идея алгоритма. На каждом шаге алгоритма будем достраивать остовное дерево T(Vt,
- 95. Скачать презентацию















































































 Симметрия в природе
Симметрия в природе Решение задач. Урок 22
Решение задач. Урок 22 Презентация на тему ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ
Презентация на тему ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ  Тест. Округление чисел до десятков, сотен
Тест. Округление чисел до десятков, сотен Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Умножение и деление дробей
Умножение и деление дробей Математика в лицах
Математика в лицах Решение задач на проценты. Концентрация
Решение задач на проценты. Концентрация Проценты. Проценты в древности
Проценты. Проценты в древности Многоэтажные дроби. 8 класс
Многоэтажные дроби. 8 класс Подготовка к контрольной работе
Подготовка к контрольной работе Естественно балансирующееся общество
Естественно балансирующееся общество Способы решения задач на смеси и сплавы
Способы решения задач на смеси и сплавы Дидактические материалы на уроках математики
Дидактические материалы на уроках математики Действия с величинами. Урок №4
Действия с величинами. Урок №4 Аксиомы стереометрии
Аксиомы стереометрии Практикум по решению задач
Практикум по решению задач Числовые функции
Числовые функции Сокращение дробей
Сокращение дробей Устное решение задач по готовым чертежам
Устное решение задач по готовым чертежам Аксиомы стереометрии
Аксиомы стереометрии Математическая викторина
Математическая викторина Решение показательных уравнений. 10 класс. Учебник С. М. Никольского
Решение показательных уравнений. 10 класс. Учебник С. М. Никольского Математическая статистика. Формула классической вероятности
Математическая статистика. Формула классической вероятности Площадь многоугольника
Площадь многоугольника Исследование функций и построение графиков
Исследование функций и построение графиков Основы теории вероятностей или случайные события ( лекция 2)
Основы теории вероятностей или случайные события ( лекция 2) Дисперсионный анализ
Дисперсионный анализ