Слайд 2Вычисли:
Найти область значений функции:

Слайд 9Свойства функции
1. ООФ- множество всех чисел.
2. Нечётная функция.
3. Возрастает на Убывает на
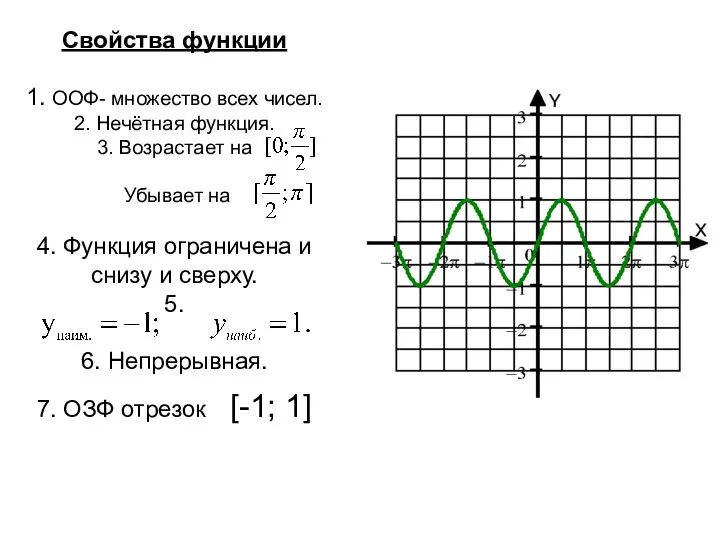
4. Функция ограничена и снизу и сверху.
5.
6. Непрерывная.
7. ОЗФ отрезок [-1; 1]
Слайд 10Р.Декарт (1596-1650г.г.)
Ф.Виет (1540-1603)
Л.Эйлер (1707-1783)
Пифагор (около 580г. до н.э.- 500г. до н.э.

Слайд 11Тригонометрические функции возникли в Древней Греции в связи с исследованиями в астрономии

и геометрии. Понятия синуса и косинуса встречаются уже в 3 веке до н.э. в работах Евклида, Архимеда и др.
Современную форму тригонометрии придал Л. Эйлер. Ему принадлежат определения тригонометрических функций и принятая в наши дни символика.
Слайд 12ООФ: у=sinx
2. ОЗФ: у=sinx+1
3. График функции у=sinx+1
4. График функции у=sin(x+ )
5.
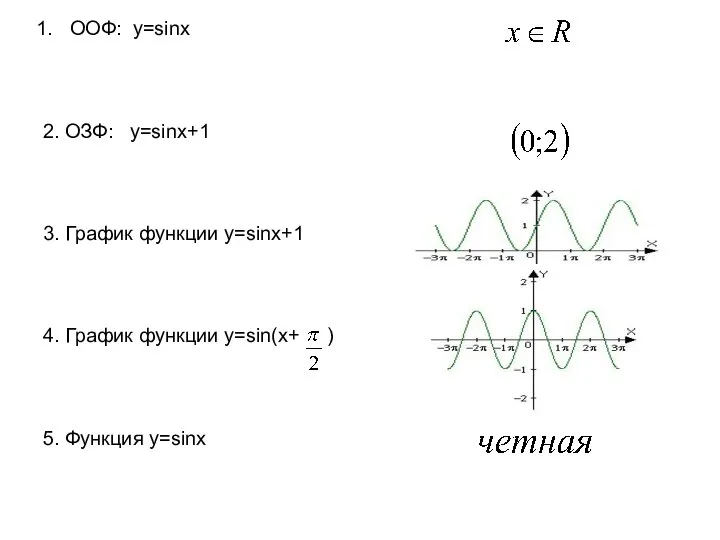
Функция y=sinx





 Взаимное расположение двух прямых в пространстве
Взаимное расположение двух прямых в пространстве Практикум. Демографические задачи
Практикум. Демографические задачи Тренажёры ЕГЭ
Тренажёры ЕГЭ Не ошибись! 56 = 78= 34= 60+4 80+6 90+3 30+60 10+40 50+20 77-7 48-8 26-6 50-40 60-20 80-10
Не ошибись! 56 = 78= 34= 60+4 80+6 90+3 30+60 10+40 50+20 77-7 48-8 26-6 50-40 60-20 80-10 Что такое медиана?
Что такое медиана? Закрепление таблицы умножения и деления
Закрепление таблицы умножения и деления Трикутники. Елементи трикутника
Трикутники. Елементи трикутника Симметрия вокруг нас
Симметрия вокруг нас Средняя линия треугольника
Средняя линия треугольника Способы задания зависимостей между величинами: аналитический, табличный, графический
Способы задания зависимостей между величинами: аналитический, табличный, графический Арифметические действия с десятичными дробями. Математический тренажёр
Арифметические действия с десятичными дробями. Математический тренажёр Понятие цилиндра
Понятие цилиндра Интерактивная игра Состав числа в пределах первого десятка
Интерактивная игра Состав числа в пределах первого десятка Возмущения линейных систем и проматрицы
Возмущения линейных систем и проматрицы Инженерно-вычислительные технологии
Инженерно-вычислительные технологии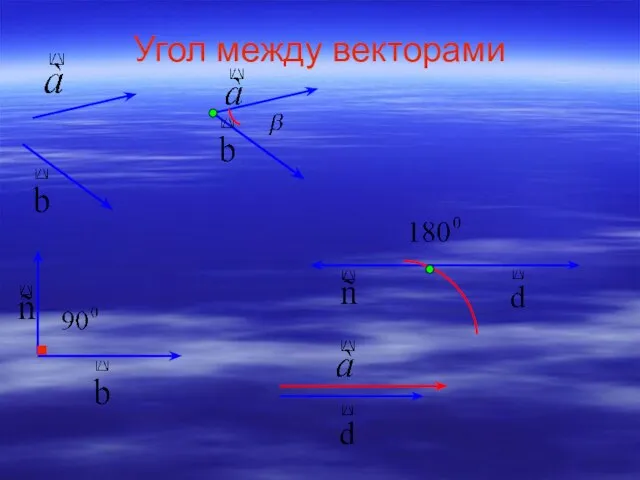 Презентация на тему Угол между векторами и скалярное произведение векторов
Презентация на тему Угол между векторами и скалярное произведение векторов  Построение симметричных фигур
Построение симметричных фигур Объемы тел вращения
Объемы тел вращения Методы решения тригонометрических уравнений. 10 класс
Методы решения тригонометрических уравнений. 10 класс Аксиомы стереометрии. Взаимное расположение прямых и плоскостей в пространстве
Аксиомы стереометрии. Взаимное расположение прямых и плоскостей в пространстве Графический метод решения уравнений с параметром
Графический метод решения уравнений с параметром Развертка сферы
Развертка сферы Математический диктант. Классная работа
Математический диктант. Классная работа Презентация на тему Начертательная геометрия
Презентация на тему Начертательная геометрия  Презентация на тему Итоговое повторение курса алгебры за 8 класс
Презентация на тему Итоговое повторение курса алгебры за 8 класс  тригонометрия 1 урок
тригонометрия 1 урок Принятие решений о прикреплении оптовых потребителей к поставщикам
Принятие решений о прикреплении оптовых потребителей к поставщикам К В Н 8 – 9 классы «И прекрасна, и сильна Математика – страна»
К В Н 8 – 9 классы «И прекрасна, и сильна Математика – страна»