Факультативное занятие. Лабиринт. 6 класс

Слово «лабиринт» греческого происхождения, означает подземный ход.

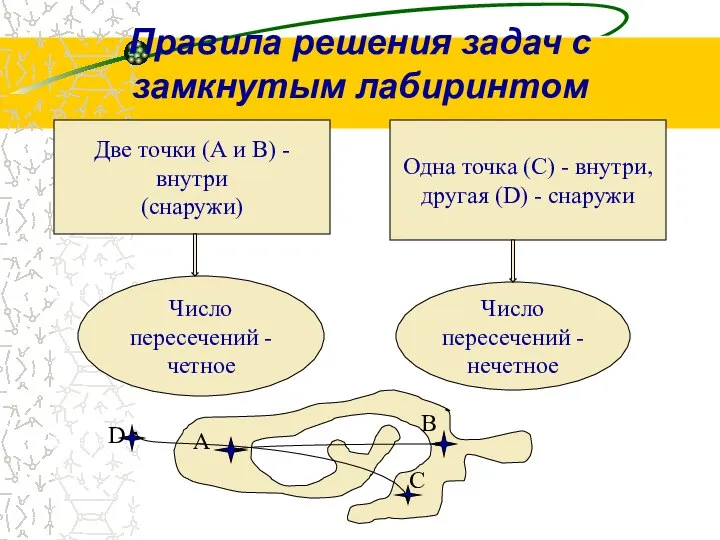
Правила решения задач с замкнутым лабиринтом
Две точки (А и В) -
внутри
(снаружи)
Одна точка (С) - внутри,
другая (D) - снаружи
Число
пересечений -
четное
Число
пересечений -
нечетное
А
В
D
С

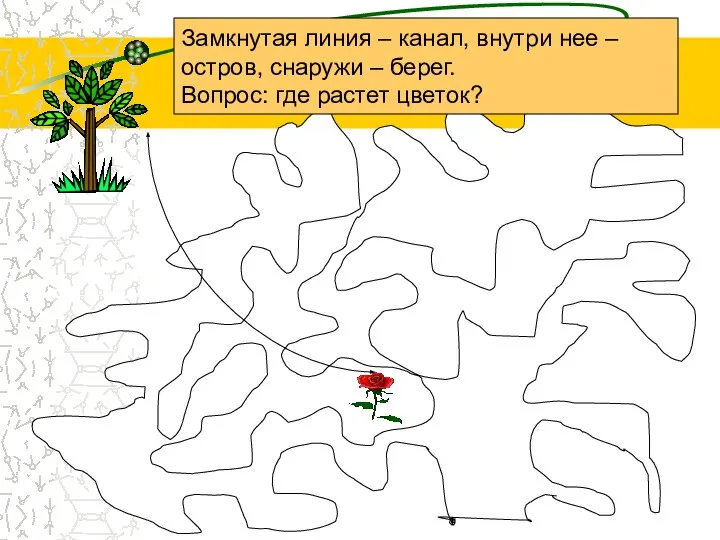
Замкнутая линия – канал, внутри нее –
остров, снаружи – берег.
Вопрос: где растет цветок?

ИСПОЛЬЗОВАНИЕ ЛАБИРИНТОВ
РАЗВЛЕЧЕНИЯ
Франция ХII в.
лабиринты выкладывали мозаикой на полу собора
Англия -
живые изгороди
НАКАЗАНИЯ

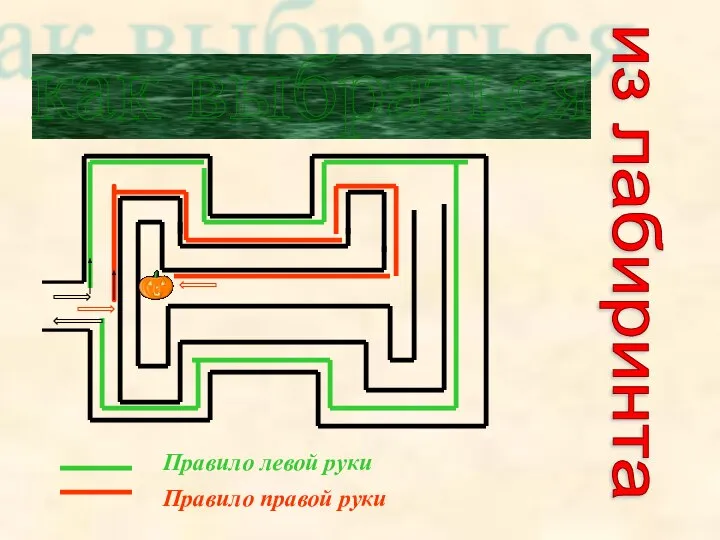
Правило левой руки
Правило правой руки
как выбраться
из лабиринта

всегда ли есть
выход ?

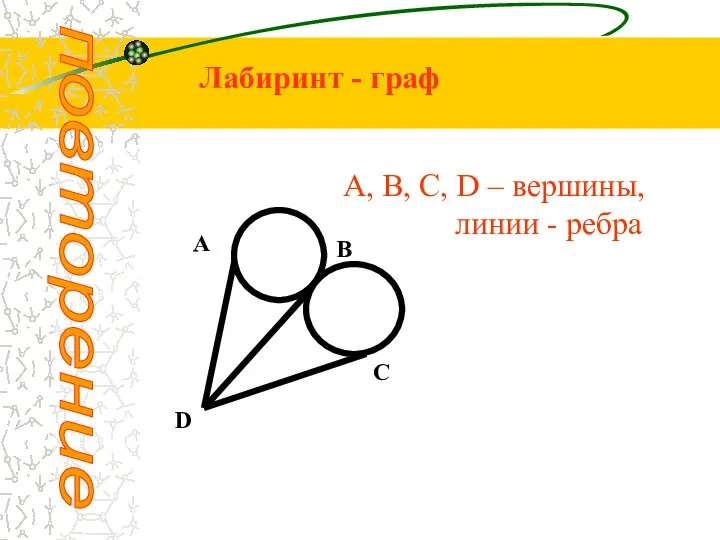
повторение
Лабиринт - граф
А
В
С
D
A, В, С, D – вершины,
линии - ребра

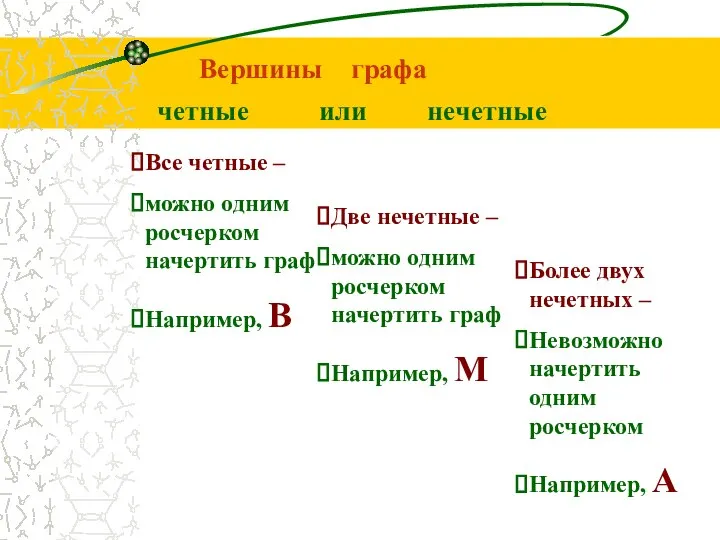
Вершины графа
Все четные –
можно одним росчерком начертить граф
Например, В
Две нечетные –
можно одним росчерком начертить граф
Например, М
Более двух нечетных –
Невозможно начертить одним росчерком
Например, А
четные или нечетные

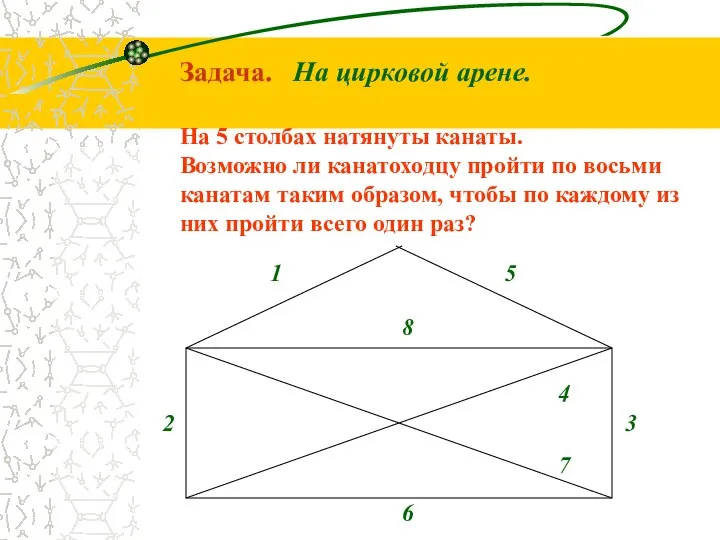
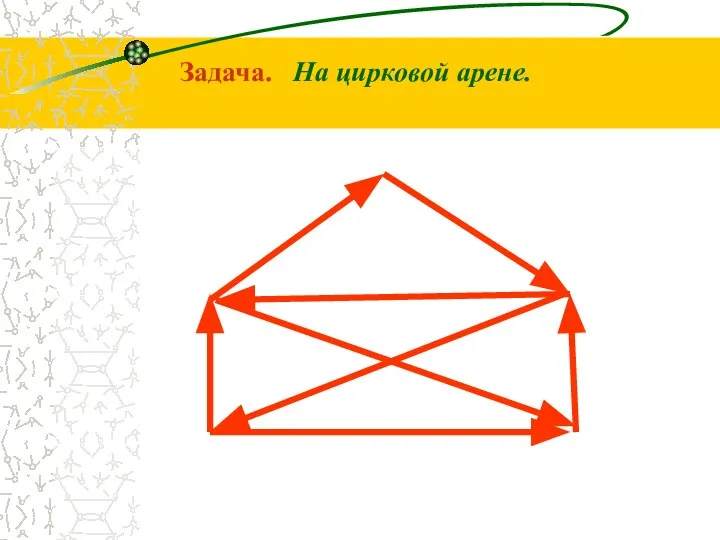
Задача. На цирковой арене.
На 5 столбах натянуты канаты.
Возможно ли канатоходцу пройти по восьми канатам таким образом, чтобы по каждому из них пройти всего один раз?
1
2
3
4
5
6
7
8

Задача. На цирковой арене.

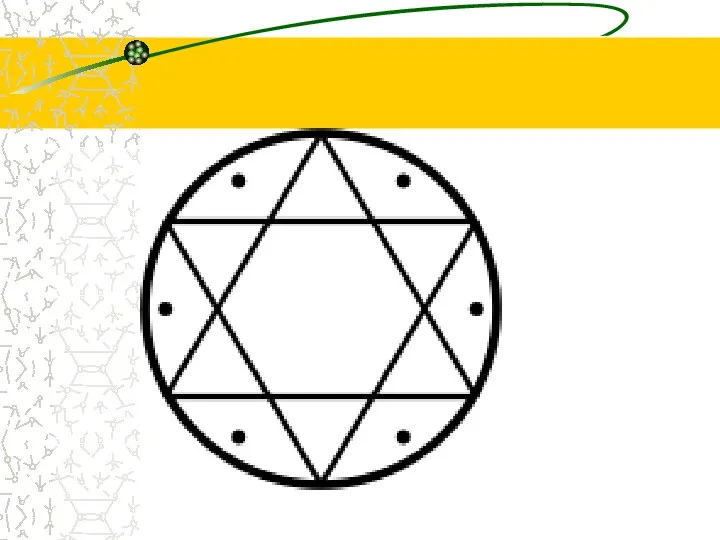
всегда ли есть
выход ?

Если мы обойдем весь лабиринт, побывав в каждом коридоре на пути туда и на пути обратно, то все ребра графа удвоятся.
Тогда каждая вершина заведомо будет четной и, следовательно, такой граф можно обойти за один обход.
Таким образом, безвыходных лабиринтов нет.

У Р А !
ВЫХОД ЕСТЬ
В С Е Г Д А