Содержание
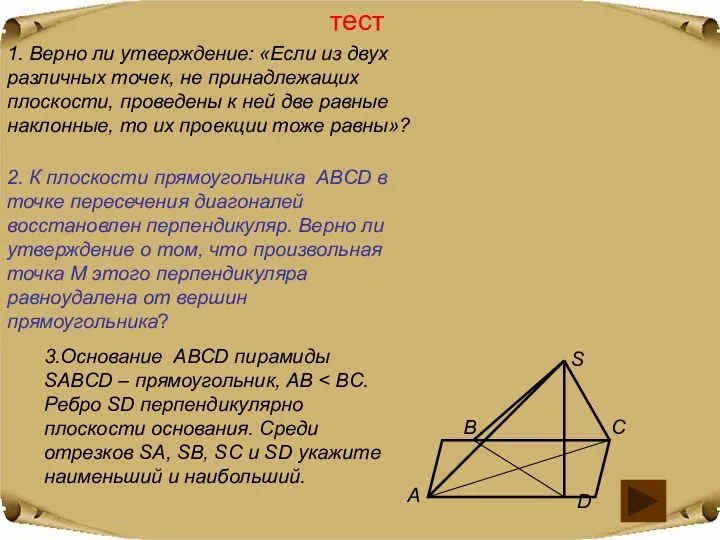
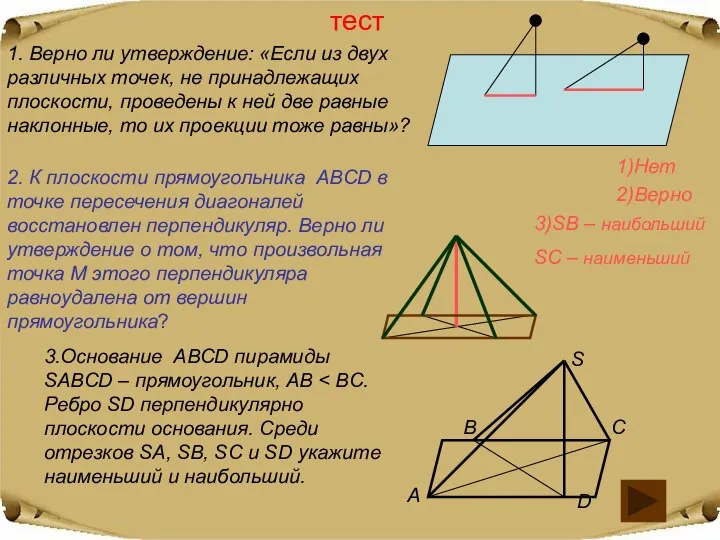
- 2. тест 1. Верно ли утверждение: «Если из двух различных точек, не принадлежащих плоскости, проведены к ней
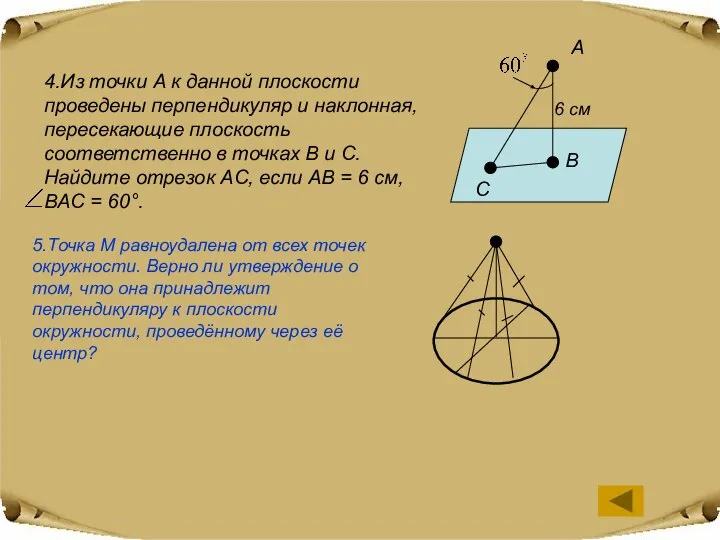
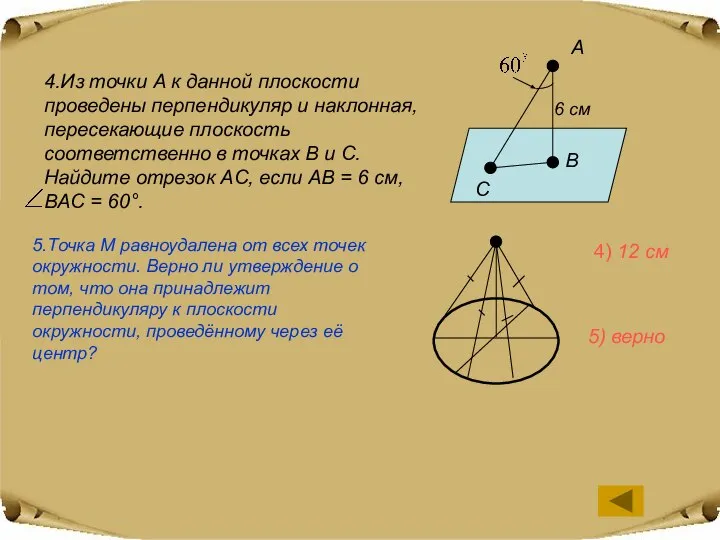
- 3. 4.Из точки A к данной плоскости проведены перпендикуляр и наклонная, пересекающие плоскость соответственно в точках B
- 4. тест 1. Верно ли утверждение: «Если из двух различных точек, не принадлежащих плоскости, проведены к ней
- 5. 4.Из точки A к данной плоскости проведены перпендикуляр и наклонная, пересекающие плоскость соответственно в точках B
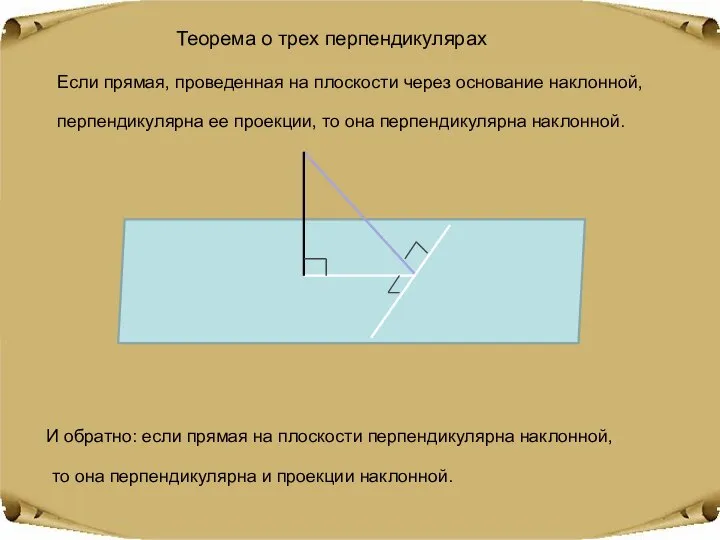
- 6. Теорема о трех перпендикулярах Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то
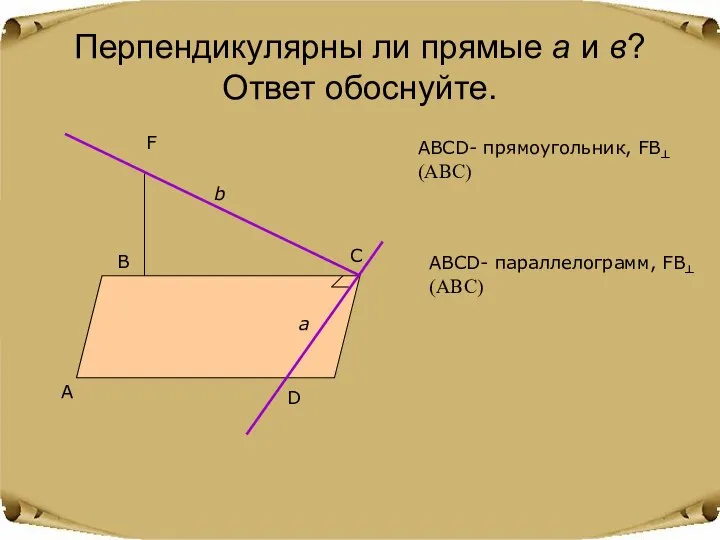
- 7. Перпендикулярны ли прямые а и в? Ответ обоснуйте. А В С D F b a ABCD-
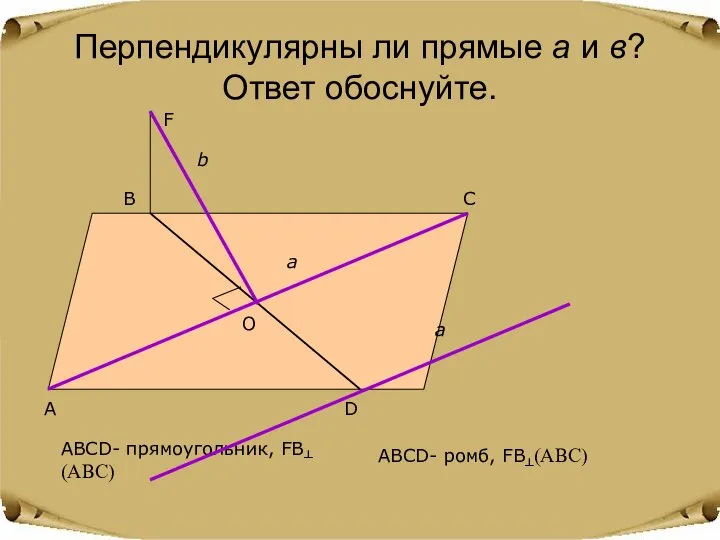
- 8. Перпендикулярны ли прямые а и в? Ответ обоснуйте. А D C B O F b a
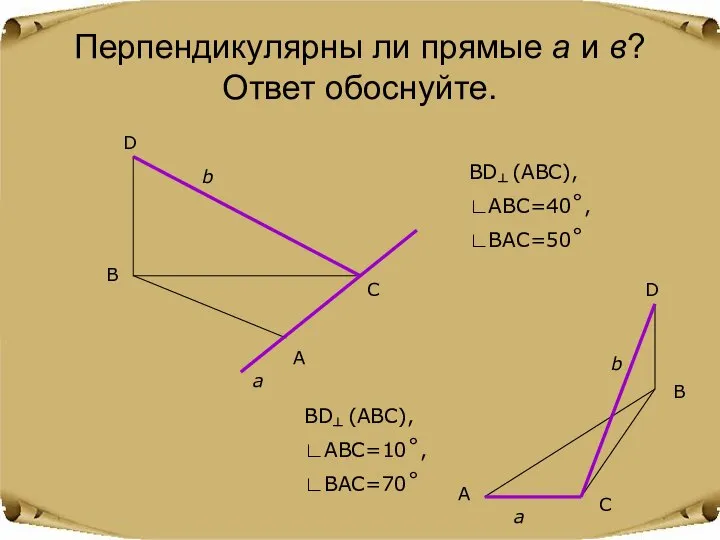
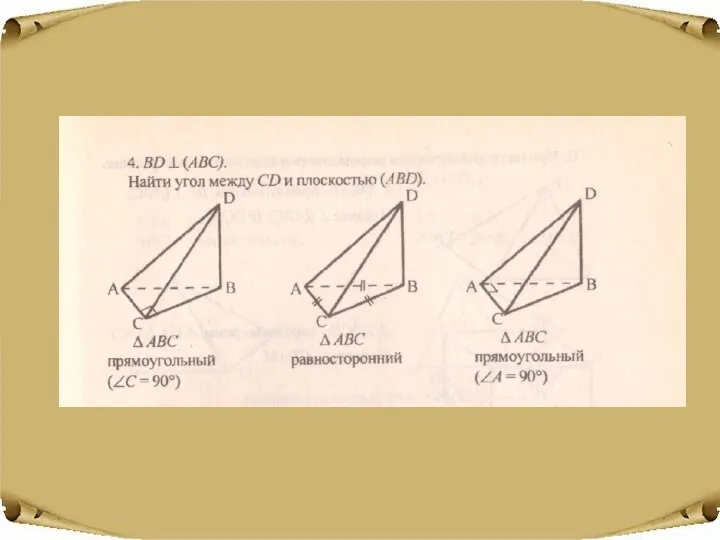
- 9. Перпендикулярны ли прямые а и в? Ответ обоснуйте. B A C D a b BD┴ (ABC),
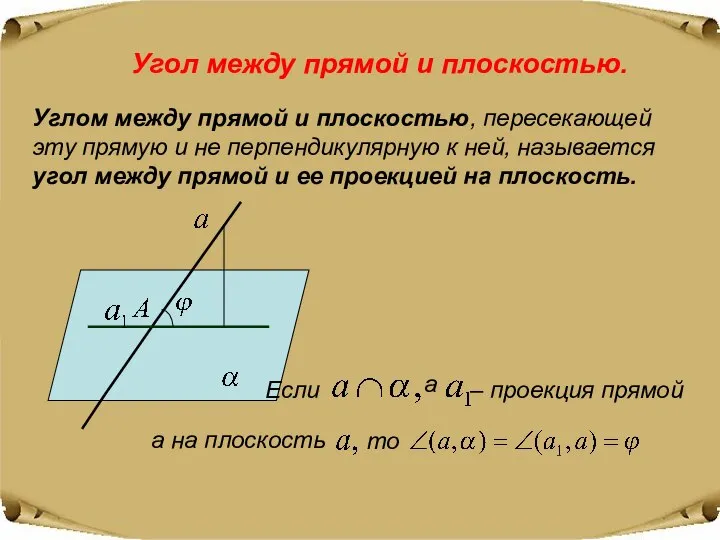
- 10. Угол между прямой и плоскостью. Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярную
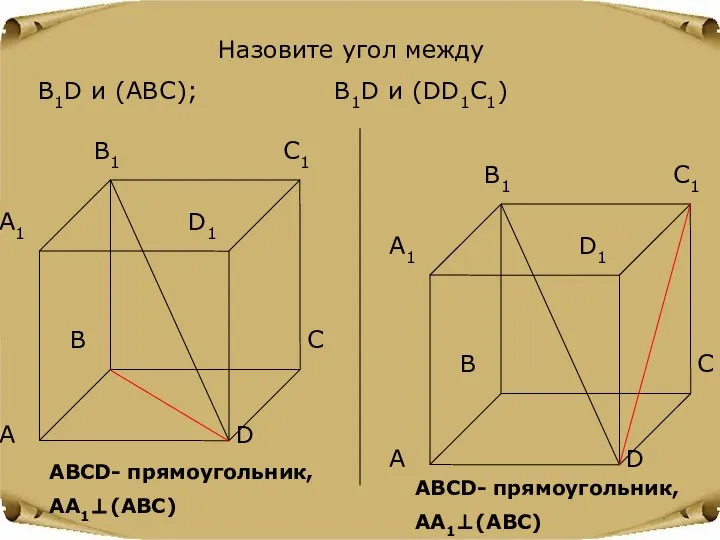
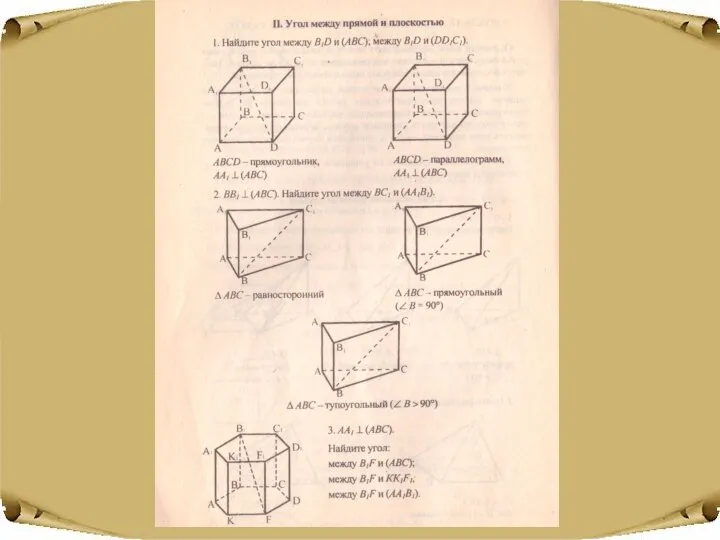
- 11. Назовите угол между В1D и (ABC); В1D и (DD1C1) АВСD- прямоугольник, АА1⊥(АВС) АВСD- прямоугольник, АА1⊥(АВС)
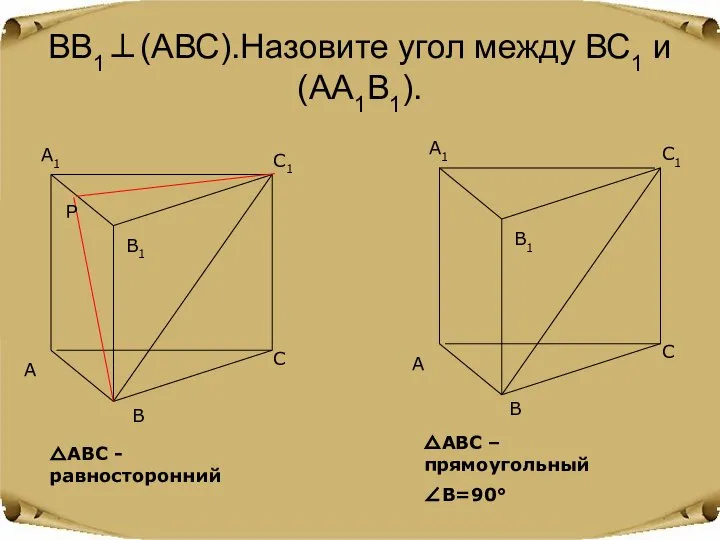
- 12. ВВ1⊥(АВС).Назовите угол между ВС1 и (АА1В1). △АВС - равносторонний △АВС – прямоугольный ∠В=90° Р
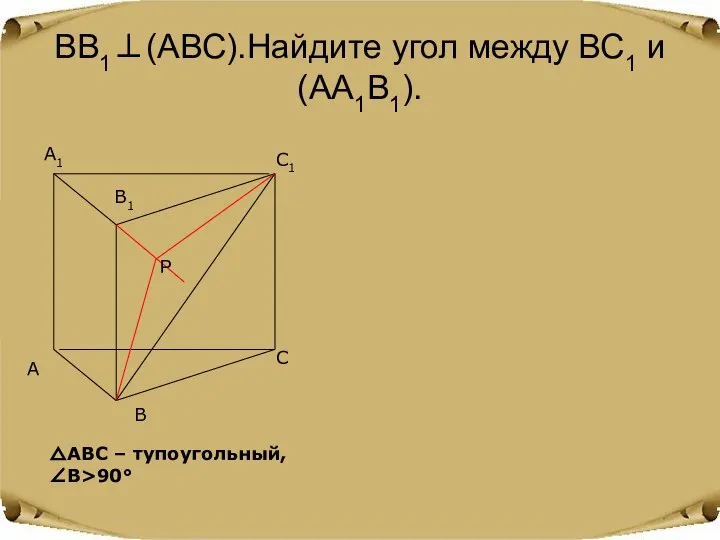
- 13. ВВ1⊥(АВС).Найдите угол между ВС1 и (АА1В1). △АВС – тупоугольный, ∠В>90° Р
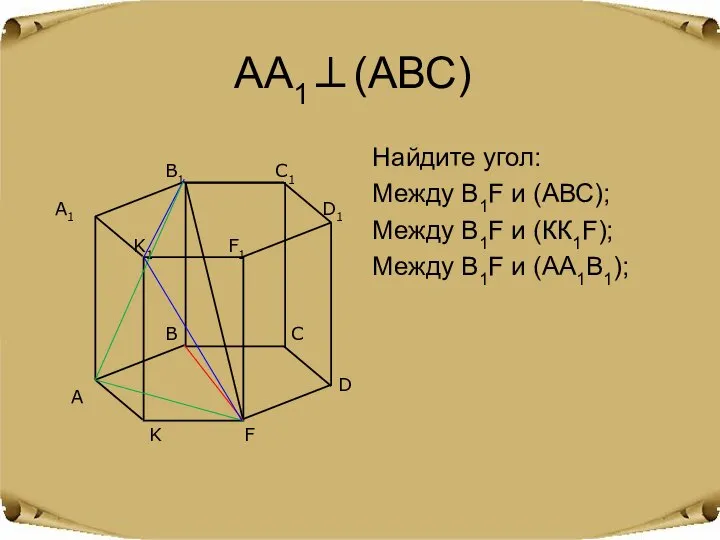
- 14. АА1⊥(АВС) Найдите угол: Между В1F и (АВС); Между В1F и (КК1F); Между В1F и (АА1В1);
- 15. Схема построения линейного угла между плоскостями Выделить линию пересечения плоскостей и определить, есть ли плоскость ей
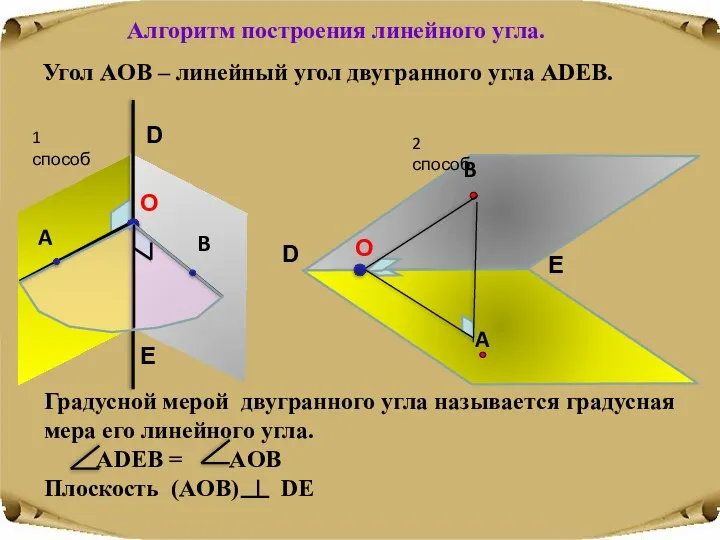
- 16. Угол AОB – линейный угол двугранного угла ADEB. D E Градусной мерой двугранного угла называется градусная
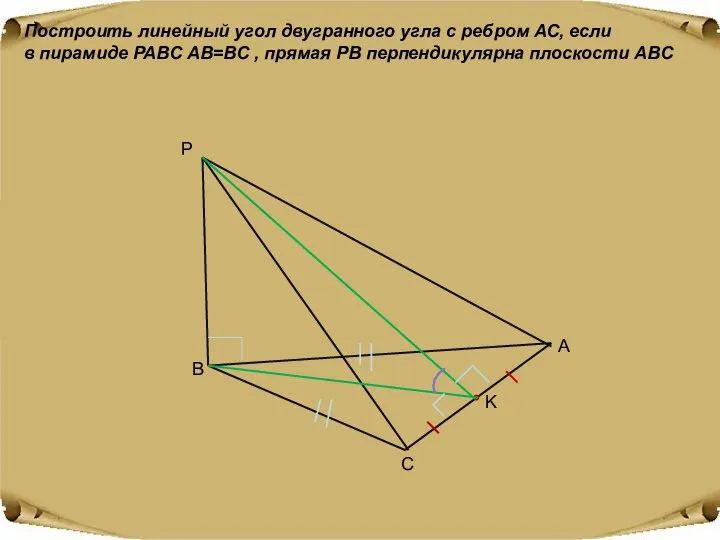
- 17. Построить линейный угол двугранного угла с ребром АС, если в пирамиде PABC AB=BC , прямая PB
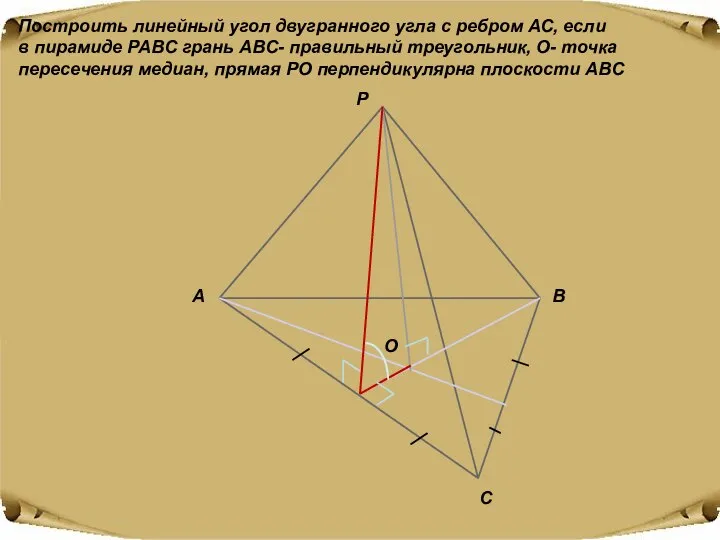
- 18. Построить линейный угол двугранного угла с ребром АС, если в пирамиде PABC грань ABC- правильный треугольник,
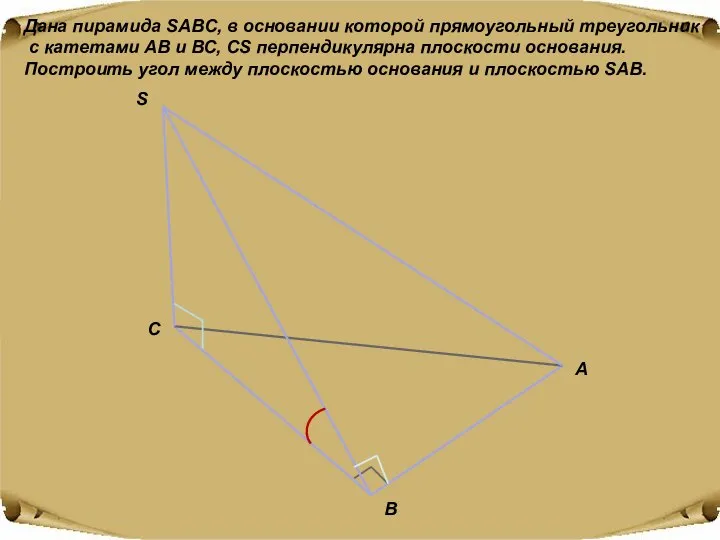
- 19. Дана пирамида SAВC, в основании которой прямоугольный треугольник с катетами АВ и ВС, СS перпендикулярна плоскости
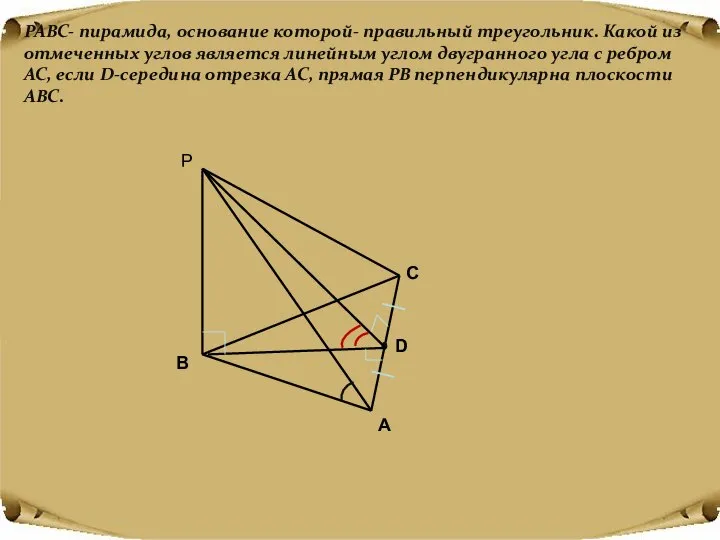
- 20. PABC- пирамида, основание которой- правильный треугольник. Какой из отмеченных углов является линейным углом двугранного угла с
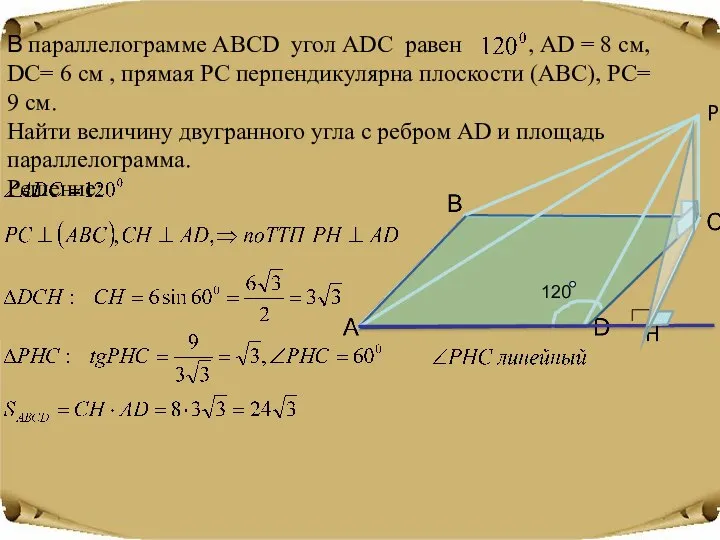
- 21. В параллелограмме АВСD угол АDС равен , АD = 8 см, DС= 6 см , прямая
- 25. Скачать презентацию

 Электронное пособие. Основные понятия и определения в математике
Электронное пособие. Основные понятия и определения в математике Рекурсивные алгоритмы
Рекурсивные алгоритмы Графики элементарных функций. Повторение
Графики элементарных функций. Повторение Движение. Его виды и применение. 9 класс
Движение. Его виды и применение. 9 класс Презентация на тему Использование графов в решении логических задач
Презентация на тему Использование графов в решении логических задач  Применение функциональных зависимостей в реальных процессах и явлениях
Применение функциональных зависимостей в реальных процессах и явлениях Графики. График движения
Графики. График движения Теорема о свойстве биссектрисы с доказательством
Теорема о свойстве биссектрисы с доказательством Иррациональные уравнения (часть 1)
Иррациональные уравнения (часть 1) Арктангенс и арккотангенс
Арктангенс и арккотангенс Множественные связи. Порядковые и категоризованные переменные
Множественные связи. Порядковые и категоризованные переменные Падпрасторы лінейнай прасторы
Падпрасторы лінейнай прасторы Решение задач
Решение задач Выражение (для печатной и электронной формы учебника)
Выражение (для печатной и электронной формы учебника) Геометрический диктант
Геометрический диктант Практическое применение площадей геометрических фигур
Практическое применение площадей геометрических фигур Неравенства (9 класс)
Неравенства (9 класс) Площадь фигуры. Сравнение площадей
Площадь фигуры. Сравнение площадей Спиннеры и метематика
Спиннеры и метематика Аксиомы стереометрии
Аксиомы стереометрии Математическая викторина В гостях у мудрой совы 2 класс
Математическая викторина В гостях у мудрой совы 2 класс Повторение изученного материала. 1 класс
Повторение изученного материала. 1 класс Организации проектной деятельности
Организации проектной деятельности Решение тригонометрических неравенств
Решение тригонометрических неравенств Презентация на тему Решение систем неравенств (8 класс)
Презентация на тему Решение систем неравенств (8 класс)  Решение задач по теме Параллельные прямые
Решение задач по теме Параллельные прямые Решение задач на применение признаков подобия
Решение задач на применение признаков подобия Признаки равенства треугольников. Задачи на готовых чертежах
Признаки равенства треугольников. Задачи на готовых чертежах