Решение уравнения методом последовательных приближений

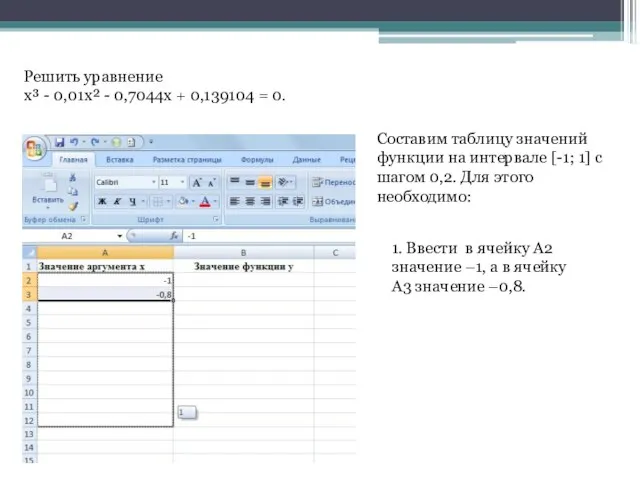
1. Ввести в ячейку A2 значение –1, а в ячейку A3 значение –0,8.
Решить уравнение
x³ - 0,01x² - 0,7044x + 0,139104 = 0.
Составим таблицу значений функции на интервале [-1; 1] с шагом 0,2. Для этого необходимо:

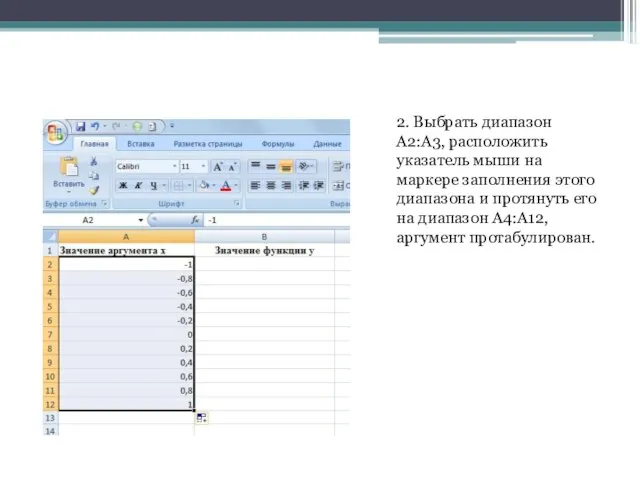
2. Выбрать диапазон A2:A3, расположить указатель мыши на маркере заполнения этого диапазона и протянуть его на диапазон A4:A12, аргумент протабулирован.

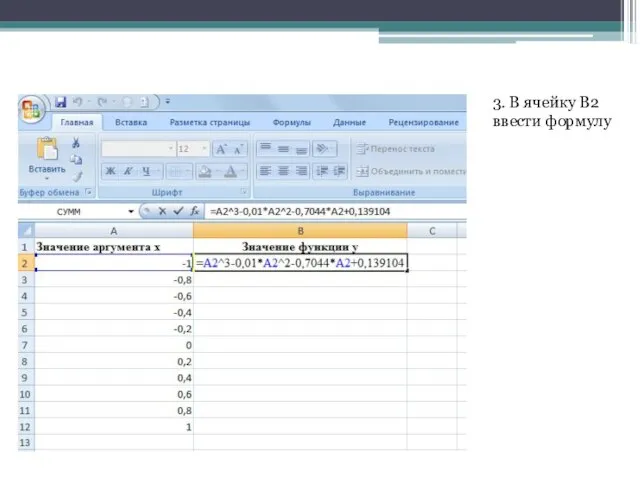
3. В ячейку B2 ввести формулу

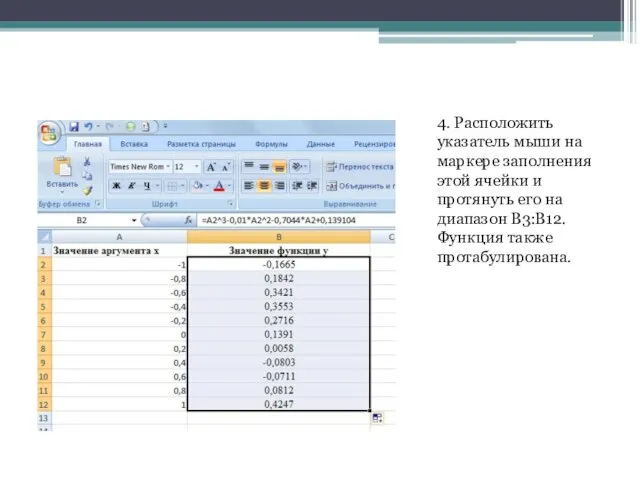
4. Расположить указатель мыши на маркере заполнения этой ячейки и протянуть его на диапазон B3:B12. Функция также протабулирована.

Из таблицы видно, что полином меняет знак на интервалах [-1; -0,8], [0,2; 0,4] и [0,6; 0,8], и поэтому на каждом из этих интервалов имеется свой корень. Так как полином третьей степени имеет не более трех корней, то они все локализованы.

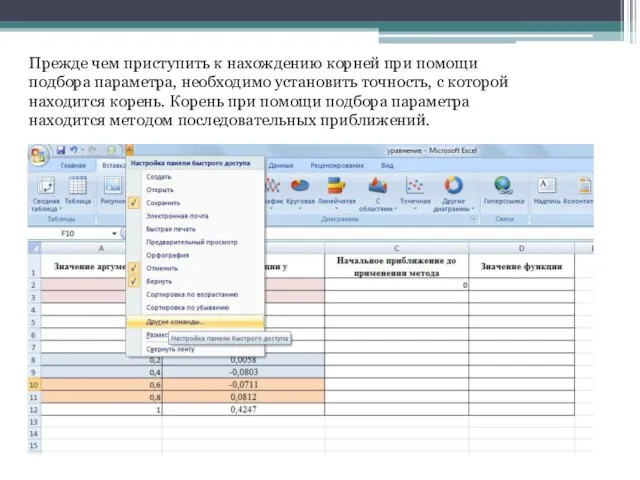
Прежде чем приступить к нахождению корней при помощи подбора параметра, необходимо установить точность, с которой находится корень. Корень при помощи подбора параметра находится методом последовательных приближений.

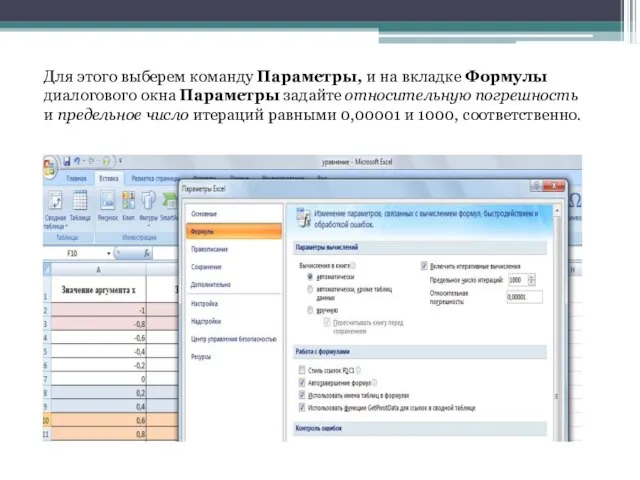
Для этого выберем команду Параметры, и на вкладке Формулы диалогового окна Параметры задайте относительную погрешность и предельное число итераций равными 0,00001 и 1000, соответственно.

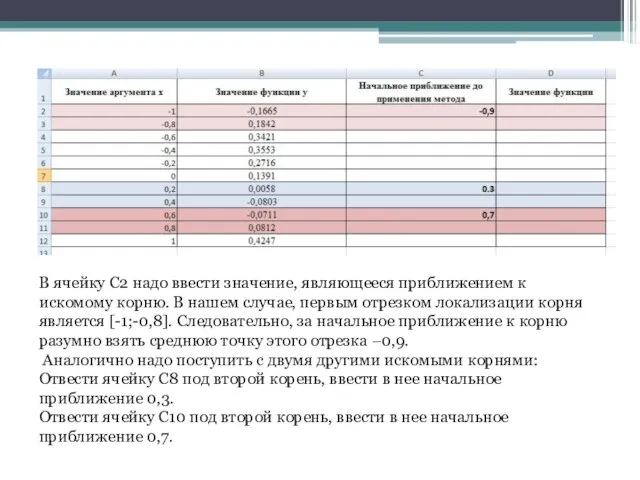
В ячейку C2 надо ввести значение, являющееся приближением к искомому корню. В нашем случае, первым отрезком локализации корня является [-1;-0,8]. Следовательно, за начальное приближение к корню разумно взять среднюю точку этого отрезка –0,9.
Аналогично надо поступить с двумя другими искомыми корнями:
Отвести ячейку C8 под второй корень, ввести в нее начальное приближение 0,3.
Отвести ячейку C10 под второй корень, ввести в нее начальное приближение 0,7.

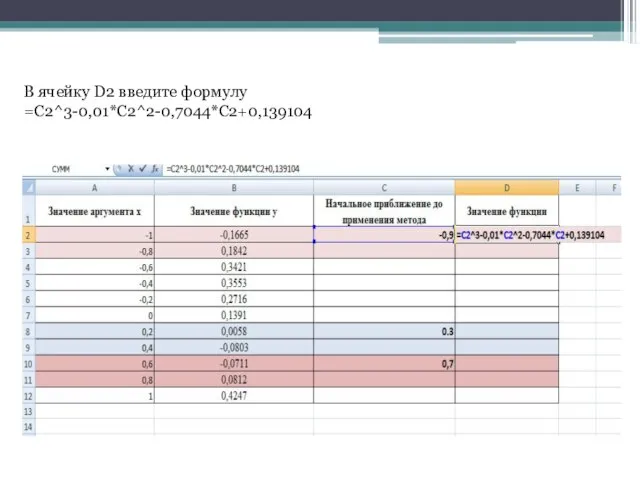
В ячейку D2 введите формулу
=C2^3-0,01*C2^2-0,7044*C2+0,139104

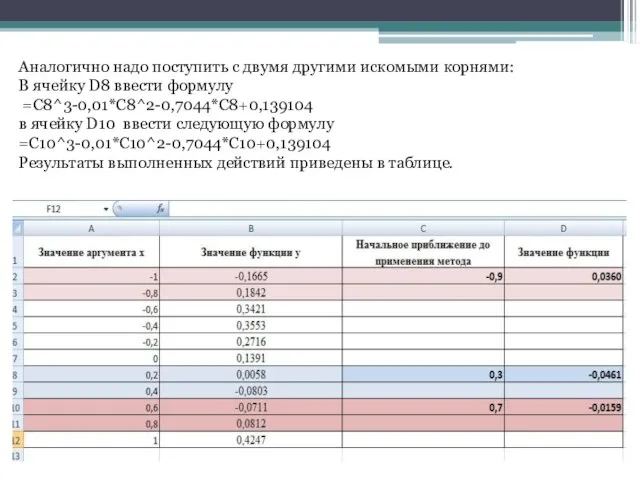
Аналогично надо поступить с двумя другими искомыми корнями:
В ячейку D8 ввести формулу =C8^3-0,01*C8^2-0,7044*C8+0,139104
в ячейку D10 ввести следующую формулу
=C10^3-0,01*C10^2-0,7044*C10+0,139104
Результаты выполненных действий приведены в таблице.

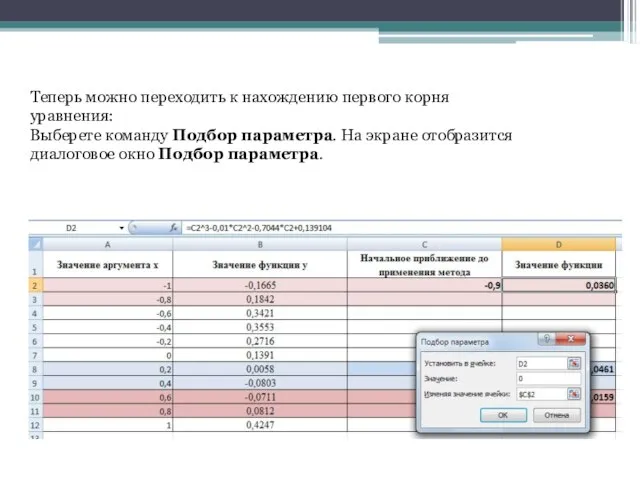
Теперь можно переходить к нахождению первого корня уравнения:
Выберете команду Подбор параметра. На экране отобразится диалоговое окно Подбор параметра.

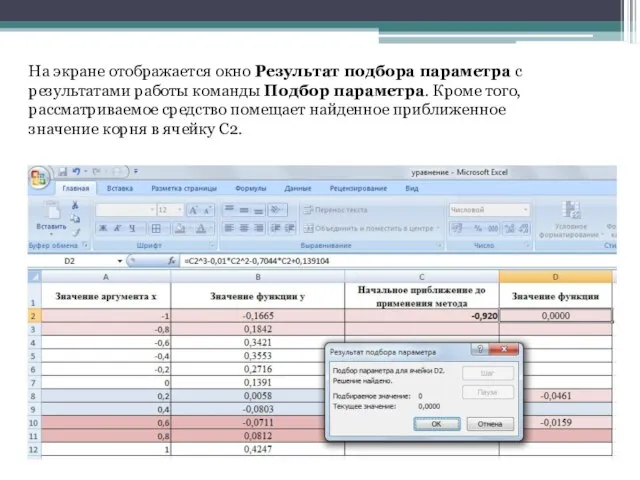
На экране отображается окно Результат подбора параметра с результатами работы команды Подбор параметра. Кроме того, рассматриваемое средство помещает найденное приближенное значение корня в ячейку C2.