Слайд 2На рисунке график
y =f(x) и касательная
к нему в точке
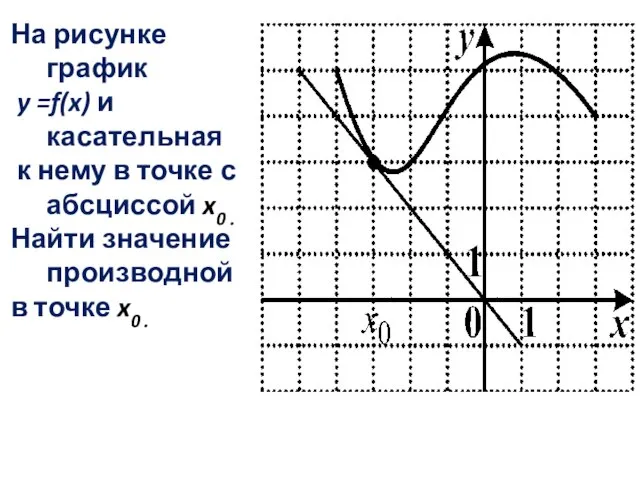
с абсциссой x0 .
Найти значение производной
в точке x0 .
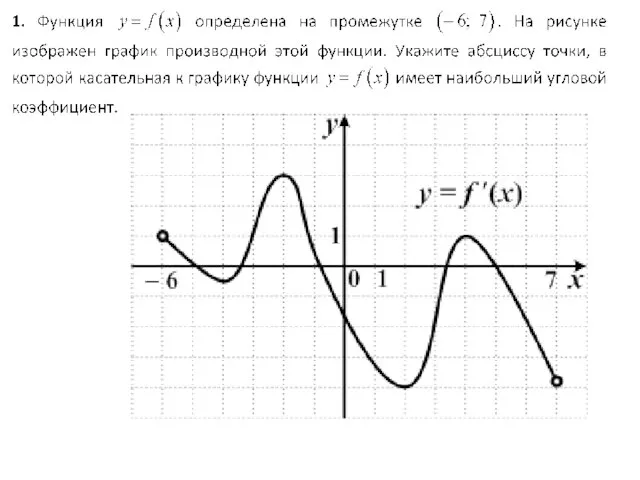
Слайд 3 На рисунке изображен график
функции и касательная к нему
в точке с
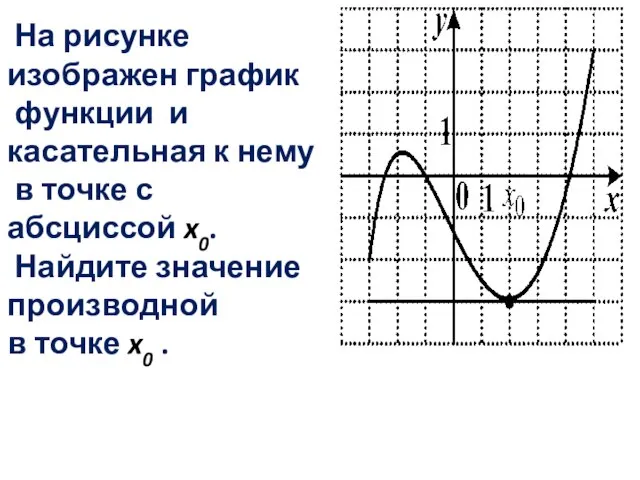
абсциссой x0.
Найдите значение производной
в точке x0 .
Слайд 6Функция определена на промежутке . Используя изображенный на рисунке график производной ,
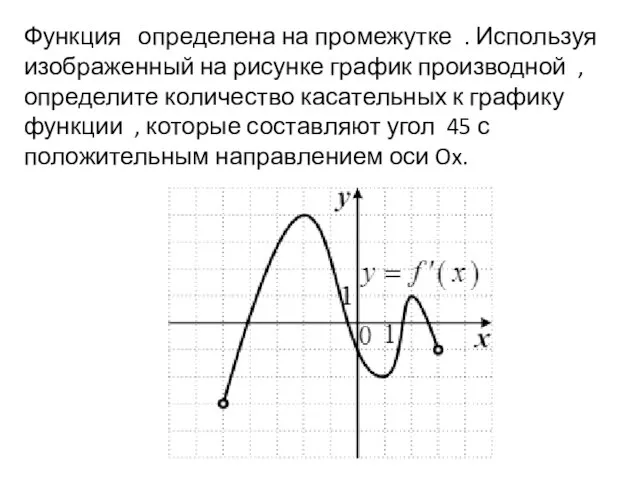
определите количество касательных к графику функции , которые составляют угол 45 с положительным направлением оси Ox.
Слайд 7Функция определена на промежутке . На рисунке изображен график производной . Определите
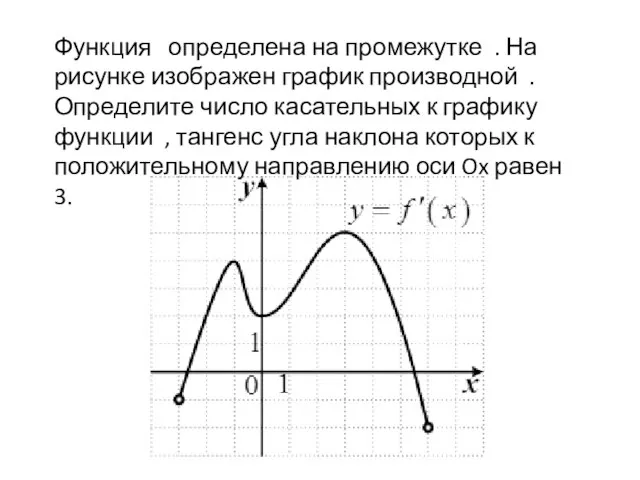
число касательных к графику функции , тангенс угла наклона которых к положительному направлению оси Ox равен 3.
Слайд 8. Функция определена на промежутке . На рисунке изображен график производной этой
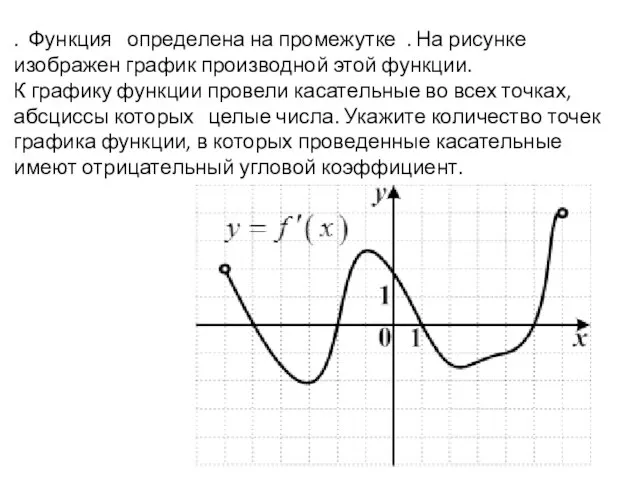
функции.
К графику функции провели касательные во всех точках, абсциссы которых целые числа. Укажите количество точек графика функции, в которых проведенные касательные имеют отрицательный угловой коэффициент.
Слайд 9Функция определена на промежутке . Используя изображенный на рисунке график производной ,
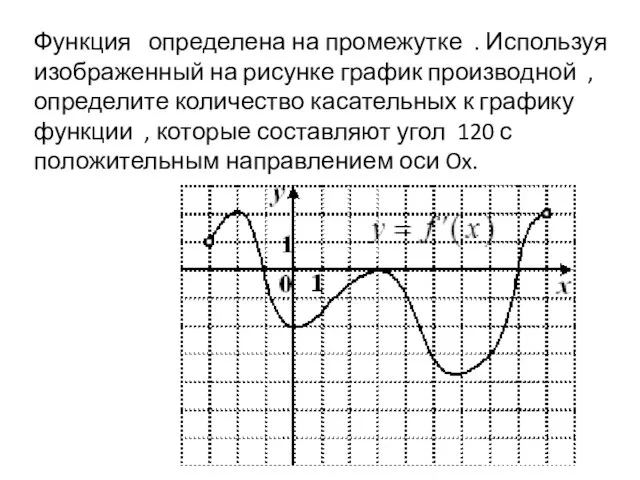
определите количество касательных к графику функции , которые составляют угол 120 с положительным направлением оси Ox.







 Пересечение поверхностей, одна из которых занимает проецирующее положение относительно плоскости проекций
Пересечение поверхностей, одна из которых занимает проецирующее положение относительно плоскости проекций Презентация на тему Деление десятичной дроби на натуральное число
Презентация на тему Деление десятичной дроби на натуральное число  Углы в треугольниках
Углы в треугольниках Презентация на тему Математическая викторина
Презентация на тему Математическая викторина  Задача по математике (1 класс, задание 13.2)
Задача по математике (1 класс, задание 13.2) Работа переменной силы
Работа переменной силы Определение логарифма
Определение логарифма Умножение. Законы умножения
Умножение. Законы умножения Виды треугольников
Виды треугольников Тетраэдр. Противоположные ребра
Тетраэдр. Противоположные ребра Презентация на тему Единицы массы (4 класс)
Презентация на тему Единицы массы (4 класс)  Презентация на тему ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ УРАВНЕНИЙ
Презентация на тему ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ УРАВНЕНИЙ  Соотношение между сторонами и углами треугольника
Соотношение между сторонами и углами треугольника Устный счёт. 1 класс
Устный счёт. 1 класс Памятка по оформлению краткой записи к задачам. 1-2 класс
Памятка по оформлению краткой записи к задачам. 1-2 класс Презентация на тему Игра "О, счастливчик, юный математик"
Презентация на тему Игра "О, счастливчик, юный математик"  Тренажер по логарифмам
Тренажер по логарифмам 1 признак подобия треугольников
1 признак подобия треугольников Вероятность события (часть 1)
Вероятность события (часть 1) Золотое сечение
Золотое сечение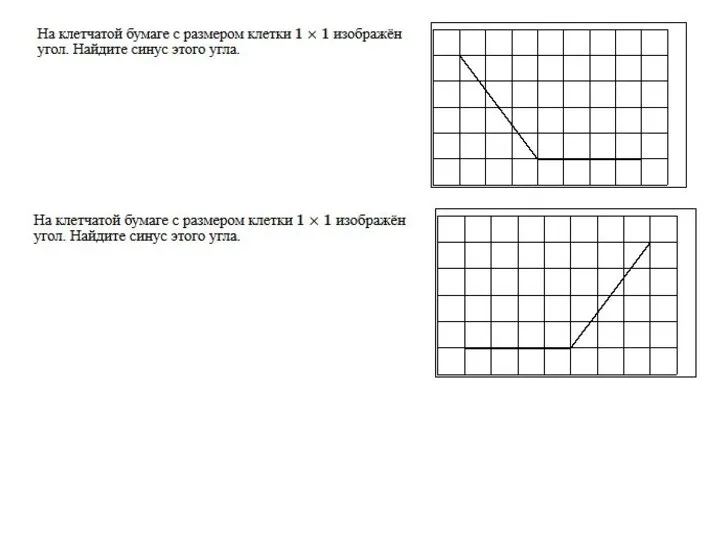 ЕГЭ. Решение задач
ЕГЭ. Решение задач Точка перегиба
Точка перегиба Счет до 10
Счет до 10 Устный счёт Прицепи вагоны. 2 класс
Устный счёт Прицепи вагоны. 2 класс Математика задача. Решение задачи уч. Стр.92 №2
Математика задача. Решение задачи уч. Стр.92 №2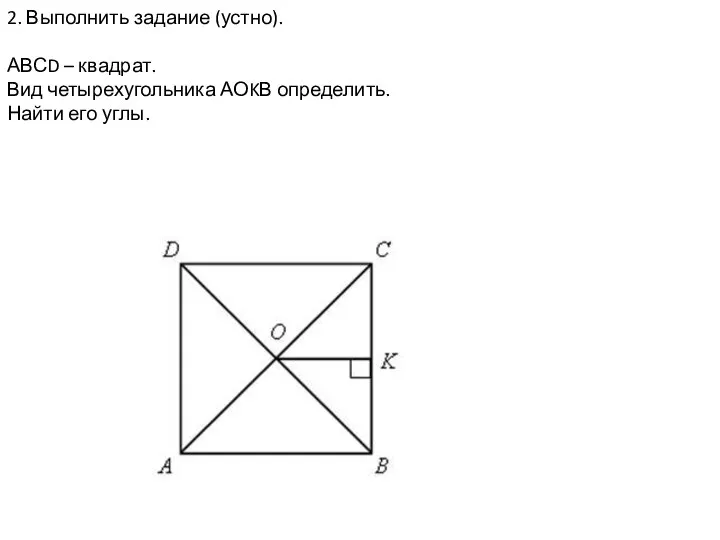 Параллелограмм и трапеция. Урок 7
Параллелограмм и трапеция. Урок 7 Кривые Безье
Кривые Безье Презентация по математике "Праздник чисел «5 плюс »" -
Презентация по математике "Праздник чисел «5 плюс »" -