Призма и ее виды

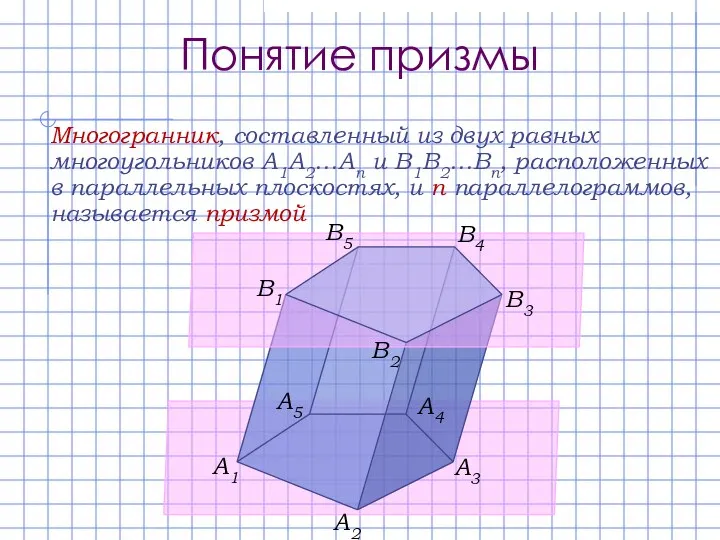
Понятие призмы
Многогранник, составленный из двух равных многоугольников A1A2…An и B1B2…Bn, расположенных в параллельных плоскостях, и n параллелограммов, называется призмой
A1
A2
A3
A4
A5
В1
В2
В3
В4
В5

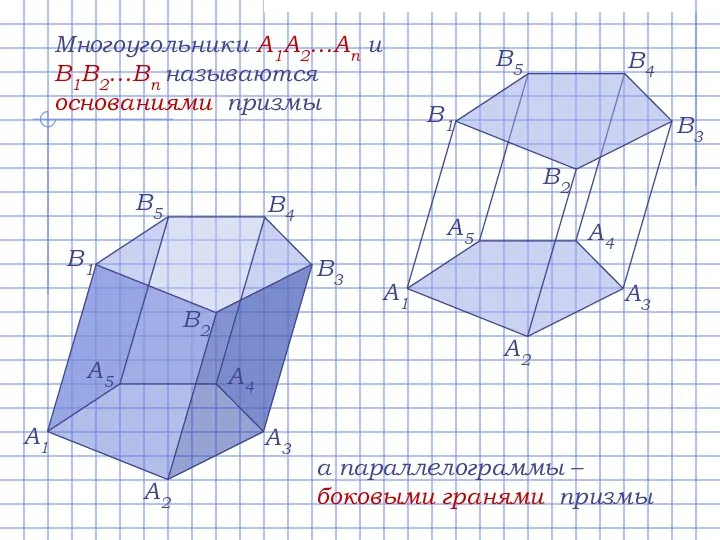
Многоугольники A1A2…An и B1B2…Bn называются основаниями призмы
а параллелограммы – боковыми гранями призмы
A1
A2
A3
A4
A5
В1
В2
В3
В4
В5
A1
A2
A3
A4
A5
В1
В2
В3
В4
В5

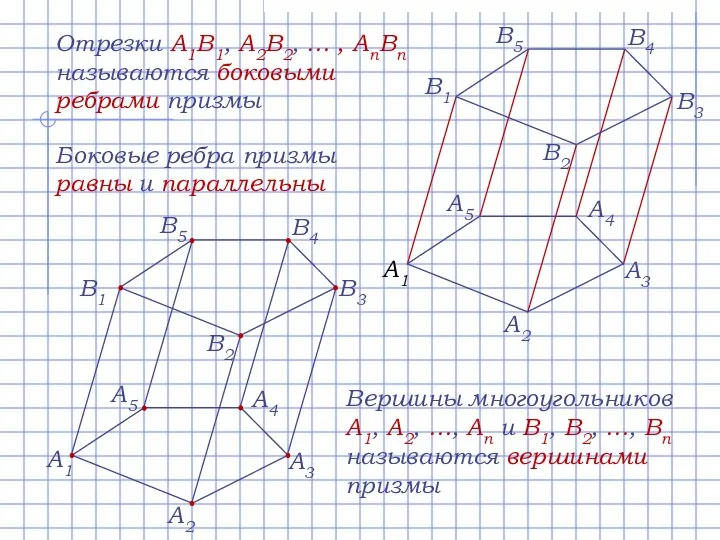
Отрезки A1B1, A2B2, … , AnBn называются боковыми ребрами призмы
Боковые ребра призмы равны и параллельны
A1
A2
A3
A4
A5
В1
В2
В3
В4
В5
A1
A2
A3
A4
A5
В1
В2
В3
В4
В5
Вершины многоугольников A1, A2, …, An и B1, B2, …, Bn называются вершинами призмы

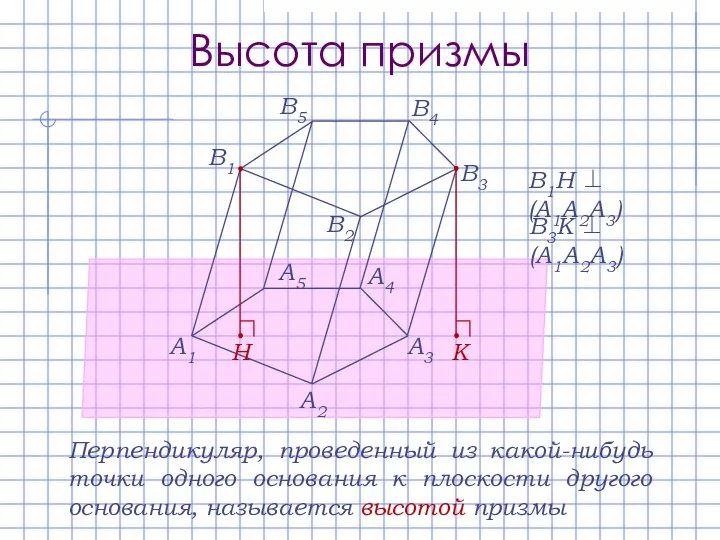
Высота призмы
A1
A2
A3
A4
A5
В1
В2
В3
В4
В5
К
Н
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы
В1Н ⊥(А1А2А3)
В3К ⊥(А1А2А3)

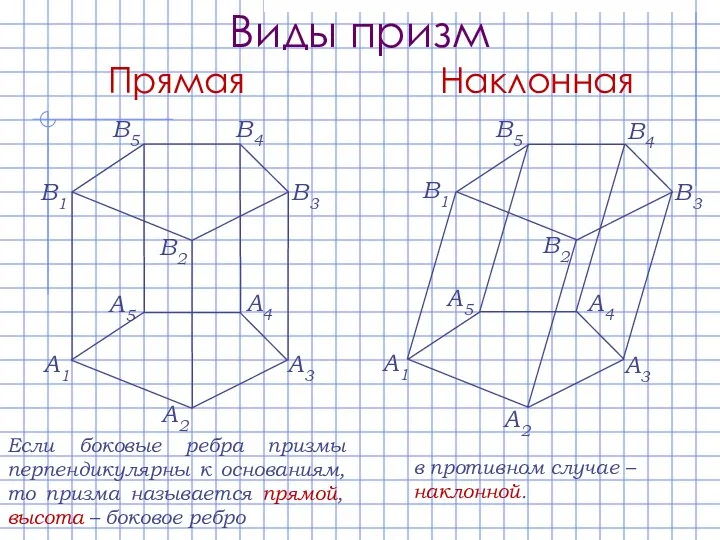
Виды призм
A1
A2
A3
A4
A5
В1
В2
В3
В4
В5
Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой, высота – боковое ребро
A1
A2
A3
A4
A5
В1
В2
В3
В4
В5
в противном случае – наклонной.
Прямая
Наклонная

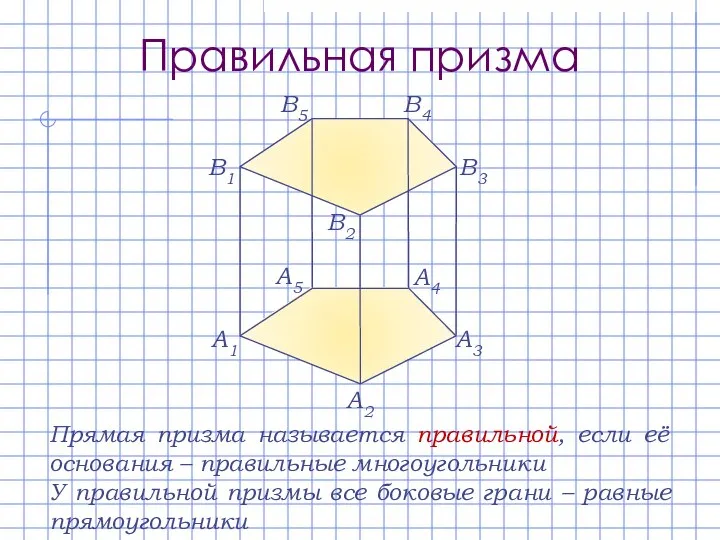
Правильная призма
A1
A2
A3
A4
A5
В1
В2
В3
В4
В5
Прямая призма называется правильной, если её основания – правильные многоугольники
У правильной призмы все боковые грани – равные прямоугольники

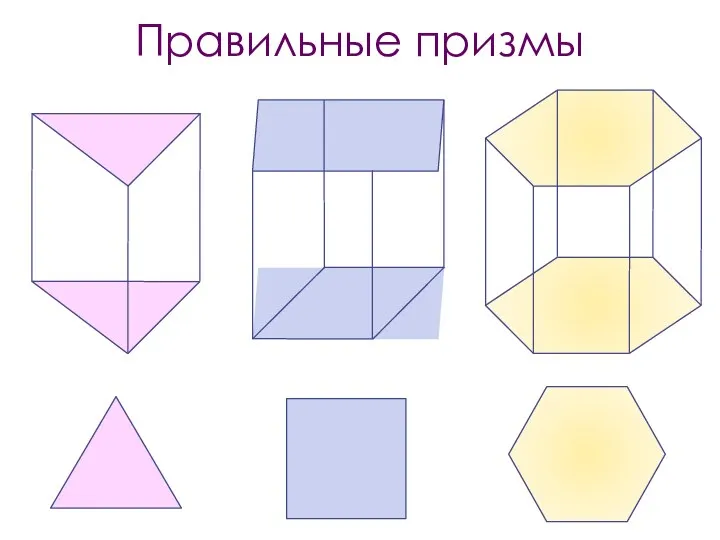
Правильные призмы

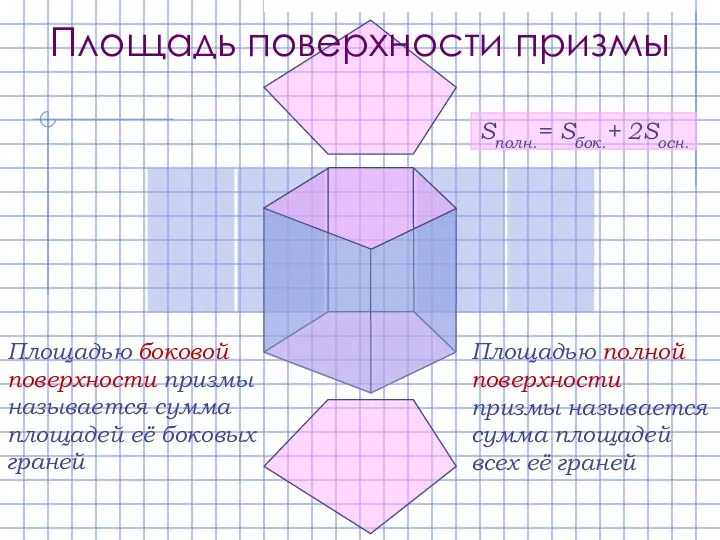
Площадью боковой поверхности призмы называется сумма площадей её боковых граней
Площадью полной поверхности призмы называется сумма площадей всех её граней
Площадь поверхности призмы
Sполн.= Sбок.+ 2Sосн.

Теорема о площади боковой поверхности прямой призмы
Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы
Доказательство.
Боковые грани прямой призмы – прямоугольники, основания которых – стороны основания призмы, а высоты равны высоте h призмы.
Sбок. = A1A2· h + A2A3· h + A3A4· h + … + An-1An· h =
= (A1A2 + A2A3 + A3A4 + … + An-1An) · h = Pосн.· h
Sбок. = Росн.· h

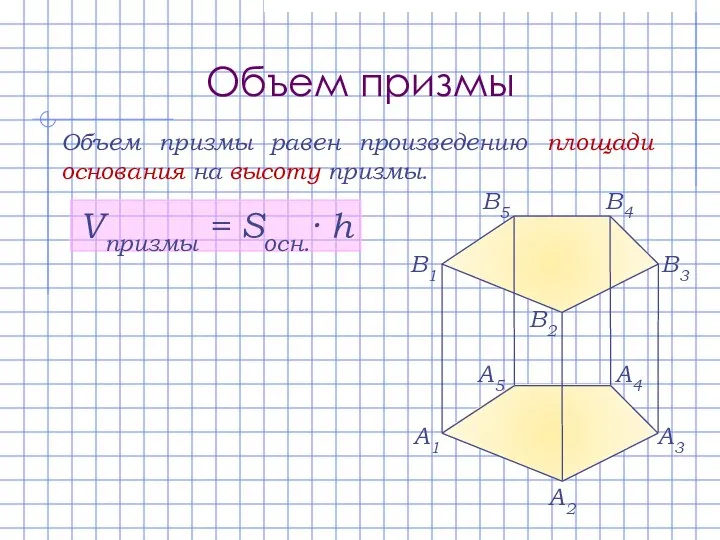
Объем призмы
Объем призмы равен произведению площади основания на высоту призмы.
Vпризмы = Sосн.· h

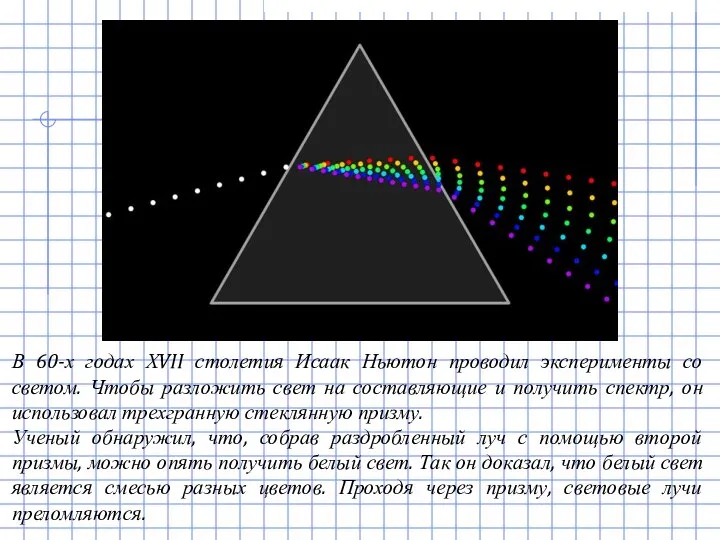
В 60-х годах ХVII столетия Исаак Ньютон проводил эксперименты со светом. Чтобы разложить свет на составляющие и получить спектр, он использовал трехгранную стеклянную призму.
Ученый обнаружил, что, собрав раздробленный луч с помощью второй призмы, можно опять получить белый свет. Так он доказал, что белый свет является смесью разных цветов. Проходя через призму, световые лучи преломляются.

«Я затемнил мою комнату, − писал он, − и сделал очень маленькое отверстие в ставне для пропуска солнечного света».
На пути солнечного луча ученый поставил особое трехгранное стеклышко – призму. На противоположной стене он увидел разноцветную полоску – спектр. Ньютон объяснил это тем, что призма разложила белый цвет на составляющие его цвета. Ньютон первый разгадал, что солнечный луч многоцветный.

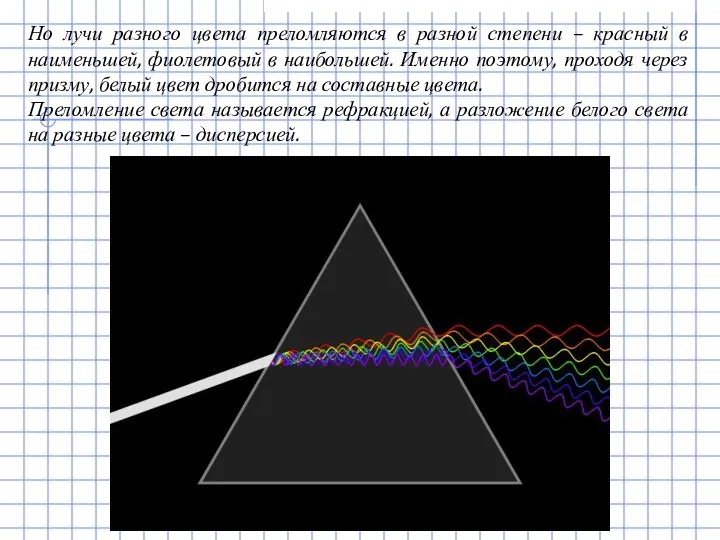
Но лучи разного цвета преломляются в разной степени – красный в наименьшей, фиолетовый в наибольшей. Именно поэтому, проходя через призму, белый цвет дробится на составные цвета.
Преломление света называется рефракцией, а разложение белого света на разные цвета – дисперсией.

Использование призмы для творческих фотоэффектов

Использование призмы для творческих фотоэффектов

Архитектура, оптика, медицина, электронная техника.
(очки, бинокли, объективы, телефоны)

Применение призм в лечении косоглазия
Принцип тренировки состоит в попеременном приставлении к тренируемым глазам на определенное время положительных сферо – призматических элементов различной сферической и призматической диоптрийности.
Графически это выглядит следующим образом:

Используемые материалы
http://traditio-ru.org/wiki/%D0%9F%D1%80%D0%B8%D0%B7%D0%BC%D0%B0_%28%D0%BE%D0%BF%D1%82%D0%B8%D0%BA%D0%B0%29
http://luky.livejournal.com/27090.html
http://www.bakupages.com/blg-list.php?blg_id=3&id=91497&cmm_id=939&usp_id=0
http://www.stroynote.com.ua/news/stroy/yugnaya-koreya-sobiraetsya-udivity-mir-ocherednym-arhitekturnym-chudom.html
http://www.archfacade.ru/2009/02/turning-torso.html
http://mnogogranniki.ru/stati/145-aleksandrijskij-mayak
http://maxfavorit.ru/ekaterinburg-s-vysoty-krysh-2011.htm
http://bokeh.com.ua/articles/213_ispolzovanie_prizmy_dlya_tvorcheskix_fotoeffektov
http://eyecenter.com.ua/doctor/prizma/06.htm
http://tehnika.vperedi.ru/archives/95