Содержание
- 2. Для доказательства того, что задача не имеет решения, Эйлер обозначил каждую часть суши точкой (вершиной), а
- 3. Для знакомства с понятием графа рассмотрим несколько наглядных задач. Задача 1. В государстве Морляндия находятся 8
- 4. Граф - это множество точек или вершин и множество линий или ребер, соединяющих между собой все
- 5. Петля это дуга, начальная и конечная вершина которой совпадают. Пустым (нулевым)называется граф без ребер. Полным называется
- 6. Нулевой граф Граф, состоящий из «изолированных» вершин, называется нулевым графом Рис. 2. Нулевой граф
- 7. Неполный граф Графы, в которых не построены все возможные ребра, называются неполными графами. Рис. 3. Неполный
- 8. Степень графа Количество рёбер, выходящих из вершины графа, называется степенью вершины. Вершина графа, имеющая нечётную степень,
- 9. Заметим, что если полный граф имеет n вершин, то количество ребер равно n(n-1)/2 Задание 1. Существует
- 10. Примеры полных графов Задание 2.Построить полный граф для 5 вершин.
- 11. Ориентированный граф Граф называется ориентированным (или орграфом), если некоторые ребра имеют направление. Это означает, что в
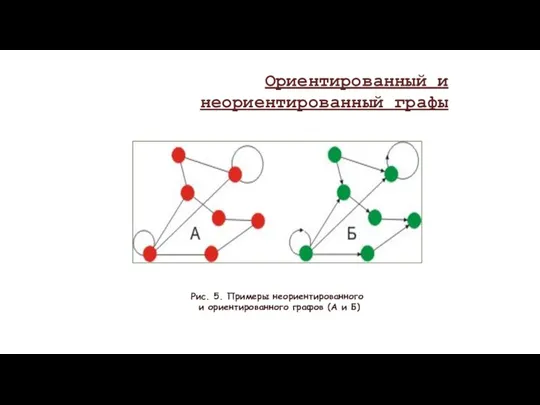
- 12. Рис. 5. Примеры неориентированного и ориентированного графов (А и Б) Ориентированный и неориентированный графы
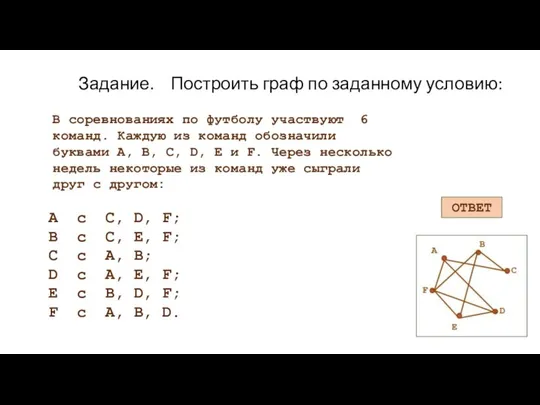
- 13. Задание. Построить граф по заданному условию: В соревнованиях по футболу участвуют 6 команд. Каждую из команд
- 14. Не следует путать изображение графа с собственно графом (абстрактной структурой), поскольку одному графу можно сопоставить не
- 15. Изображение графа Один и тот же граф может выглядеть на рисунках по-разному. На рисунке 6 (а,
- 16. Задание 4. Определить изображают ли фигуры на рисунке один и тот же граф или нет. 1)
- 17. Путём в графе называется такая последовательность ребер, в которой каждые два соседних ребра имеют общую вершину
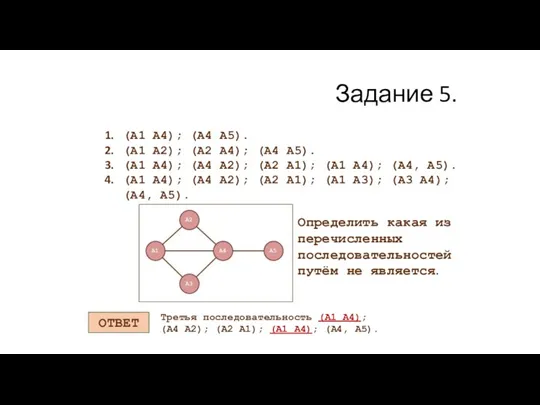
- 18. Задание 5. (А1 А4); (А4 А5). (А1 А2); (А2 А4); (А4 А5). (А1 А4); (А4 А2);
- 19. Путь называется простым, если он не проходит ни через одну из вершин графа более одного раза.
- 20. Понятие цикла в графе Циклом называется путь, в котором совпадают его начальная и конечная вершины. Простым
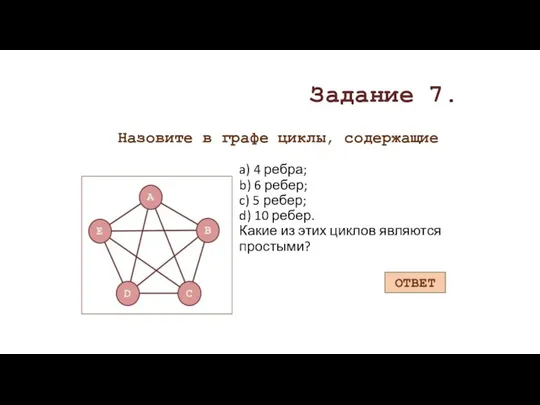
- 21. a) 4 ребра; b) 6 ребер; c) 5 ребер; d) 10 ребер. Какие из этих циклов
- 22. ОТВЕТ (AB, BC, CE, EA), (CD, DA, AB, BC), (EB, BC, CD, DE) и т.д. –
- 23. Теория графов нашла свое применение и в архитектуре и строительстве. При составлении больших проектов, содержащих различные
- 25. Скачать презентацию


















 Построение треугольников по трем элементам
Построение треугольников по трем элементам Математическая статистика
Математическая статистика Параллельные и перпендикулярные прямые
Параллельные и перпендикулярные прямые ОГЭ. Приемы решения практикоориентированных задач
ОГЭ. Приемы решения практикоориентированных задач Сумма углов треугольника
Сумма углов треугольника Повторение. Числа от 100 до 1000 (Урок 1)
Повторение. Числа от 100 до 1000 (Урок 1) Случайные величины
Случайные величины Линейные неравенства. 8 класс
Линейные неравенства. 8 класс Учимся писать цифры
Учимся писать цифры Решение уравнений
Решение уравнений Презентация на тему Математическая мозаика
Презентация на тему Математическая мозаика  Сложение чисел
Сложение чисел Презентация на тему Решение диофантовых уравнений
Презентация на тему Решение диофантовых уравнений  Задачи на координатной плоскости
Задачи на координатной плоскости У мольберта - математик
У мольберта - математик Презентация на тему Понятие площади фигуры и ее измерение
Презентация на тему Понятие площади фигуры и ее измерение  Коллекция игр. 1 класс
Коллекция игр. 1 класс Razonamiento. Matemático práctica
Razonamiento. Matemático práctica Величины
Величины Неопределенный интеграл Ч2, свойства неопределенного интеграла
Неопределенный интеграл Ч2, свойства неопределенного интеграла Уравнение. Решение уравнений способом подбора. Математика, 2 класс
Уравнение. Решение уравнений способом подбора. Математика, 2 класс Основные тригонометрические тождества
Основные тригонометрические тождества Формула Бернулли
Формула Бернулли Моменты случайной величины
Моменты случайной величины Цифровые средства измерения
Цифровые средства измерения Формулы сокращенного умножения. Тренажер
Формулы сокращенного умножения. Тренажер Определитель 3 порядка
Определитель 3 порядка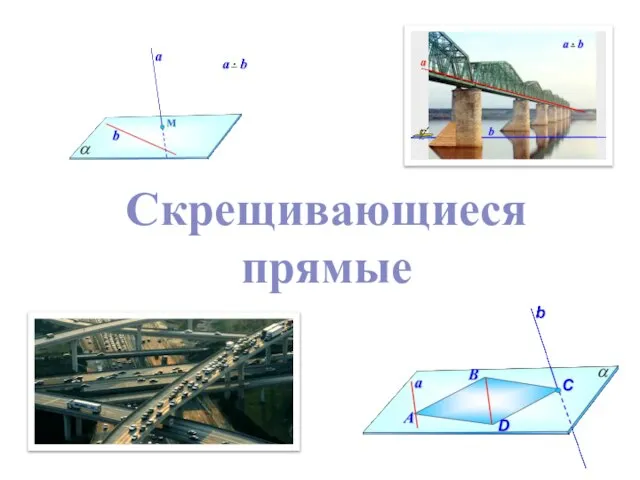 Скрещивающиеся прямые
Скрещивающиеся прямые