Содержание
- 2. Всякое учение истинно в том, что оно утверждает, и ложно в том, что оно отрицает или
- 3. Разминка перед восхождением. Найти первообразную для каждой функции.
- 4. Проверка снаряжения 10) F(x) = 5sin x- 3x2+6 +c
- 5. АЛГОРИТМ РЕШЕНИЕ ЗАДАЧ Построить графики данных линий. Определить искомую фигуру. Найти пределы интегрирования. Записать площадь искомой
- 6. ОСНОВНЫЕ СЛУЧАИ РАСПОЛОЖЕНИЯ ПЛОСКОЙ ФИГУРЫ И СООТВЕТСТВУЮЩИЕ ФОРМУЛЫ ПЛОЩАДЕЙ
- 7. Начало пути "связки А" и "связки В". Найти площадь фигуры, ограниченной линиями. I вариант II вариант
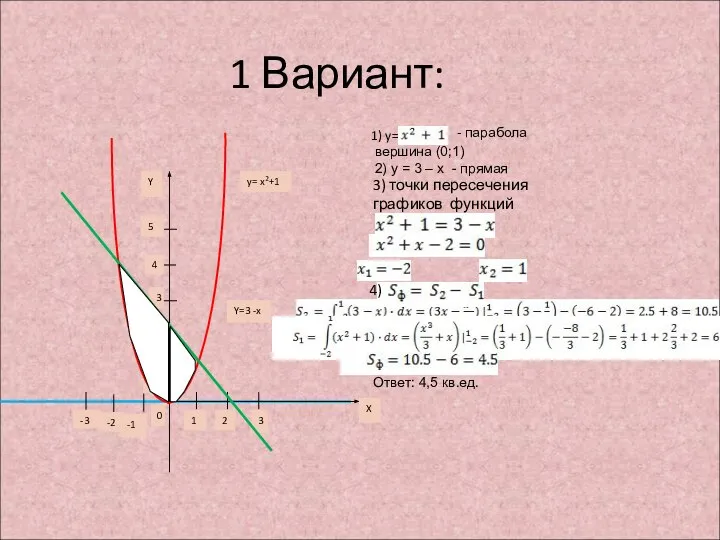
- 8. 1 Вариант: 1 3 2 -1 -2 -3 0 1 4 3 2 5 Y X
- 9. 1 -1 0 2 -2 1 2 x y 2 Вариант: y = 1 – x
- 10. Штурм горы.
- 11. Решение примеров.
- 12. Б А Привал .
- 13. Немного истории «Интеграл» - латинское слово integro – “восстанавливать” или integer – “целый”. Одно из основных
- 14. Немного истории Знак ∫ - стилизованная буква S от латинского слова summa – “сумма”. Впервые появился
- 15. Применение интеграла Площадь фигуры Объем тела вращения Работа электрического заряда Работа переменной силы Центр масс Формула
- 17. Скачать презентацию













 Модуль числа (часть 2)
Модуль числа (часть 2) Второй признак равенства треугольников по стороне и двум прилежащим к ней углам
Второй признак равенства треугольников по стороне и двум прилежащим к ней углам Пространственные и временные представления
Пространственные и временные представления Построение графика квадратичной функции
Построение графика квадратичной функции Методика проверки и оценки алгебраических заданий повышенного уровня сложности
Методика проверки и оценки алгебраических заданий повышенного уровня сложности Теория погрешностей
Теория погрешностей Презентация на тему Задачи на движение для учителя
Презентация на тему Задачи на движение для учителя  Презентация на тему Устный счет по математике
Презентация на тему Устный счет по математике  Пирамиды
Пирамиды Презентация по математике "Что такое понятие" -
Презентация по математике "Что такое понятие" -  Дискретная математика
Дискретная математика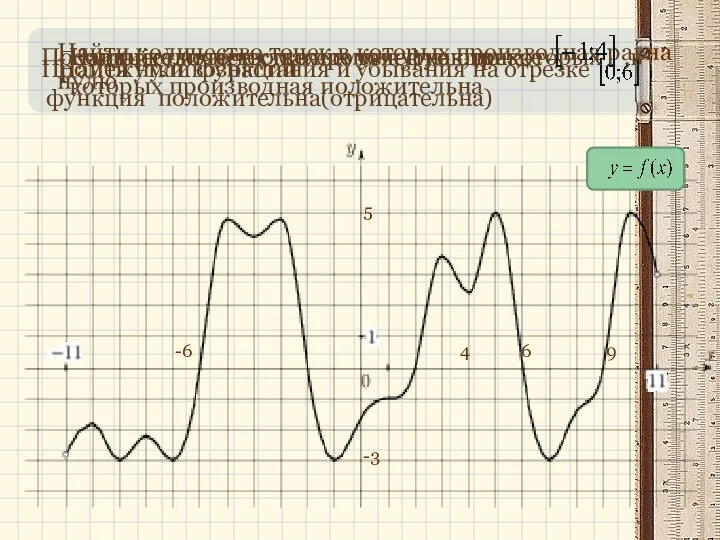 Алгоритм нахождения интервалов выпуклости и точек перегиба
Алгоритм нахождения интервалов выпуклости и точек перегиба Свойства функции
Свойства функции Определение производной. Физический смысл производной
Определение производной. Физический смысл производной Графический диктант Раскрытие скобок
Графический диктант Раскрытие скобок Презентация на тему Подготовка к контрольной работе по алгебре
Презентация на тему Подготовка к контрольной работе по алгебре  Произведение вектора на число
Произведение вектора на число Длина окружности. Площадь круга
Длина окружности. Площадь круга Свойства параллельных прямых. Решение задач
Свойства параллельных прямых. Решение задач Элементы комбинаторики
Элементы комбинаторики Умножение десятичной дроби на десятичную дробь
Умножение десятичной дроби на десятичную дробь Математическая модель
Математическая модель Периодичность синуса и косинуса y = sin x; у = cos x
Периодичность синуса и косинуса y = sin x; у = cos x Регулятивные удд
Регулятивные удд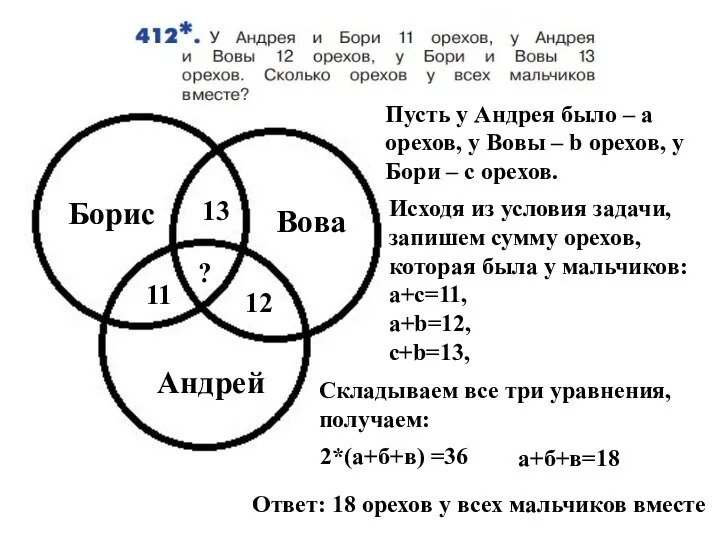 Уравнения. Задача
Уравнения. Задача Выборочное наблюдение. Практическое занятие
Выборочное наблюдение. Практическое занятие Законы умножения для обыкновенных дробей. 5 класс
Законы умножения для обыкновенных дробей. 5 класс Сумма углов треугольника. Виды треугольников
Сумма углов треугольника. Виды треугольников