Численные методы решения СЛАУ (часть 1)

План
Постановка задачи
Классификация методов решения СЛАУ
Прямые методы:
Метод Крамера
Метод Гаусса
Метод Жордана – Гаусса
Модификации методов исключения неизвестных
Камиль Мари Эдмон Жордан (Jordan)
Габриэль Крамер (Cramer)

Постановка задачи
К решению задач линейной алгебры приводит анализ физических систем различной природы: механических, гидравлических, электростатических и т.п.
Системы линейных алгебраических уравнений (СЛАУ) возникают при обработке данных; дискретизации линейных дифференциальных задач; решении краевых задач; расчете электрических цепей; в экономических моделях и т.д.

Постановка задачи
Дана система n линейных алгебраических уравнений с
n неизвестными:
(1)

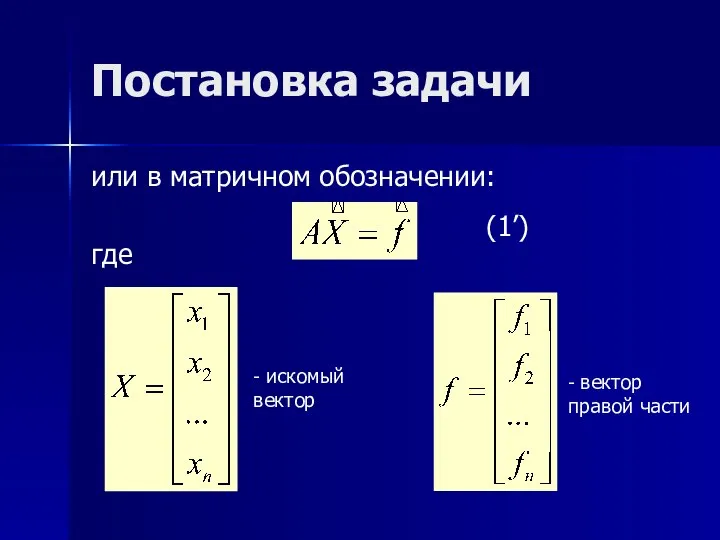
Постановка задачи
или в матричном обозначении:
где
(1’)
- искомый вектор
- вектор правой части

Постановка задачи
Как известно из курса линейной алгебры, если матрица A невырожденная, т.е.
то система (1) имеет единственное решение:

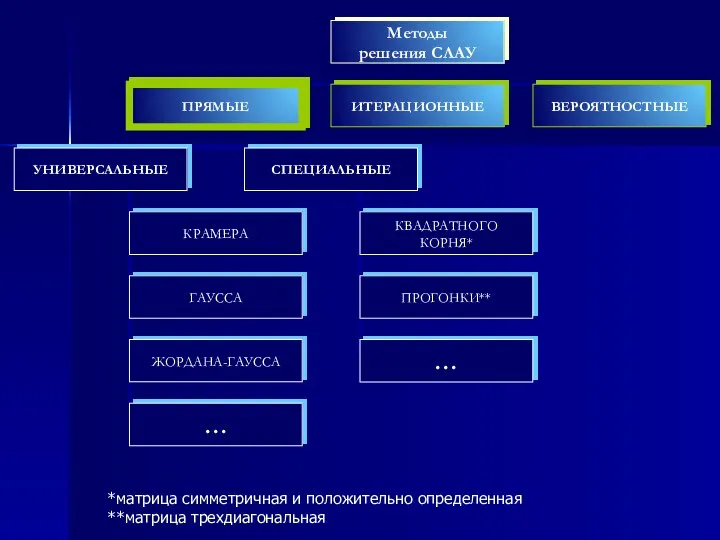
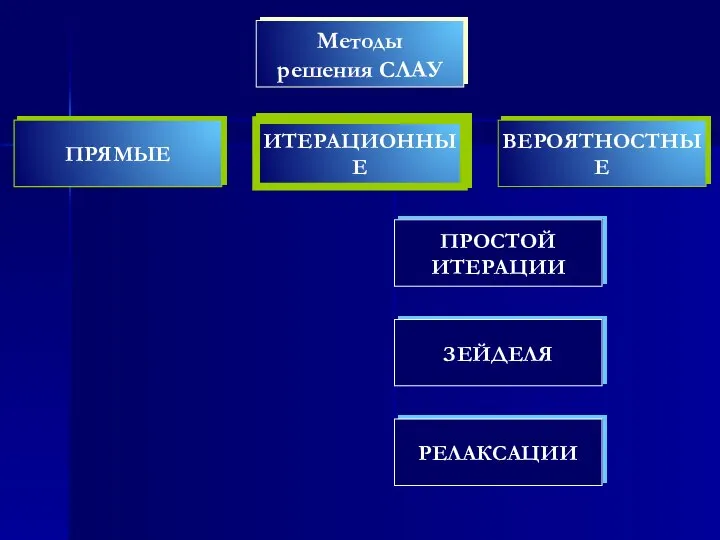
Прямые (точные) методы: решение находится за конечное число арифметических действий. Точными их можно назвать лишь абстрагируясь от погрешностей округления.
Итерационные методы состоят в том, что решение системы (1) определяется как предел некоторой последовательности приближений X k при k→∞, где k – номер итерации.
Вероятностные методы или методы Монте-Карло используют для решения систем с очень большим числом неизвестных (>107).
Методы решения СЛАУ

*матрица симметричная и положительно определенная
**матрица трехдиагональная

Метод Крамера
Универсальным прямым методом решения систем вида (1), известным из курса алгебры, является метод Крамера:
Для реализации на ЭВМ этого метода необходимо выполнить - умножений для каждого определителя. Подобным способом можно пользоваться, если n невелико
(обычно< 5), в противном же случае такой метод становится очень затратным.

Пример. Метод Крамера

Метод Гаусса
Запишем систему (1) в виде:
Предположим, что , если иначе, то переставим строки.
(2)

Прямой ход метода Гаусса
Исключим x1 из n-1 последних уравнений, для этого из второго уравнения вычтем первое, умноженное на
Из третьего вычтем первое умноженное на
и т.д.

Прямой ход метода Гаусса
Этот процесс приведет к системе:
При исключении x1 преобразованию подвергаются строки расширенной матрицы, включая свободные члены.
(3)

Прямой ход метода Гаусса
Если , то применим аналогичный процесс к последующим уравнениям и исключим x2 из n-2 уравнений.

Прямой ход метода Гаусса
k – тый шаг

Прямой ход метода Гаусса
Выпишем в общем виде рекуррентные соотношения для получения коэффициентов матрицы на k -м шаге:

Смысл индексов
k – номер того уравнения, которое вычитается из остальных и номер того неизвестного, которое исключается из последующих уравнений;
- называется
разрешающим элементом;
i – номер уравнения из которого в данный момент исключается неизвестное;
j – текущий номер столбца.

Прямой ход метода Гаусса
Через n-1 шаг система будет приведена к треугольному виду, при этом прямой ход метода Гаусса завершен.
Схематическая иллюстрация прямого хода метода Гаусса

Обратный ход метода Гаусса
Осуществляется для нахождения неизвестных системы.
Из последнего уравнения находится xn. Его значение подставляется в n-1 уравнение …
и т. д. до первого уравнения и х1.

Обратный ход
Искомое решение системы (1) определяется по формулам:
Весь алгоритм метода Гаусса осуществляется за порядка арифметических операций.

Пример. Метод Гаусса
Методом Гаусса решить систему уравнений:

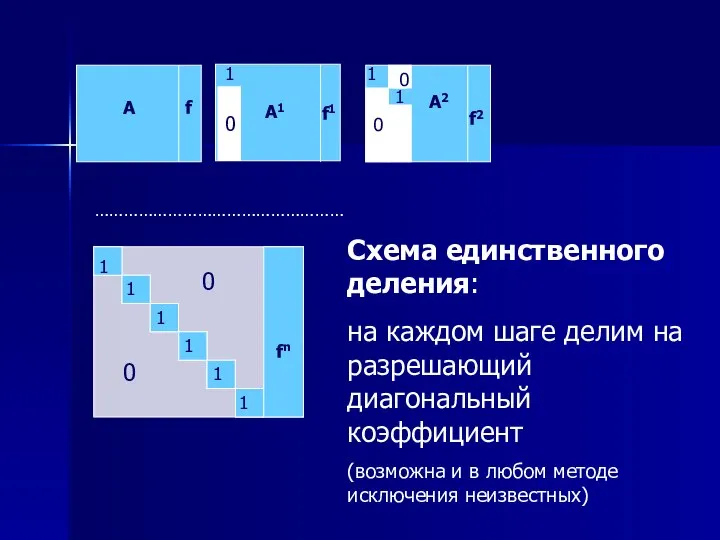
Пример. Метод Гаусса (со схемой единственного деления*)
* Схема единственного деления применяется для получения 1 на диагонали путем деления на разрешающий элемент

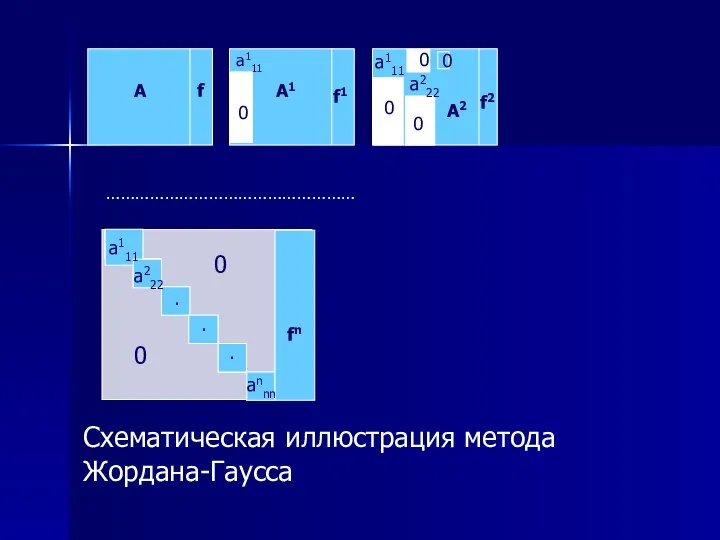
Метод Жордана – Гаусса
Идея модификации метода Гаусса состоит в том, чтобы одновременно осуществить прямой и обратный ход, приведя исходную матрицу к диагональному виду.
Если при этом на главной диагонали будут 1, то искомое решение – вектор свободных членов. Схематически метод выглядит следующим образом:

Схематическая иллюстрация метода Жордана-Гаусса
0
annn
0

Метод Жордана – Гаусса

Модификации методов исключения неизвестных
Схема единственного деления
Выбор главного элемента

0
Схема единственного деления:
на каждом шаге делим на разрешающий диагональный коэффициент
(возможна и в любом методе исключения неизвестных)

Пример. Метод Жордана-Гаусса (схема единственного деления)

Выбор главного элемента
Пример. Дана система
Точным решением данной системы является вектор (0,-1,1).

Выбор главного элемента
Проведём преобразования системы по методу Гаусса, округляя промежуточные результаты до 5 значащих цифр.

Прямой ход

Обратный ход

Сильная потеря точности связана с выбором на 2-м шаге разрешающего элемента Из-за ограниченной точности вычислений (5 значащих цифр) допущена большая относительная погрешность, которая распространяется далее на все вычисления.
Этот пример иллюстрирует следующую ситуацию: если на k-ом шаге диагональный элемент не равен нулю, но его значение мало (≈ε), то, может быть, этот элемент ≠0 только из-за ошибок округления, а должен быть 0 и делить на него нельзя.

Чтобы исключить подобное, алгоритм метода исключения неизвестных модифицируется. На каждом шаге с помощью перестановки строк в качестве разрешающего подбирается наибольший по модулю из возможных элемент. Такая модификация носит название выбор главного элемента.

В рассмотренном примере выбор главного элемента осуществляется следующим образом:
переставим 2-ое и 3-е уравнения:
исключим х2 из 3-го уравнения:

Обратный ход
Результат совпадает с точным решением.