lecture5

Определение: Вероятностный автомат
[англ., probabilistic automat) (ВА)
- это дискретный потактный преобразователь информации с памятью, функционирование которого в каждом такте зависит только от состояния памяти нем и может быть описано статистически.
P-схемы

в проектировании дискретных систем, проявляющих статистически закономерное случайное поведение;
в определении алгоритмических возможностей систем;
в обосновании границ целесообразности их использования;
в решении задач синтеза по выбранному критерию дискретных стохастических систем, удовлетворяющих заданным ограничениям.
Схемы вероятностных автоматов применяются:
P-схемы

Пусть множество G, элементами которого являются всевозможные пары где xi и zs — элементы входного подмножества X и подмножества состояний Z соответственно . Если существуют две такие функции и ,то с их помощью осуществляются отображения и , то говорят, что (1) определяет конечный автомат детерминированного типа.
Математическое понятие Р-автомата формируется на понятиях, введенных для
F-автомата.
P-схемы

Введем более общую математическую схему. Пусть Ф — множество всевозможных пар вида (zk, yj), где
yj — элемент выходного подмножества Y,т.е.
Пусть в любой элемент множества G индуцирует на множестве Ф некоторый закон распределения следующего вида:
P-схемы

P-схемы
Таблица 1. Закон распределения

При этом , (2) где bkj — вероятности перехода автомат в состояние zk и выдаче на выходе сигнала yj, если автомат был в состоянии z.S, и на его вход в момент времени поступил сигнал хi.
Число таких распределений, представленных в виде таблиц, равно числу элементов множества G.
P-схемы
Обозначим множество этих таблиц через В. Тогда четверка элементов (3) называется
вероятностным автоматом (Р-автоматом).

Пусть элементы множества G индуцируют некоторые законы распределения на подмножествах Y и Z, которые можно представить соответственно в виде:
P-схемы
Вероятностный автомат Мили

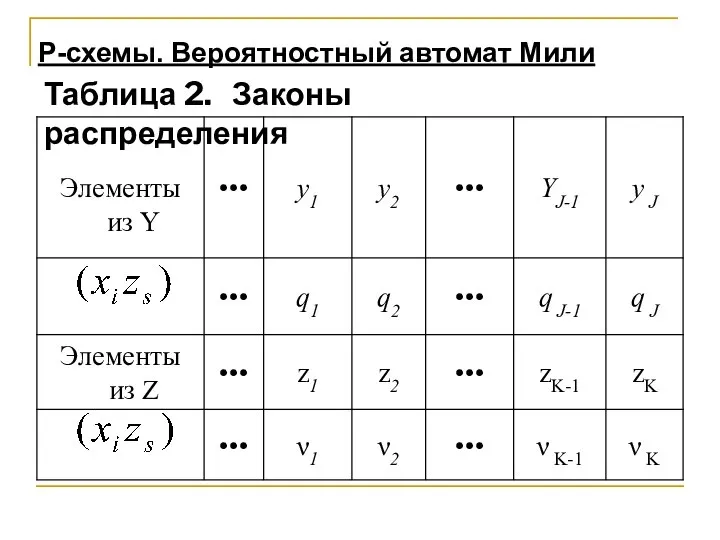
P-схемы. Вероятностный автомат Мили
Таблица 2. Законы распределения

При этом и (4)— вероятности перехода Р-автомата в состояние zk и выдачи выходного сигнала yk при условии, что Р-автомат находился в состоянии zS и на его вход поступил входной сигнал xt.
P-схемы. Вероятностный автомат Мили

Если для всех k и j имеет место соотношение (5), то такой автомат называется вероятностным автоматом Мили. Представленное требование означает выполнение условия независимости распределений для нового состояния Р-автомата и его выходного сигнала.
P-схемы. Вероятностный автомат Мили

Пусть выходной сигнал Р-автомата зависит лишь от того состояния, в котором находится автомат в данном такте работы, каждый элемент выходного подмножества Y индуцирует распределение вероятностей выходов, имеющее следующий вид:
Вероятностный автомат Мура

P-схемы. Вероятностный автомат Мура
Таблица 3. Распределение вероятностей

Здесь ,(6) где Si, — вероятность появления сигнала на выходе yi при условии, что Р-автомат находился в состоянии zk.
P-схемы. Вероятностный автомат Мура

Частным случаем Р-автомата являются автоматы, у которых либо переход в новое состояние, либо выходной сигнал определяются детерминировано. Такой автомат называется
Y-детерминированным вероятностным автоматом.
P-схемы. Вероятностный автомат Мура

Если состояние Р-автомата определяется детерминировано, то такой автомат называется Z-детерминированным вероятностным автоматом.
Аналогично, Z-детерминированным вероятностным автоматом называется
Р-автомат, у которого выбор нового состояния является детерминированным.
P-схемы. Вероятностный автомат Мура

Пусть У-детерминированный Р-автомат,
задан таблицей переходов : где pij – вероятность перехода автомата из состояния zi в состояние zj Можем записать (7)
Рассмотрим пример
У-детерминированного Р-автомата

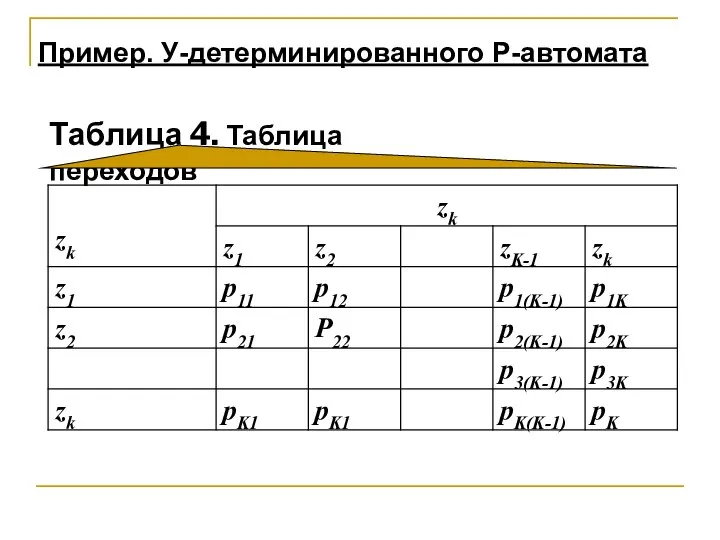
Пример. У-детерминированного Р-автомата
Таблица 4. Таблица переходов

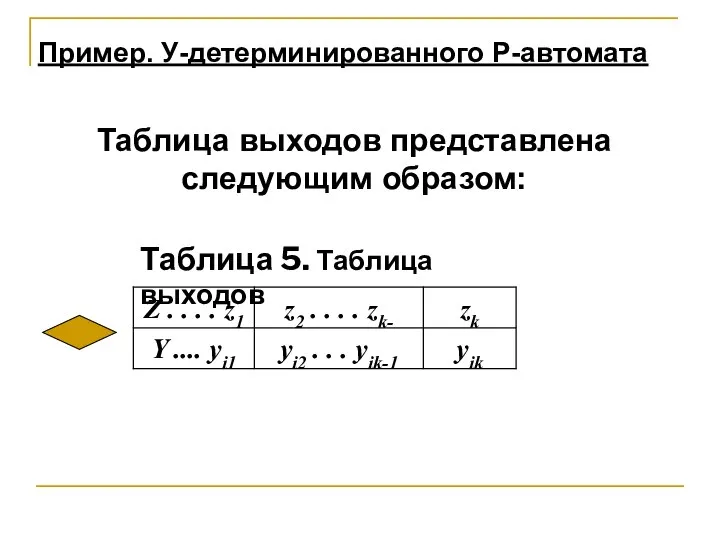
Таблица выходов представлена следующим образом:
Пример. У-детерминированного Р-автомата
Таблица 5. Таблица выходов

Первую из этих таблиц можно представить в виде квадратной матрицы размерности
К x К, которая называется матрицей переходных вероятностей или просто матрицей переходов Р-автомата. В общем случае матрица переходов имеет вид
(8)
Пример. У-детерминированного Р-автомата

Для полного описания У-детерминированного
Р-автомата необходимо задать начальное распределение вероятностей вида
где dK — вероятность того, что в начале работы автомат находится в состоянии zk
При этом . (9)
Пример. У-детерминированного Р-автомата
Таблица 6. Распределение вероятностей

Будем предполагать, что до начала работы (до нулевого такта времени) Р-автомат всегда находится в состоянии z0, в нулевом такте времени меняет свое состояние в соответствии с распределением D. Дальнейшая смена состояний Р-автомата определяется матрицей переходов РР.
Пример. У-детерминированного Р-автомата

- сопоставляется со
состоянием z0 (11)
Информацию о начальном состоянии
Р-автомата удобно внести в матрицу РР/ , увеличив ее размерность до (10).
При этом первая строка такой матрицы, сопоставляемая состоянию z0, будет иметь вид (0, dt, d2, ... ..., dK), а первый столбец будет нулевым.
Пример. У-детерминированного Р-автомата

Описанный У-детерминированный
Р-автомат можно задать в виде ориентированного графа, вершины которого сопоставляются состояниям автомата, а дуги — возможным переходам из одного состояния в другое.
Дуги имеют веса, соответствующие вероятностям перехода рij, а около вершин графа пишутся значения выходных сигналов, индуцируемых этими состояниями.
Пример. У-детерминированного Р-автомата

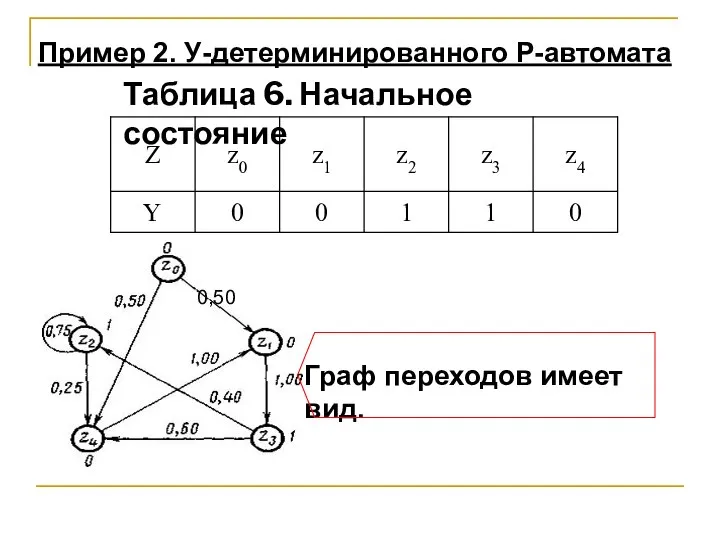
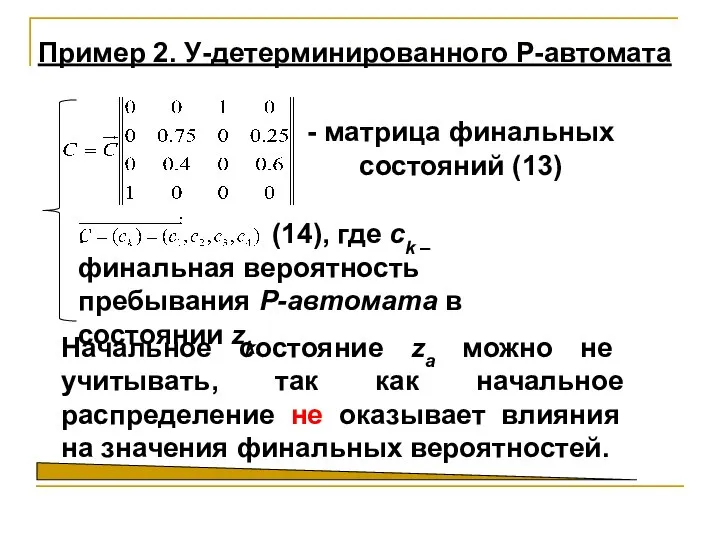
Рассмотрим следующий пример.
У-детерминированный Р-автомат
задан матрицей
Пример 2. У-детерминированного Р-автомата

0,50
Таблица 6. Начальное состояние
Граф переходов имеет вид.
Пример 2. У-детерминированного Р-автомата

Требуется оценить суммарные финальные вероятности пребывания этого Р-автомата в состояниях z2 и z3.
При использовании аналитического подхода можно записать известные соотношения из теории Марковских цепей и получить систему уравнений для определения финальных вероятностей.
Пример 2. У-детерминированного Р-автомата

Начальное состояние za можно не учитывать, так как начальное распределение не оказывает влияния на значения финальных вероятностей.
- матрица финальных состояний (13)
Пример 2. У-детерминированного Р-автомата
. (14), где ck – финальная вероятность пребывания Р-автомата в состоянии zk.

Добавим к этим уравнениям условие нормировки с1 + с2 + с3 + с4 = 1 (16).
Тогда, решая систему уравнений, получим
с1 = 5/23, с2=8/23, c3 = 5/23, с4 = 5/23 (17).
Таким образом, с2+с3= 13/23 =0,5652 (18).
Получаем систему уравнений(15)
Пример 2. У-детерминированного Р-автомата

Другими словами, при бесконечной работе заданного в этом примере
У-детерминированного Р-автомата на его выходе формируется двоичная последовательность с вероятностью появления единицы, равной 0,5652.
Пример 2. У-детерминированного Р-автомата

Подобные Р-автоматы могут использоваться как генераторы Марковских последовательностей, которые необходимы при построении и реализации процессов функционирования систем S или воздействий внешней среды Е.
Пример 2. У-детерминированного Р-автомата